铜基复合材料具有良好的力学、导电、导热性能，在电子工业、机械制造、航天航空、国防电气等领域应用广泛[1-3]。随着行业领域的快速发展，人们对铜基复合材料的性能和使用提出了更高的要求，开发高强度和高导电性的铜基复合材料成为重要研究方向[4-6]。
通过添加具有高强度、高硬度的TiB 和TiB2 陶瓷增强相，可以大大提高铜基复合材料性能[7]。然而，复合材料的高强度和高导电率存在矛盾关系，获得高强度的同时，其导电率必然降低[8]。同时，由于TiB 和TiB2 陶瓷增强相特征参量交互、协同影响铜基复合材料各项性能，单纯依赖实验手段难以全面揭示各特征参量对复合材料的具体影响，无法获取综合性能极佳的铜基复合材料[9-10]。如何定量评价TiB和TiB2 陶瓷增强相及二者混杂占比特征等对铜基复合材料强度和导电率的具体影响，对于高性能铜基复合材料的设计开发具有重要意义。
传统铜基复合材料研究按照理论分析、仿真建模、拓扑优化等思路展开，主要进行科学实验和数值模拟，实验周期长、成本高，结果不稳定，易受异常情况的影响，分析方法也较为受限，难以全面表征增强相特征与性能间未知复杂关系[11-13]。随着机器学习、深度神经网络等技术不断发展，数据赋能传统数学、力学和实验模型的思想逐步得到应用。通过确定正确的目标函数、模型结构，基于当前实验数据，不断迭代训练，学习特征与性能间关系，可构建预测模型，应用于复合材料性能设计和结构优化。
BP(back propagation)神经网络具有良好的非线性映射、泛化和容错能力，是目前应用较为广泛的人工神经网络[14]。蚁群算法[15]是一种仿生智能优化算法，常用于求解组合优化、路径规划等问题，其灵感来源于蚂蚁觅食的过程，蚂蚁在寻找食物源的路径上会留下信息素，而群体内的蚂蚁可以感知信息素，并沿着信息素浓度高的地方移动，形成正反馈机制，经过一段时间之后，蚂蚁就可以确定一条到达食物源的最优路径。本文基于机器学习算法，针对网络隐含层节点设置问题，引入蚁群算法动态寻优确定BP 神经网络隐含层结构，建立基于蚁群算法优化的BP 神经网络铜基复合材料力电性能预测模型。考察TiB 和TiB2 陶瓷增强相对铜基复合材料力学性能和导电性能的影响规律，为高强高导铜基复合材料制备提供理论依据。
1 模型构建
1.1 问题描述
给定训练数据集D={(xk,yk)}(k=1,2,…,K)，其中xk∈R2 表示输入数据，包括TiB 晶须体积、TiB2颗粒体积2 个特征，yk∈R1 表示模型输出数据，包括铜基复合材料的导电率(EC)、屈服强度(YS)、拉伸强度(TS)、伸长率(EL)4 项性能，K 表示实验样本数量。旨在建立基于蚁群算法优化的BP 神经网络铜基复合材料性能预测模型，模拟TiB 和TiB2 陶瓷增强相对铜基复合材料性能的影响。
1.2 模型构建
输入训练数据，以蚁群算法搜索到的隐含层节点数量构建BP 神经网络并进行训练测试，计算每组TiB 和TiB2 陶瓷增强相参数组合所对应实际输出和期望输出的误差，找到最小误差，更新蚁群信息素，并反复迭代，直至模型收敛，得到(TiB2+TiB)/Cu铜基复合材料性能预测模型，流程如图1 所示。
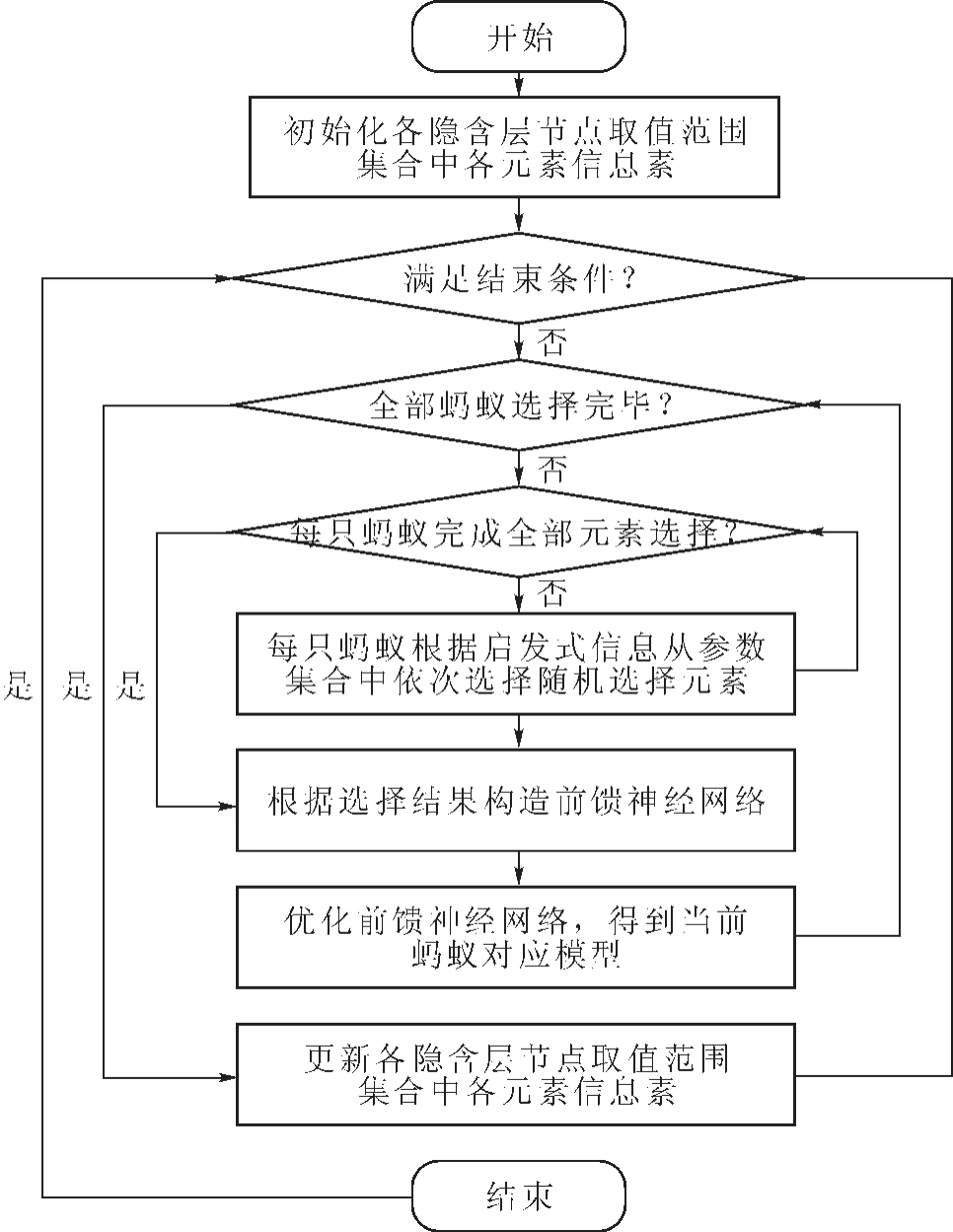
图1 模型流程图Fig.1 Model flowchart
步骤1：初始化。设置BP 神经网络的隐含层数L，被优化的各隐含层节点取值范围集合Si(i=1,2,…,L)，集合Si 中的元素个数Qi，最大迭代次数Nbp-max。设置蚁群算法最大迭代次数为Naco-max，蚂蚁数量M，局部搜索步长step。
步骤2：随机产生蚂蚁初始位置，计算适应度函数值，设为蚁群算法初始信息素，并计算状态转移概率Pn。
式中，τmax 为信息素的最大值；τm 为蚂蚁的信息素；Pn为第n 次迭代蚂蚁m 的转移概率。然后，进行蚁群方案更新。
当状态转移概率小于转移概率常数时，进行局部搜索。
式中，solutionnew 为蚂蚁生成的新的解空间；solutionold 为蚂蚁原先的解空间；r1 为介于[-1,1]的随机数；step 为局部搜索步长；
为当前迭代次数的倒数。当状态转移概率大于转移概率时，进行全局搜索。
式中，r2 为[-0.5,0.5]的随机数；range 为隐含层节点个数的区间大小。
步骤3：以每只蚂蚁选择的解空间为隐含层节点个数构造多层BP 神经网络，利用前馈算法对BP神经网络进行训练，使用实际输出和期望输出的均方误差MSEij 作为损失函数。
式中，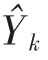
为网络实际输出；Yk 为网络期望输出。对训练结束后的均方误差进行排序，找到最小误差，对应的蚂蚁即为本次迭代最优解。通过判断待移动位置损失与当前位置损失的大小来确定是否更新蚂蚁当前位置，并利用边界吸收方式进行边界条件处理，将蚂蚁位置界定在取值范围内。
步骤4：根据本次迭代解损失对蚁群算法信息素进行更新。
式中，τij(t)为t 时刻元素sij 的信息素浓度；τij(t+1)为更新后t+1 时刻元素sij 的信息素浓度；
为蚂蚁m 本次循环中在元素sij 上留下的信息量；Δτij(t)为在本次循环结束后，所有蚂蚁在元素sij 上留下的总信息素量；Q 为常数，用于控制蚁群算法收敛速度，Q 值越小，蚁群算法收敛速度越慢，反之，蚁群算法收敛速度越快。当蚁群算法的迭代次数Naco-max 满足最大迭代次数，结束循环，输出最优解对应网络结构作为(TiB2+TiB)/Cu 铜基复合材料性能预测模型ACO-BP-Cu，同时根据测试数据输出预测结果。模型对应伪代码如表1 所示。
表1 模型伪代码
Tab.1 Pseudo-code of the proposed model
2 实验方法
2.1 实验环境与数据集
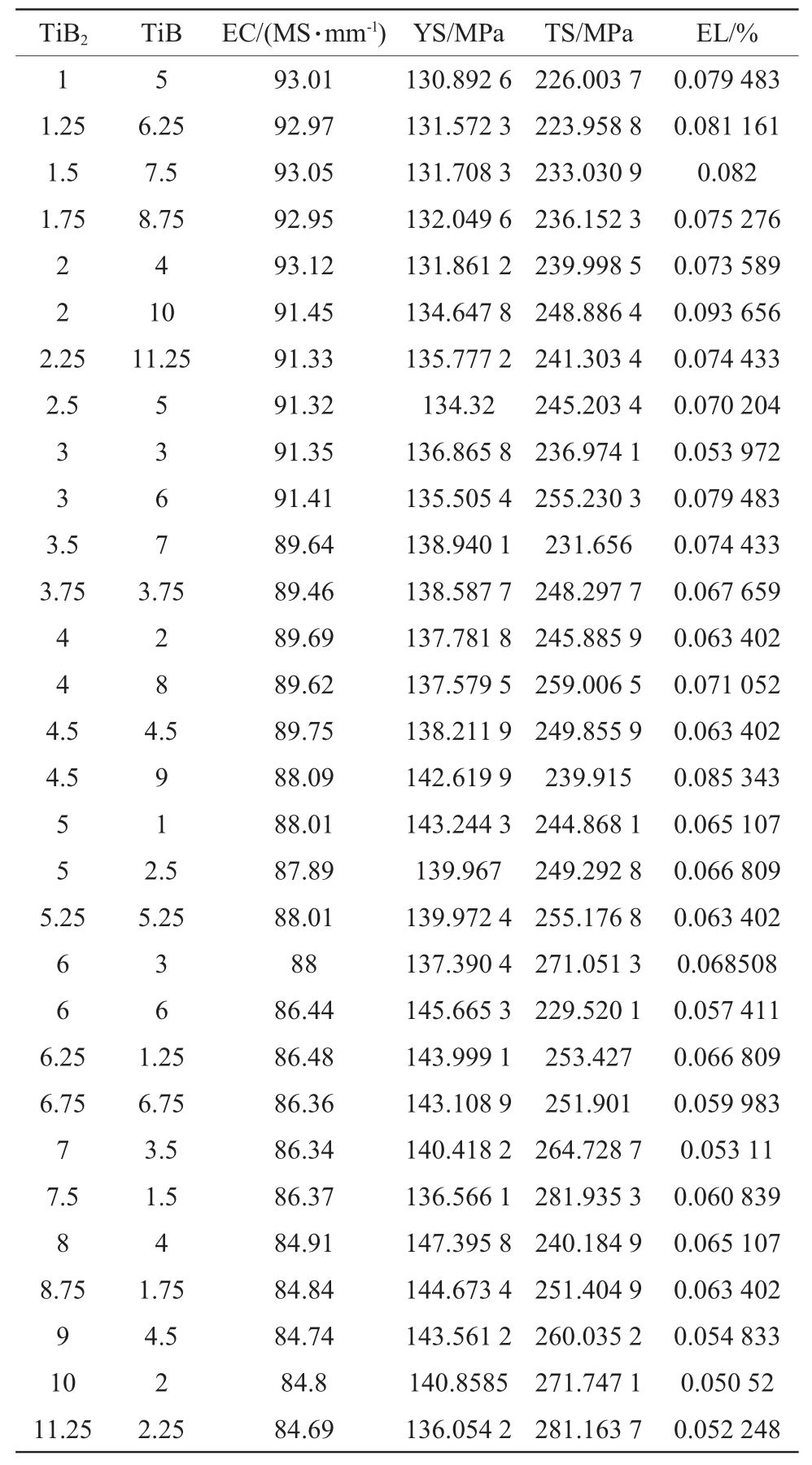
在真实数据集上进行对比实验验证所提模型的有效性及优越性。程序语言为python-3.6.13，使用keras-2.3.0、scikit-learn-0.24.2 实现相关算法，CPU为11th Gen Intel(R)Core(TM)i7-11800H@2.30 GHz 2.30 GHz，内存为16G，显卡为NVIDIA GeForce RTX3070，操作系统为Windows 11。实验数据来源于(TiB2+TiB)/Cu 有限元模型[16]。数据集自变量为电子显微镜获得的TiB2 颗粒和TiB 晶须几何特征，因变量为加入相应配比的TiB2 颗粒和TiB 晶须后，得到的铜基复合材料导电率EC(MS/mm)、屈服强度YS(MPa)、拉伸强度TS(MPa)和伸长率EL(%)4 项性能，共30 个样本，信息如表2 所示。
表2 实验数据集
Tab.2 Datasets
2.2 评价指标
由于所提模型总体为回归预测模型[17]，而R2 指标由于能够很好表征观测值和预测值之间的差异，反映模型的可靠性和效果，在回归预测领域被作为评价指标广泛使用，R2 通过下式表示：
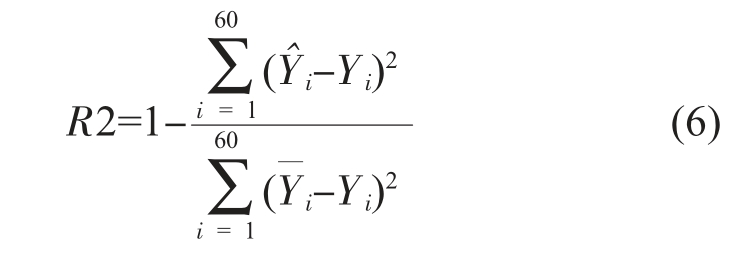
式中，(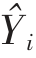
-Yi)2 为真实值与预测值的平方差；(
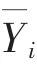-Yi)2 为真实值与均值的平方差。系数R2 常规取值范围为0～1，值越大，模型拟合效果越好；若R2 取值为负数，则模型无效。
2.3 数据分析
为了初步掌握TiB2 颗粒和TiB 晶须的几何特征与铜基复合材料导电率、屈服强度、拉伸强度和伸长率4 项性能的相关性及数据分布特征规律，进行特征间Pearson 相关性[18]分析，并绘制样本相关性散点图，结果如图2 所示。图2 中红色为正相关，蓝色为负相关，圆形大小与Pearson 相关系数保持一致，在圆心处标识。
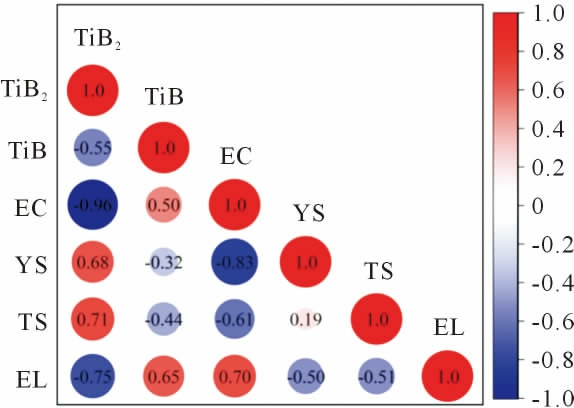
图2 相关性分析结果
Fig.2 Correlation analysis results
由图2 可知，TiB2 颗粒和TiB 晶须的几何特征与4 项性能及性能本身存在不同程度的线性相关，其中TiB2 颗粒体积与导电率与伸长率、导电率与屈服强度相关性大于0.7，为高度线性相关。当同时调整TiB2 颗粒、TiB 晶须配比，相应性能分布是否仍然服从此规律，无法通过简单函数直接表示，有必要分别建立回归模型，表征铜基复合材料各项性能与特征参数之间的复杂关系。
2.4 对比实验
为了验证所提算法的优越性，将所提算法分别与决策树(decision tree,DT)、随机森林(random forest,RF)、引导聚集算法(bootstrap aggregating,BA)、梯度提升决策树(gradient boosting decision tree,GBDT)、自适应增强决策树(adaptive boosting decision tree,ABDT)、线性回归(linear regression,LR)、支持向 量回归(support vector regression,SVR)、K 邻近法(K-nearest neighbor,KNN)、极端随机树(extremely randomized trees,ERT)9 种回归算法进行对比。
ACO-BP-Cu 模型训练数据与测试数据按照4∶1划分，根据Dorigo 等[19]给出的蚁群算法参数进行多组实验，确定本模型使用的蚁群算法常数Q 为1，迭代次数为10、蚂蚁数量为5。综合考虑数据规模和模型表现，经过多次优化，确定模型使用的BP 神经网络迭代次数为1 000，学习率为0.01，隐含层层数为2，采用Relu[20]作为激活函数。针对铜基复合材料导电率、屈服强度、拉伸强度和伸长率4 项性能进行训练并预测，蚁群算法最终构造的BP 神经网络隐藏层节点个数如表3 所示。
表3 ACO-BP-Cu最终隐层含节点个数
Tab.3 The number of hidden layer nodes in the final ACO-BP-Cu
对比实验结果如图3 所示，横轴分别为不同对比算法，纵轴为评价指标，不同颜色折线分别表示各回归算法对铜基复合材料不同性能的预测情况。
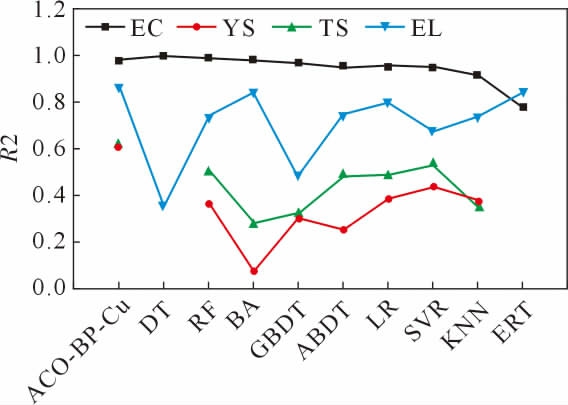
图3 对比实验结果
Fig.3 Results of comparative experiments
从图3 可以看出，部分对比算法R2 指标为负数，代表方法无效。即决策树DT 和极端随机树ERT模型对拉伸强度和屈服强度的预测无效，其余所有回归算法对各项性能预测均有效。ACO-BP-Cu 模型模型在各个性能上预测结果更接近1。同时，各算法对不同性能的预测结果存在波动，效果由好到坏依次为对导电率、屈服强度、拉伸强度、伸长率的预测。不同算法针对不同性能的预测结果也存在差距，这与各性能和增强相间关系有关，当相关关系适用于当前回归模型时，效果相对较好，而ACO-BP-Cu 模型由于具备较好的泛化能力和较强的表达能力，其在各项性能预测上的表现也相对鲁棒。对于YS，ACO-BP-Cu 模型预测结果相对其他性能，效果一般。分析原因为：①训练样本数据有限；②模型还存在进一步优化的空间。但是，通过不同方法间的对比，该模型仍然较其它方法更具优势，且R2 值大于0 接近0.6，也能够说明算法是有效的。我们会在后续的研究中通过增加样本空间数量来进一步提升相关性能的预测水平，使模型更具指导意义。
以导电率预测为例，图4 展示了蚁群算法迭代过程中评价指标的变化，图5 展示了真实值与预测值间的关系。
图4 蚁群算法评价指标变化(以导电率为例)
Fig.4 Ant colony algorithm R2 curve(taking EC as an example)
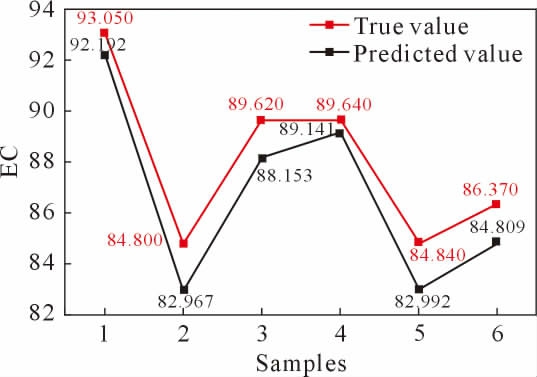
图5 模型预测值导电率与真实导电率
Fig.5 True EC and predicted EC
由图4 可知，随着迭代次数不断增加，评价指标不断上升，大约在迭代10 次之后稳定在0.984，并最终确定了模型的隐含层个数。
由图5 可知，图中每点代表1 个测试数据，对于不同测试数据，预测值与真实值相差不多，总体趋势保持一致，在一定误差范围内，模型能够根据TiB2 颗粒和TiB 晶须两项特征预测铜基复合材料性能。
2.5 学习率敏感性实验
为验证学习率对BP 神经网络结果的影响，以导电率预测为例，将神经网络学习率分别设置为0.000 1,0.001,0.01,0.1 进行实验，图6 展示了评价指标R2 随学习率变化情况。由图6 可知，模型受学习率影响不大，当学习率设置为0.001 或0.01 时效果最优。
图6 学习率对模型导电率预测影响
Fig.6 The influence of the learning rate on EC prediction
3 结论
(1)在预测力学、电学性能时，基于蚁群算法进行动态寻优，确立了BP 神经网络的隐含层节点数量，获得了[36、29]、[23、85]、[75、65]和[83、58]个节点的最优设置。
(2)ACO-BP-Cu 预测模型的结果与其他9 种回归算法(决策树、随机森林、引导聚集算法、梯度提升决策树、自适应增强决策树、线性回归、支持向量回归、K 邻近法和极端随机树)的结果进行对比分析。表明ACO-BP-Cu 预测模型的预测精度显著高于其他算法，在预测不同复合材料力电性能方面，ACO-BP-Cu 预测模型表现出明显的优势。
(3)该模型受学习率影响小，表现出较强的有效性和相对鲁棒性，可进一步拓展到复杂空间构型化铜基复合材料力电性能与特征参数之间映射关系的建立。为具有智能空间构型设计的铜基复合材料制备提供理论依据。
[1]王怡然，高义民.Ti 元素对Ti3SiC2 在铜基复合材料中的分解抑制研究[J].铸造技术，2022,43(6):410-416.WANG Y R,GAO Y M.Effect of Ti in inhibiting the decomposition of Ti3SiC2 in copper matrix composites[J].Foundry Technology,2022,43(6):410-416.
[2]LIU N,ZHANG Q Q,FENG P F,et al.Effects of configuration parameters on the deformation and fracture behaviors of TiB2/Cu composites with network structure:A numerical approach using an enhanced fi nite element model[J].Computational Materials Science,2022,205:111212.
[3]LIU N,ZHANG Q Q,ZHANG H Y,et al.Experimental verification and numerical analysis on plastic deformation and mechanical properties of the in-situ TiB2 homogeneous composites and TiB2/Cu network composites prepared by powder metallurgy[J].Journal of Alloys and Compounds,2022,920:165897.
[4]LIU N,ZHANG X,ZHANG Q Q,et al.Numerical evaluation and experimental verification of mechanical properties and fracture behavior for TiB2/Cu composites prepared by in-situ mixing casting[J].Journal of Alloys and Compounds,2022,895:162475.
[5]李海生，周叶晨，李烨飞，等.烧结温度对MAX/Cu 复合材料的组织及性能影响[J].铸造技术，2022,43(6):439-444.LI H S,ZHOU Y C,LI Y F,et al.Effect of sintering temperature on microstructure and properties of MAX/Cu composites[J].Foundry Technology,2022,43(6):439-444.
[6]帅歌旺，张萌.高强度、高导电铜合金及铜基复合材料研究进展[J].特种铸造及有色合金，2005,25(9):534-537.SHUAI G W,ZHANG M.Progress in high-strength and high-conductivity copper alloys and copper base composites[J].Special Casting&Nonferrous Alloys,2005,25(9):534-537.
[7]WANG J,GUO L N,LIN W M,et al.The effects of graphene content on the corrosion resistance,and electrical,thermal and mechanical properties of graphene/copper composites[J].New Carbon Materials,2019,34(2):161-169.
[8]WANG F C,ZHANG Z H,LUO J,et al.A novel rapid route for in situ synthesizing TiB-TiB2 composites[J].Composites Science and Technology,2009,69(15-16):2682-2687.
[9]GUO X H,YANG Y B,SONG K X,et al.Arc erosion resistance of hybrid copper matrix composites reinforced with CNTs and micro-TiB2 particles[J].Journal of Materials Research and Technology,2021,11:1469-1479.
[10]任建强，梁淑华，姜伊辉，等.原位(TiB2-TiB)/Cu 复合材料组织与性能研究[J].金属学报，2019,55(1):126-132.REN J Q,LIANG S H,JIANG Y H,et al.Research on the microstructure and properties of in situ(TiB2-TiB)/Cu composites[J].Acta Metallurgica Sinica,2019,55(1):126-132.
[11]LIU N,ZHANG X,ZHANG X D,et al.Numerical investigations on the hybrid effect and deformation mechanism of TiB2p and TiBw reinforced Cu composites prepared by in-situ mixing casting[J].Computational Materials Science,2022,213:111657.
[12]曹飞，许英琴，张兴德，等.球形Cu 粉粒径对谐波结构TiB2/Cu复合材料组织及性能的影响[J].铜业工程，2023(5):10-16.CAO F,XU Y Q,ZHANG X D,et al.Microstructure and properties of heterogeneous TiB2/Cu composites based on different spherical Cu particle sizes with a harmonic structure[J].Copper Engineering,2023(5):10-16.
[13]丁昱寰，张修庆，徐金鹏，等.(Ti2SnC+TiB2)颗粒增强铜基复合材料的研究[J].热加工工艺,2015,44(12):143-145,149.DING Y H,ZHANG X Q,XU J P,et al.Study on particle reinforced Cu matrix Cu-Ti2SnC-TiB2 composite[J].Hot Working Technology,2015,44(12):143-145,149.
[14]RUMELHART D E,HINTON G E,WILLIAMS R J.Learning rep resentations by back-propagating errors[J].Nature,1986,323:533-536.
[15]COLORNI A,DORIGO M,MANIEZZO V.Distributed optimization by ant colonies[A].Proceedings of ECAL91-European conference on artificial life[C].Paris:Elsevier Publishing,1991.134-142.
[16]刘楠，刘圆聪，姜伊辉，等.TiB2 颗粒和TiB 晶须混杂增强铜基复合材料导电率有限元模拟[J].稀有金属材料与工程，2022,51(2):559-565.LIU N,LIU Y C,JIANG Y H,et al.Simulation of electrical conductivity of (TiB2p+TiBw)/Cu composites[J].Rare Metal Materials and Engineering,2022,51(2):559-565.
[17]JORDAN M I,MITCHELL T M.Machine learning: Trends,perspectives,and prospects[J].Science,2015,349(6245):255-260.
[18]COHEN I,HUANG Y,CHEN J,et al.Pearson correlation coefficient[A].Noise Reduction in Speech Processing[C].Berlin:Springer,2009.1-4.
[19]DORIGO M,BIRATTARI M,STUTZLE T.Ant colony optimization[J].IEEE Computational Intelligence Magazine,2006,1(4):28-39.
[20]AGARAP A F.Deep learning using rectified linear units(ReLu)[J].arXiv:1803.08375,2018.