汽车工业作为我国的支柱产业之一,大力促进了经济发展。重型商用车载重量大,已成为交通运输领域重要的载运工具[1]。然而,随着重型商用车的保有量不断增加,我国能源短缺和环境污染问题越来越严峻。汽车轻量化作为汽车领域节能减排的重要举措之一,减轻重型商用车的整车整备质量能有效地减少燃油消耗并降低污染物的排放[2-4]。
悬架是汽车底盘关键部件,其性能好坏对乘员的舒适性和货物的安全性具有重要影响。平衡悬架是多轴重型商用车后悬架采用的结构形式,而平衡轴支架作为重型商用车平衡悬架的关键零件,也是平衡悬架总成中质量占比最大的零件[5-6]。现有的平衡轴支架产品质量大、结构特征复杂冗余,与同类型领先的重型商用车的平衡轴支架产品相比轻量化程度较低,制造工艺性差。随着重型商用车节能减排要求的不断提高,通过对平衡轴支架进行结构拓扑优化及轻量化设计并改善其制造工艺性具有重大意义。基于变密度法的结构拓扑优化技术是一种先进设计方法,其能够在定义的设计区域内寻找最佳传力路径并保留传力路径上的材料,目的是能够使用最少的材料、最优的工艺来实现结构最优的性能。王成波等[7]采用变密度法结构拓扑优化技术对铁路货车铸造金属模具芯盒框进行拓扑优化设计,在满足性能要求的前提下使芯盒框的质量减少21.8%。翟洪飞等[8]基于结构拓扑优化技术对轮毂电机壳进行轻量化设计,在模态分析及静力学分析的基础上以质量最小为优化目标对结构进行拓扑优化设计,优化后的轮毂电机壳固有频率有所提高,质量减少5.5%,结构的应力分布更加均匀。崔华钊等[9]以某重型商用车的车架为研究对象,针对车架质量大、结构复杂等问题,通过对典型工况下的车架强度进行有限元分析,在此基础上基于变密度法对车架进行拓扑优化设计,根据优化结果对车架重新建模并校核其性能,优化后车架的强度和可靠性满足要求,车架总成质量减少105 kg,轻量化效果显著。高扬等[10]针对某型高速列车齿轮箱的固有频率低,易与列车发生共振的问题,提出提高齿轮箱结构的固有频率的拓扑优化方案,结果表明优化后的齿轮箱固有频率有所提升,减少了发生共振的可能。
本文基于ANSYS Workbench 平台对某重型商用车平衡轴支架在3 种典型工况下的强度进行仿真分析,之后构建平衡轴支架拓扑优化初始模型,然后采用变密度法对平衡轴支架进行拓扑优化设计。根据得到的优化结果,对平衡轴支架进行模型重构,并对重构后的结构进行仿真校核,验证拓扑优化结果的合理性。最后基于优化后的平衡轴支架结构,采用铁型覆砂铸造工艺进行样件试制。
1 平衡轴支架强度分析
1.1 平衡轴支架有限元模型
某重型商用车平衡轴支架初始结构如图1 所示,其所用材质为QT900,该材质主要物理及力学性能参数如表1 所示。
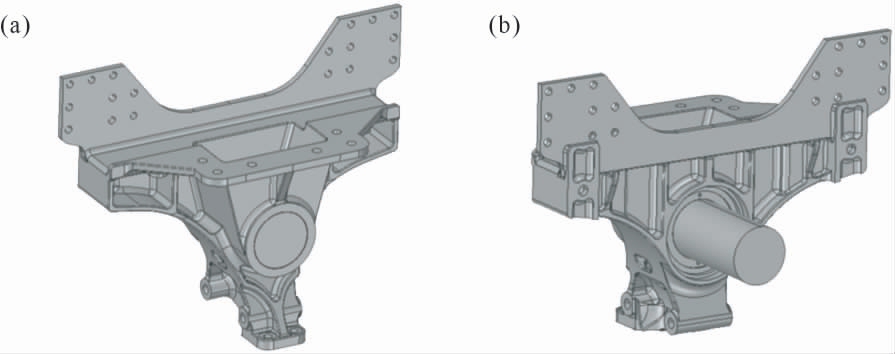
图1 某重型商用车平衡轴支架:(a)视图1,(b)视图2
Fig.1 Balance shaft bracket of a heavy commercial vehicle:(a)view 1,(b)view 2
表1 QT900材料物理性能参数
Tab.1 Physical parameters of QT900

将平衡轴支架的三维模型导入ANSYS Workbench,构建平衡轴支架的有限元模型。在建立有限元模型时,对结构进行适当的简化,删除一些对结构强度影响不大的特征。将表1 中材料属性赋给平衡轴支架,然后进行网格划分。由于平衡轴支架结构的不规则性,采用网格自动划分方法,此时网格划分可以在四面体网格划分方法和扫掠法之间切换,在模型的不同结构处采用相应的网格划分方法。这样得到的网格质量较好,避免产生畸形网格。设置全局网格尺寸为5 mm,网格划分完成后,检查该平衡轴支架有限元模型共产生2293743 个节点,网格单元数量为1583354,网格质量满足要求。平衡轴支架网格模型如图2 所示。

图2 平衡轴支架网格模型
Fig.2 Grid model of the balance shaft bracket
1.2 约束及边界条件
为了使仿真分析更加接近平衡轴支架的真实工况,需要施加合理的约束和边界条件。对有限元模型不能过度约束,过度约束会增大结构的刚性,从而会产生附加的约束力,使得有限元分析的结果不准确;有限元模型也不能欠约束,否则在求解过程中会产生刚体位移,导致结果不准确甚至求解失败。依照平衡轴支架在整车中的安装与连接关系,约束与车架相连的24 个螺栓安装孔的x、y、z 方向的平动自由度,释放其绕x、y、z 方向的旋转自由度。
1.3 载荷施加
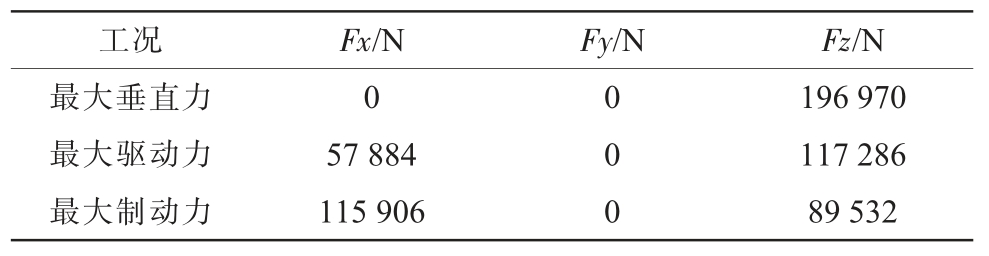
平衡轴支架在车辆运行过程中受力状态复杂,将平衡轴支架带入平衡悬架系统中进行受力分析,其受力更加接近实际工况[11]。主要分析平衡轴支架在3 种典型工况下的强度,即最大垂直力工况、最大驱动力工况、最大制动力工况。以上3 个工况是重型商用车行驶过程中较有代表性的工况,同时也是较恶劣的工况。经过分析计算得到平衡轴支架在3 种典型工况下的受力情况如表2 所示,其中Fx 为下推力杆2 个安装孔的合力,Fz 为钢板弹簧施加在平衡轴上的垂向力。
表2 平衡轴支架工况及载荷
Tab.2 Serving condition and load of the balance shaft bracket
1.4 静强度分析
根据平衡轴支架在重型商用车实际运行工况下的受力和约束,最大垂直力工况下的约束和载荷条件如图3a 所示。该工况下平衡轴受垂直方向大小为196 970 N 的力,此时下推力杆安装处不受力。采用ANSYS Workbench 结构静力学模块进行求解,得到该工况下平衡轴支架的有限元分析结果如图3b~c所示。该工况下平衡轴支架总体变形量的最大值为0.86 mm,出现在平衡轴端部位置;最大应力值为441.6 MPa,出现在平衡轴支架与平衡轴连接位置。

图3 最大垂直力工况下约束与载荷条件及静力学仿真结果:(a)约束和载荷条件,(b)位移云图,(c)应力云图
Fig.3 Constraint and load conditions and static simulation results under maximum vertical force:(a)constraint and load conditions,(b)deformation cloud diagram,(c)stress cloud diagram
最大驱动力工况时,对平衡轴支架施加的约束和载荷条件如图4a 所示,该工况下平衡轴受垂直方向大小为117 286 N 的力,下推力杆传至平衡轴支架的合力为57 884 N,方向沿x 方向。提交求解后,得到该工况下平衡轴支架的位移云图和应力云图分别如图4b~c 所示。该工况下平衡轴支架总体变形量的最大值为0.51 mm,出现在平衡轴端部位置;最大应力值为324.5 MPa,出现在与车架相连的平衡轴支架螺栓安装孔位置。
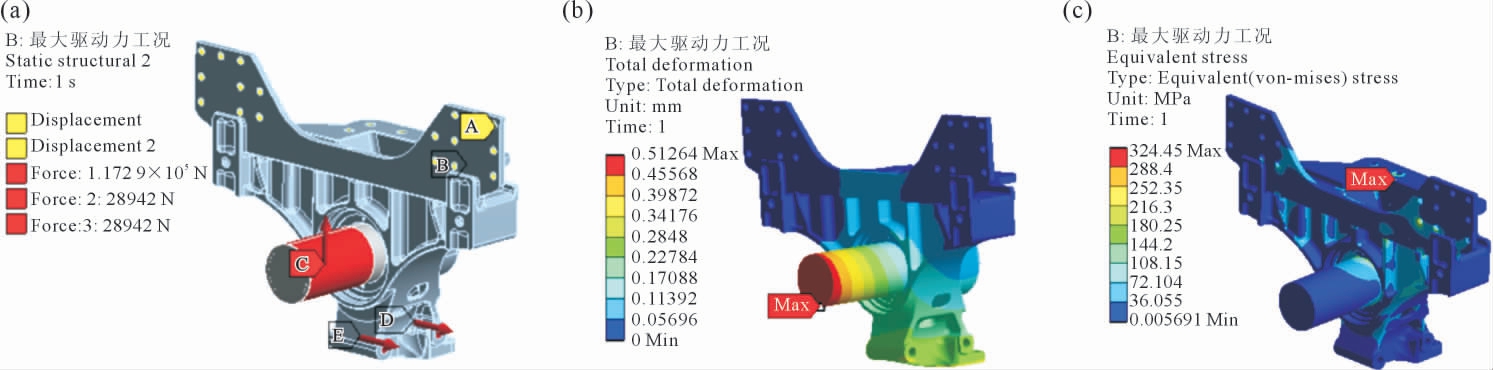
图4 最大驱动力工况下约束与载荷条件及静力学仿真结果:(a)约束和载荷条件,(b)位移云图,(c)应力云图
Fig.4 Constraint and load conditions and static simulation results under maximum driving force:(a)constraint and load conditions,(b)deformation cloud diagram,(c)stress cloud diagram
最大制动力工况下对平衡轴支架施加的约束和载荷条件如图5a 所示,该工况下平衡轴受垂直方向大小为89 532 N 的力,下推力杆传至平衡轴支架的合力为115 906 N,方向沿x 负方向。提交求解后,得到该工况下平衡轴支架的位移云图和应力云图分别如图5b~c 所示。该工况下平衡轴支架总体变形量的最大值为0.40 mm,出现在平衡轴端部位置;最大应力值为317.0 MPa,出现在与车架相连的平衡轴支架螺栓安装孔位置。
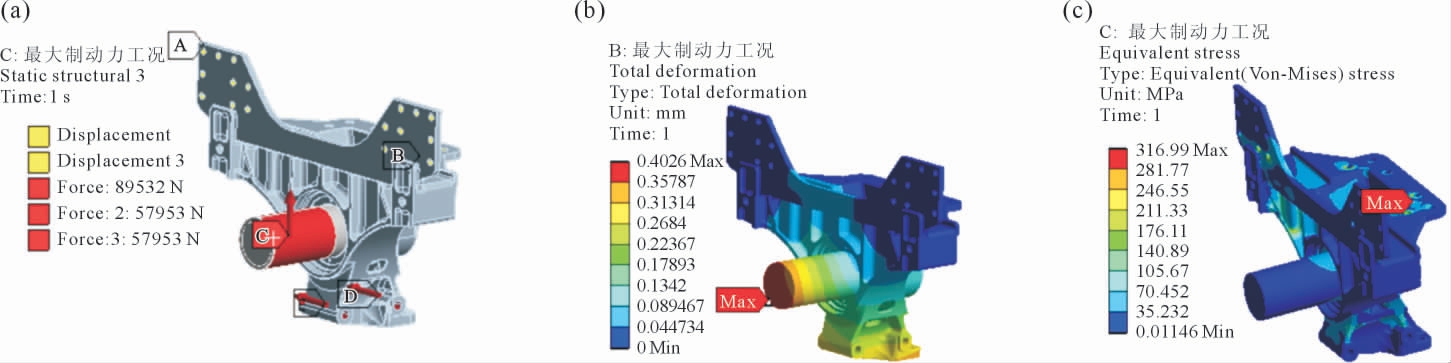
图5 最大制动力工况下约束与载荷条件及静力学仿真结果:(a)约束和载荷条件,(b)位移云图,(c)应力云图
Fig.5 Constraint and load conditions and static simulation results under maximum braking force:(a)constraint and load conditions,(b)deformation cloud diagram,(c)stress cloud diagram
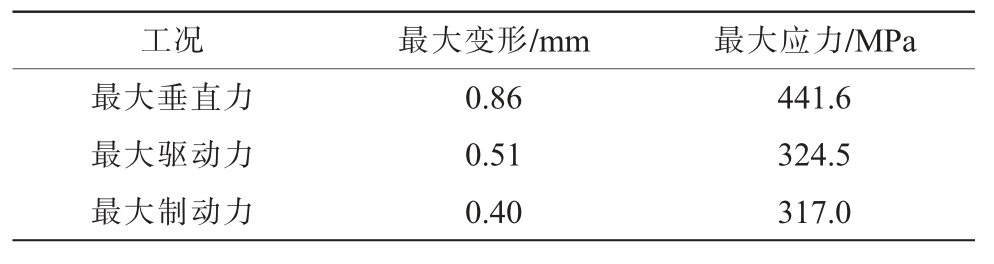
通过上述结构静力学仿真分析,得到平衡轴支架在3 种典型工况下的最大应力及变形结果如表3所示。该平衡轴支架最大应力及变形出现在最大垂直力工况,最大应力为441.6 MPa,虽小于材料的屈服极限600 MPa,但安全系数较小。另外两种工况下平衡轴支架的最大应力及变形值均较小,安全系数较大。鉴于该平衡轴支架整体较重,且应力分布极不均匀,有必要对其开展结构拓扑优化与减重设计。
表3 平衡轴支架初始结构静强度分析结果
Tab.3 Static strength analysis results of the initial structure of the balance shaft bracket
2 平衡轴支架拓扑优化设计
2.1 拓扑优化数学模型
拓扑优化技术能在设置的设计区域内根据受力情况寻找最优的材料分布,其本质就是对结构的“最大刚度”设计[12-15]。在进行结构拓扑优化过程中,设计人员只需将结构划分为优化区域和非优化区域,然后对结构施加相应的约束条件和载荷,采用数学优化算法就能实现指定区域的材料最佳分布,保留主要传力路径下的材料,而那些非主要承载区域的材料就可以去除,在满足使用要求的前提下使得材料的利用率达到最佳[16-17]。
本文采用基于变密度法的拓扑优化方法对平衡轴支架进行拓扑优化设计,以单元密度作为设计变量,结构加权应变能最小为目标,即结构的刚度最大为优化目标,结构的体积分数等为约束对平衡轴支架进行拓扑优化设计,拓扑优化的数学模型为:
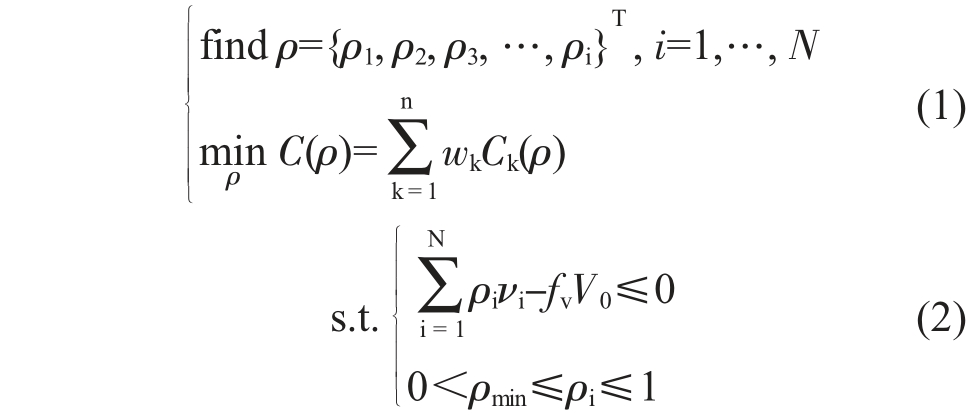
式中,ρ 为单元密度,作为设计变量;N 为单元总数;C(ρ)为结构加权柔度,最小化加权柔度作为优化目标;wk 为第k 个工况的权重因子;Ck 为第k 个工况的柔度;n 为工况数量,本文n 为3;νi 为第i 个单元的体积;fv 为体积约束对应的体积分数,取15%。另外在拓扑优化时考虑结构的制造工艺性,引入制造约束,指定脱模方向。
2.2 平衡轴支架拓扑优化有限元模型
如果在原平衡轴支架结构的基础上对其进行拓扑优化设计,那么优化后的平衡轴支架结构将受到原平衡轴支架结构的束缚,为了使得设计出的平衡轴支架结构材料分布更加合理,在平衡轴支架与车架、下推力杆等安装位置不变的情况下,将原平衡轴支架内部填实,并对外轮廓进行简化,最终构建的平衡轴支架拓扑优化初始结构如图6 所示。
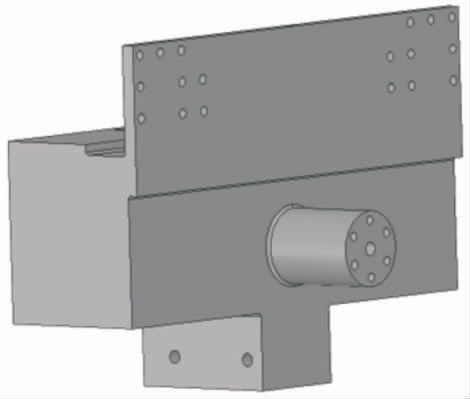
图6 平衡轴支架拓扑优化初始模型
Fig.6 Initial model of the balance shaft bracket for topology optimization
将以上构建的拓扑优化初始模型导入ANSYS Workbench 中,然后对模型划分网格,并赋予结构材料属性,施加约束和载荷条件,在3 个典型工况的基础上建立平衡轴支架多工况拓扑优化分析流程。在拓扑优化之前,需要定义模型的拓扑优化区域和非优化区域。为了保证平衡轴支架在结构优化后仍能与原来的车型进行正确安装,初始结构中安装孔的数量、位置、大小是不允许改变的;平衡轴上需要安装平衡轴毂,所以也是非优化区域。对应图7 中平衡轴支架红色区域Exclusion Region 表示非优化区域,而蓝色部分Design Region 则表示优化区域。
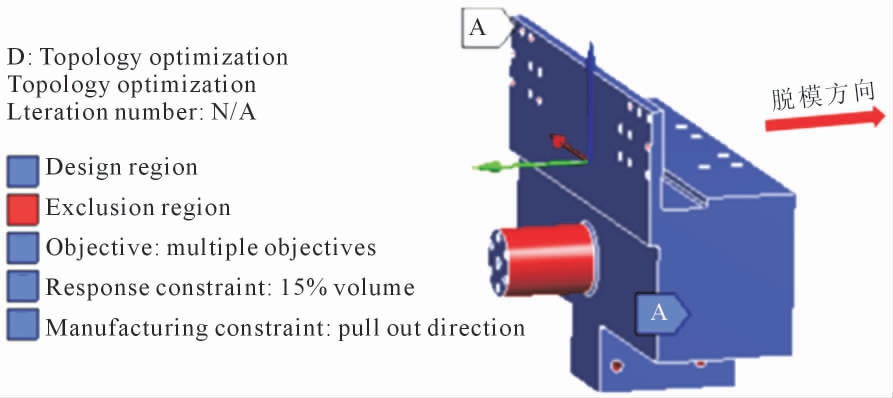
图7 优化区域和非优化区域
Fig.7 Optimized and non-optimized areas
以单元密度作为拓扑优化的设计变量,以体积减少百分比为约束函数,设置优化后的体积占平衡轴支架初始结构模型体积的15%以上,结构的加权柔度最小为目标函数,即结构刚度最大。此外,拓扑优化时需要考虑结构的制造工艺性,所以需要设置制造约束[18-19],根据现有的同类产品实际生产过程中的脱模方向,在拓扑优化设置时指定脱模方向如图7 所示。
2.3 拓扑优化结果
采用ANSYS Workbench 结构拓扑优化模块进行求解,经过共35 次迭代后收敛,得到拓扑优化结果如图8a 所示。拓扑优化密度分为3 个范围,其中红色部分的单元密度值在0~0.4 之间,表示此部分的材料可以完全去除;而单元密度值在0.4~0.6 范围内时,表示此部分的材料处于可以去除和保留之间;单元密度值在0.6~1.0 之间的部分则需要保留,越接近1 表示这部分单元越重要。阈值为0.6 的拓扑优化结果如图8b 所示。
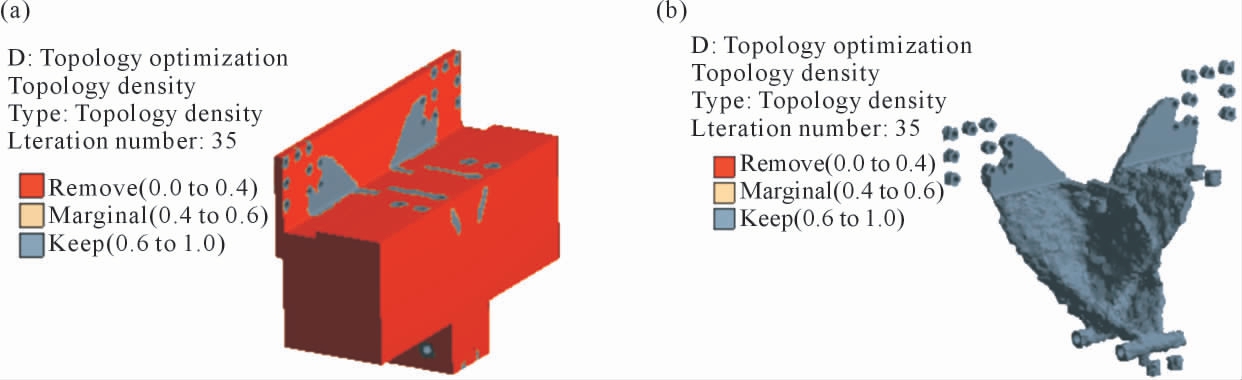
图8 结构拓扑优化结果:(a)第35 次迭代优化结果,(b)阈值为0.6 时的优化结果
Fig.8 Structure topology optimization result:(a)optimization results of the 35th iteration,(b)optimization results at a threshold of 0.6
2.4 基于拓扑优化结果的平衡轴支架模型重构
根据拓扑优化结果并考虑制造工艺性,构建优化后的平衡轴支架三维模型。图9 所示为优化后的平衡轴支架模型,优化后的平衡轴支架重54.8 kg,相比优化前重量减少了47.7 kg,减重达到46.5%。
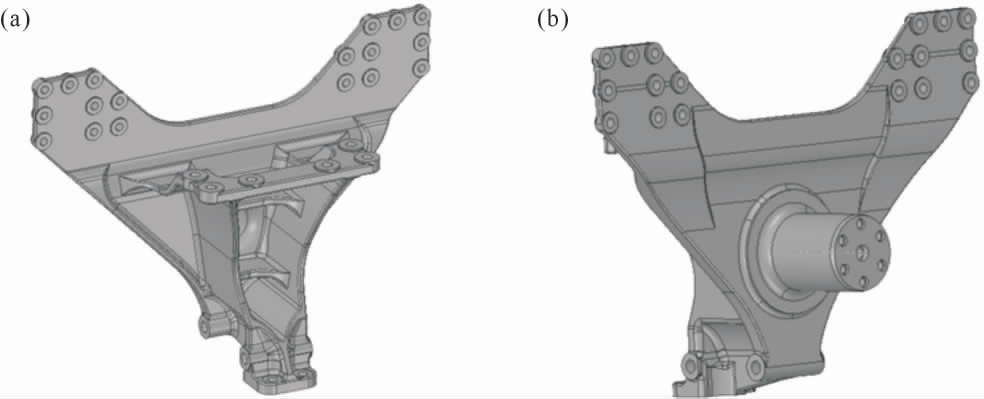
图9 结构拓扑优化后的平衡轴支架:(a)视图1,(b)视图2
Fig.9 Balance shaft bracket after structure topology optimization:(a)view 1,(b)view 2
3 优化后的平衡轴支架强度校核
为了校核拓扑优化后的平衡轴支架结构强度,对优化后的模型施加的载荷和边界条件与第二部分时相同,即对优化后的模型在最大垂直力、最大驱动力、最大制动力3 种工况下进行静力学仿真分析。如图10 所示为最大垂直力工况下优化后的平衡轴支架静力学仿真结果,可以看出该工况下平衡轴支架总体变形量的最大值为0.99 mm,出现在平衡轴端部位置;最大应力值为357.4 MPa,出现在与车架相连的平衡轴支架螺栓安装孔位置。
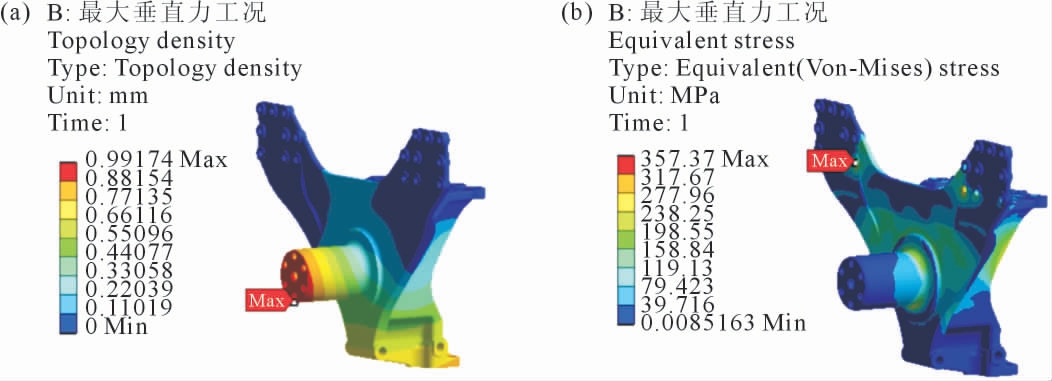
图10 优化后的平衡轴支架在最大垂直力工况下的静力学仿真结果:(a)位移云图,(b)应力云图
Fig.10 Static structure simulation results of the optimized balance shaft bracket under maximum vertical force:(a)deformation cloud diagram,(b)stress cloud diagram
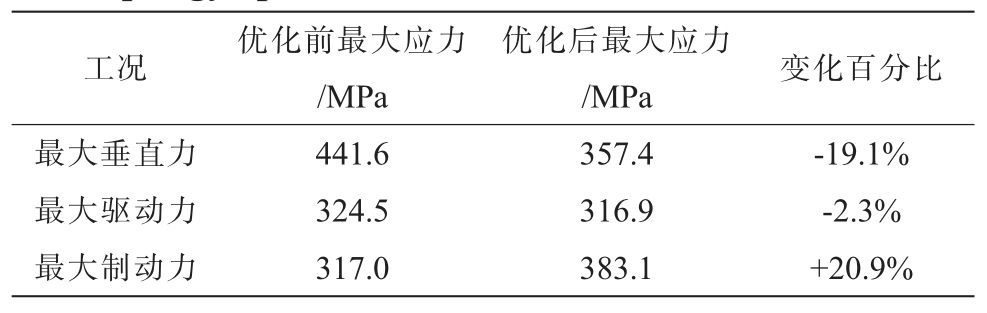
同样进行最大驱动力工况及最大制动力工况下优化后的平衡轴支架静力学仿真,表4 汇总并对比分析了平衡轴支架拓扑优化与轻量化设计前后的应力分布情况。最大垂直力工况下优化后的平衡轴支架的最大应力比优化前减小19.1%,最大驱动力工况下优化后的平衡轴支架的最大应力比优化前减少2.3%,而在最大制动力工况下,优化后的平衡轴支架最大应力值与优化前相比有所上升,但仍远小于材料的屈服极限。综上所述,拓扑优化与轻量化设计后的平衡轴支架在3 种典型恶劣工况下的应力分布更加均匀,结构的安全性能得到了显著提升。
表4 平衡轴支架拓扑优化前后的最大应力对比
Tab.4 Maximum stress comparison before and after topology optimization of the balance shaft bracket
4 平衡轴支架的试制
根据优化后的平衡轴支架结构,采用铁型覆砂铸造工艺进行样件试制[20],设计浇注系统如图11 所示。铸件材质为QT900,采用侧注式浇注,一箱浇注两件,其中直浇道浇注半径为30 mm,浇注温度为1 410~1 420 ℃,浇注速度0.3 m/s。试制的平衡轴支架铸件实物如图12 所示,经过铸件尺寸、外观及内部质量检测,铸件表面无粘砂和裂纹,铸件内部无明显缩松缩孔等铸造缺陷。试制样件外形尺寸与内部质量均满足要求,验证了优化后的平衡轴支架结构具有良好的制造工艺性。
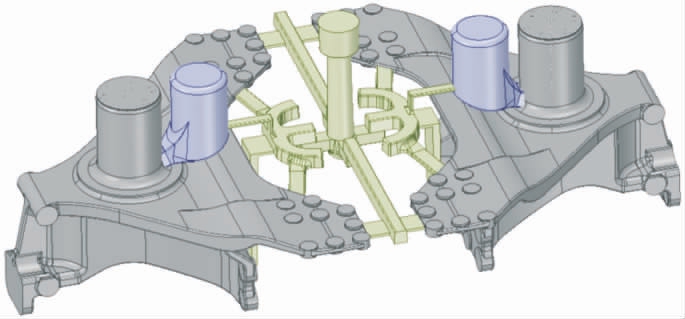
图11 平衡轴支架浇注系统
Fig.11 Gating system of the balance shaft bracket

图12 平衡轴支架实物图:(a)视图1,(b)视图2
Fig.12 Sample of balance shaft bracket casting:(a)view 1,(b)view 2
5 结论
(1)通过对某重型商用车平衡轴支架在3 种典型工况下的静强度分析,得到平衡轴支架的最大等效应力和最大位移,均满足使用要求,从分析结果得出该平衡轴支架结构应力分布极不均匀,结构冗余,有轻量化设计空间。
(2)采 用ANSYS Workbench 的Topology Optimization 模块对平衡轴支架进行拓扑优化设计,参考拓扑优化结果并根据平衡轴支架的装配要求及考虑制造工艺性,对平衡轴支架模型进行重构,优化后的平衡轴支架重量减少47.7 kg,实现减重46.5%,同时优化后的平衡轴支架在最大垂直力工况及最大驱动力工况下的最大应力比优化前分别减少19.1%和2.3%,最大制动力工况下的最大应力虽有所提高,但仍远小于材料的屈服极限;在满足平衡轴支架刚强度要求的前提下实现了轻量化设计。
(3)根据优化后的平衡轴支架结构,设计相应的浇注系统对平衡轴支架进行样件试制,试制样件的外形尺寸及内部质量均满足要求,优化后的平衡轴支架结构具有良好的制造工艺性。
[1] 王超.重型商用汽车轻量化研究[D].西安:长安大学,2019.WANG C,Heavy commercial vehicle lightweight research[D].Xi'an:Chang'an University,2019.
[2] 张楠.浅谈中国商用汽车节能与轻量化的意义与愿景[J].汽车文摘,2020,537(10):7-15.ZHANG N.The significance and vision of energy saving and lightweight commercial vehicles in china[J].Automotive Digest,2020,537(10):7-15.
[3] 任佳智,徐帆.浅谈汽车轻量化技术[J].内燃机与配件,2021,340(16):177-178.REN J Z,XU F.Talking about lightweight technology of automobile[J].Internal Combustion Engine &Parts,2021,340(16):177-178.
[4] 周伟,苏世荣,储胜林,等.汽车轻量化研究[J].汽车工程师,2019,261(1):21-24.ZHOU W,SU S R,CHU S L,et al.Research on automobile lightweight[J].Auto Engineer,2019,261(1):21-24.
[5] 李雨宣.某重型汽车平衡悬架轻量化设计[D].重庆:重庆理工大学,2019.LI Y X,Lightweight design of balance suspension for a heavy vehicle[D].Chongqing:Chongqing University of Technology,2019.
[6] 王焕美.基于某重型车的平衡悬架结构优化设计[D].长沙:湖南大学,2012.WANG H M.Optimal design of balanced suspension structure based on a heavy vehicle[D].Changsha:Hunan University,2012.
[7] 王成波,李林杰,王广欣,等.铁路货车铸件用模具芯盒框结构优化设计[J].铸造技术,2015,36(4):1069-1071.WANG C B,LI L J,WANG G X,et al.Optimization design of box core frame structure for railway wagons castings[J].Foundry Technology,2015,36(4):1069-1071.
[8] 翟洪飞,侯俊剑,房占鹏,等.基于拓扑优化的轮毂电机壳体结构轻量化研究[J].机械设计,2022,39(1):105-110.ZHAI H F,HOU J J,FANG Z P,et al.Research on lightweight design of the hub motor's shell structure based on topology optimization[J].Journal of Machine Design,2022,39(1):105-110.
[9] 崔华钊,康淑秀,马昊堃,等.基于变密度法的重型商用车车架拓扑优化设计[J].重型汽车,2022,188(2):16-18.CUI H Z,KANG S X,MA H K,et al.Topology optimization design of heavy commercial vehicle frame based on variable density method[J].Heavy Truck,2022,188(2):16-18.
[10] 高扬,阙红波,卞翔,等.高速动车组齿轮箱箱体拓扑优化设计[J].机械强度,2022,44(4):978-983.GAO Y,QUE H B,BIAN X,et al.Topology optimization design of high speed emu gearbox[J].Journal of Mechanical Strength,2022,44(4):978-983.
[11] 王霄锋.汽车悬架和转向系统设计[M].北京:清华大学出版社,2015.WANG X F.Design of automobile suspension and steering system[M].Beijing:Tsinghua University Press,2015.
[12] 付稣昇.ANSYS Workbench 17.0 数值模拟与实例精解[M].北京:人民邮电出版社,2017.FU S S.ANSYS Workbench 17.0 numerical simulation and real column refinement[M].Beijing:The People's Posts and Telecommunications Press,2017.
[13] 杜庚艺,张忠明,雷宇,等.减速机箱体的结构优化设计与铸造工艺优化模拟[J].铸造技术,2019,40(10):1071-1075.DU G Y,ZHANG Z M,LEI Y,et al.Structure optimization design and casting process optimization of reducer box[J].Foundry Technology,2019,40(10):1071-1075.
[14] 徐鑫海,韩振南.基于Hypermesh 的牵引车车架拓扑优化及有限元分析[J].汽车技术,2013,456(9):6-9.XU X H,HAN Z N.Topological optimization and finite element analysis of tractor frame based on hypermesh[J].Automobile Technology,2013,456(9):6-9.
[15] 张翼,谢俊,张钦修,等.某型号内燃机活塞结构拓扑优化及实验验证[J].铸造技术,2018,39(12):2646-2650,2655.ZHANG Y,XIE J,ZHANG Q X,et al.Structural topology optimization and experimental verification to design of piston for engine[J].Foundry Technology,2018,39(12):2645-2650,2655.
[16] 步伟顺,杨云,唐苑寿,等.基于ANSYS Workbench 的制动器支座拓扑优化[J].现代制造技术与装备,2019,275(10):38-40,43.BU W S,YANG Y,TANG Y S.Topological optimization of the brake of support based on ANSYS Workbench[J].Modern Manufacturing Technology and Equipment,2019,275(10):38-40,43.
[17] 李学忠.某重型商用车平衡轴支架轻量化设计与研究[D].太原:中北大学,2014.LI X Z.Lightweight design and research for balance-axle brackets of heavy-duty commercial truck[D].Taiyuan:North University of China,2014.
[18] 张建振,吴晓涛,刘兆英,等.基于铸造缺陷和结构强度CAE 的平衡悬架支架轻量化设计[J].汽车技术,2014,464(5):9-12.ZHANG J Z,WU X T,LIU Z Y,et al.Lightweight design of balancing suspension bracket based on casting defects and structure strength CAE[J].Automobile Technology,2014,464(5):9-12.
[19] 时培成,周永,高立新.基于制造工艺约束的悬架控制臂拓扑优化[J].机械设计,2013,30(10):39-45.SHI P C,ZHOU Y,GAO L X.Topology optimization for control arm of vehicle suspension with manufacturing constraints[J].Journal of Machine Design,2013,30(10):39-45.
[20] 夏小江,潘东杰,应浩.铸钢件的铁型覆砂铸造工艺与实践[J].铸造技术,2020,41(11):1070-1073.XIA X J,PAN D J,YING H.Process and practice of sand-lined metal molding technology for steel casting[J].Foundry Technology,2020,41(11):1070-1073.