数字化冷冻砂型绿色铸造技术采用水作为黏结剂,干砂与水充分混合后在低温环境下冻结成砂坯, 砂坯在制备过程中避免了树脂黏结剂的使用,从根本上解决了树脂砂型在制备和浇注过程中产生废气和废砂而带来的环境污染问题。 冷冻砂型数字化铣削成形技术是将具备一定强度的冷冻砂坯在数字化无模铸造精密成形机上直接进行铣削加工获得砂型单元的砂型制备方法[1]。
冷冻砂型是型砂颗粒在黏结剂的黏结作用下组成的离散颗粒体,不同于连续介质的铣削成形,砂型铣削力的大小取决于黏结剂的黏结强度,砂型切削力随着型砂抗拉强度增加而增加[2]。 铣削力越大,作用在刀具和砂型上的摩擦力越大,摩擦产热越多[3],局部温升会导致受冰晶黏接作用的砂粒脱离砂型基体而造成非加工误差。 另外,铣削力增大也会导致薄壁砂型结构破裂或坍塌,型腔表面出现裂纹或结构不完整等缺陷,降低砂型抗击液体金属流动冲击的能力[4,5]。 作用在聚晶金刚石刀具上的铣削力将直接引起金刚石颗粒内部和金刚石颗粒间黏结材料(Co)的高接触应力,从而引起刀具磨损,降低砂型的加工精度及刀具使用寿命[6]。
冷冻砂型的强度来源于冰晶黏结桥的黏接强度,铣削成形参数是影响冰晶黏结桥断裂的关键因素。 通过实验分析对树脂砂型铣削力进行预测,建立铣削参数对铣削力的影响规律[7,8],但预测模型未考虑铣削力信号随时间信号的变化;通过神经网络方法对铣削力进行建模分析,实现低硬度零件铣削力的预测与控制[9-11],但尚未建立单一铣削参数对铣削力的影响机理。 因此本文选取不同的铣削参数进行冷冻砂型铣削成形,对采集的铣削力信号进行分析,建立单一铣削参数对冷冻砂型铣削力的影响机理。 由于铣削力信号的主成分及独立成分并不清楚, 未经处理的铣削力信号还会夹杂噪声影响信号,使得铣削力的精度变低甚至失去使用价值[12-14]。对铣削力信号进行快速傅里叶变换分析铣削力信号在频域内的功率分布,去除频域内功率较低的谐波频率,保留功率较高的谐波频率可降低铣削力信号的噪声干扰,获得更加准确的铣削力信号[15-18]。
1 实验材料与方法
选用直径为8 mm的圆柱立铣刀进行冷冻砂型铣削力试验,型砂材料选用70/140目普通烘干硅砂,黏结剂为纯净水,水加入量为5%(质量分数),湿砂型经过充分混合搅拌、震动压实后放置在环境温度为-25~-20 ℃的恒温箱内保存24 h。 9253B测力计、1677A5高阻抗信号电缆、5070A多通道电荷放大器、6797数据采集器和终端计算机组成铣削力测量链对铣削力进行测量计算。
圆柱立铣刀铣削加工成形的冷冻砂型为直壁型腔面,在刀具加工平面上的砂型形状由直线形和圆弧线形两种路径组成,圆弧线形可视作由进给方向沿着圆弧切线方向的直线形组成,圆弧切线方向由初始位置和时间决定,因此只需要确定单向进给时的铣削力随时间信号的变化规律即可。 铣削方向变化时可通过向指定坐标系内做铣削力的正交分解计算[19]。
将砂型完全冻结成型后放置在9253B测力仪上, 测力仪放置在SMM200数字化无模铸造精密成形机上,测量原理如图1所示。刀具沿着机床坐标x向进行单向逆铣加工, 测量铣削过程中沿刀具进给方向的铣削力。
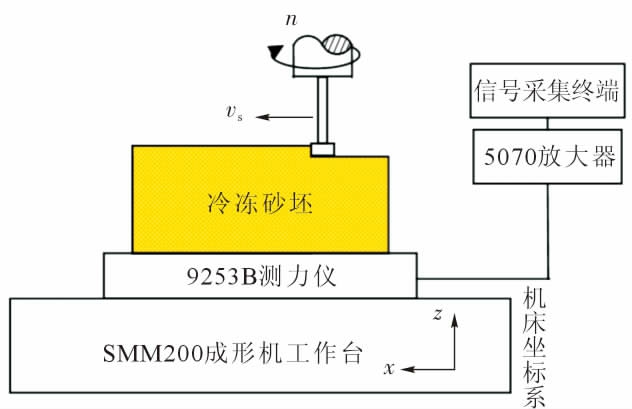
图1 铣削测试系统
Fig.1 Milling test system
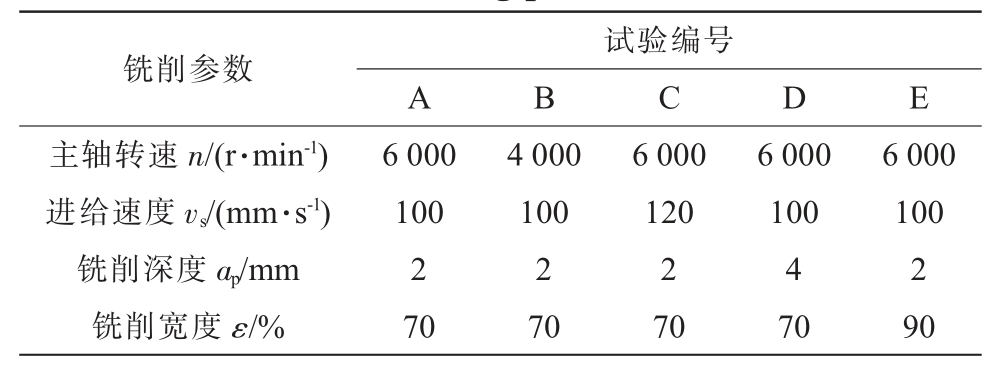
冷冻砂型铣削过程中,主轴旋转做周期运动,主轴在整数周期内的受力状态相同, 铣削力的周期与主轴转速呈负相关。在一个主轴转速周期内,随着进给速度、铣削宽度和铣削深度的增大,冷冻砂型的铣削断裂区域增大。 因此选取主轴转速、进给速度、铣削宽度和铣削深度开展铣削参数对铣削力的影响机理试验。 试验参数选取如表1所示,其中铣削宽度通过刀具直径的百分比反映其对铣削力的影响。 选用9253B切削力测量链记录铣削力随时间的变化,其中铣削力的数据采集频率选为1 000 Hz, 远大于铣削力的周期n/60[20-23],加工温度维持在-25~-20 ℃之间。
表1 铣削参数
Tab.1 Milling parameters
?
2 实验结果及讨论
将试验测得的铣削力信号进行选段处理, 选取铣削力信号稳定的一段时间内的铣削力信号进行分析处理。图2(a)为参数A条件下的铣削力信号的时域波形图,从图中可以看出铣削力信号周期性明显,幅值稳定,但信号内含有大量的噪声干扰,对铣削力的时域信号做快速傅里叶变换进行频域分析如图2(b),从铣削力信号的频域图可以看出,200 Hz处的铣削力信号功率集中, 且远高于其他频率信号的功率值,因此铣削力信号由200 Hz的信号组成,其余均视为噪声干扰, 这证明铣削力信号由单一信号组成。对冷冻砂型铣削力信号做带通滤波器设计,滤波器通带上下频率设为199 Hz和201 Hz, 滤波后时域信号周期为0.005 s,铣削力信号幅值稳定在9.0 N。
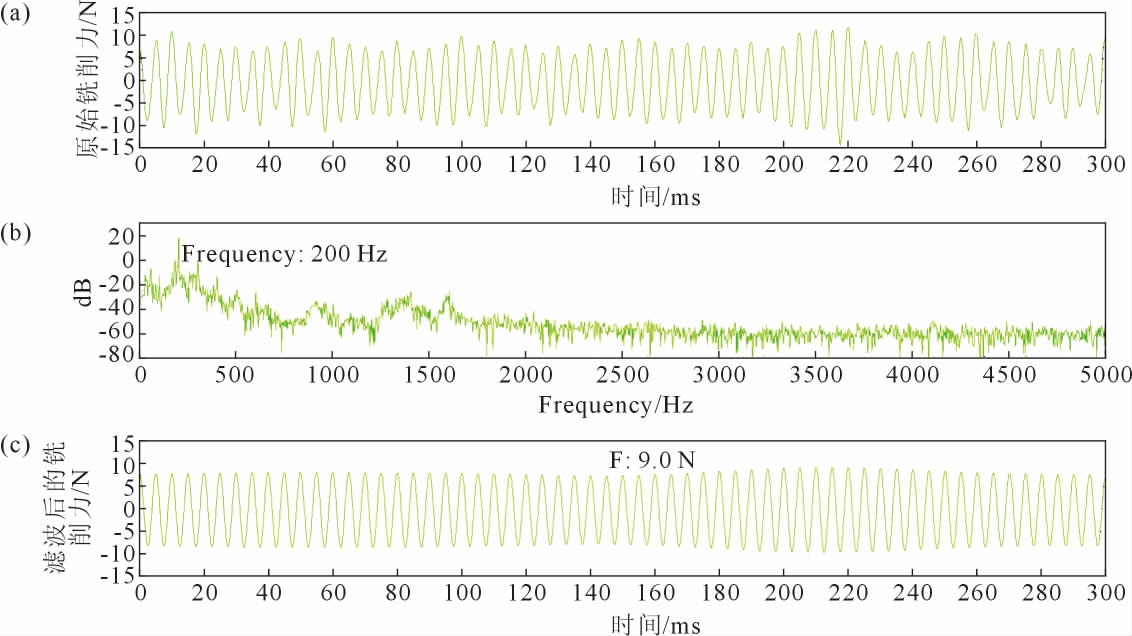
图2 参数A 铣削力信号分析:(a)原始铣削力信号,(b)频谱分析,(c)滤波后的铣削力信号
Fig.2 Milling force signal analysis of parameter A:(a)the original milling force signal,(b)spectrum analysis,(c)the filtered milling force signal
通过控制变量法探究铣削参数对冷冻砂型铣削力的影响规律。 图3为主轴转速对铣削力影响信号分析,对铣削力信号进行快速傅里叶变换,B铣削参数条件下铣削力信号能量集中在133 Hz左右,铣削周期为0.007 7 s左右, 这证明主轴转速影响铣削力信号的周期。 刀具受主轴高速旋转的传动实现周期性的进给,参数A的主轴转速周期为0.01 s,铣削力信号周期为0.005 s, 参数B的主轴转速周期为0.015 s,铣削周期为0.007 7 s左右。 由此可知铣削力信号的周期是主轴转速周期的一半, 这是因为选取的刀具有两个刀刃, 在一个旋转周期内不存在两个刀刃同时受力的状况, 因此铣削力经历两个完整循环, 对参数B的能量集中频率进行修正为133 Hz,铣削周期为0.075 s。 对铣削力信号进行带通滤波器设计,铣削力信号的幅值为9.5 N,铣削力的周期与主轴转速周期呈正比。
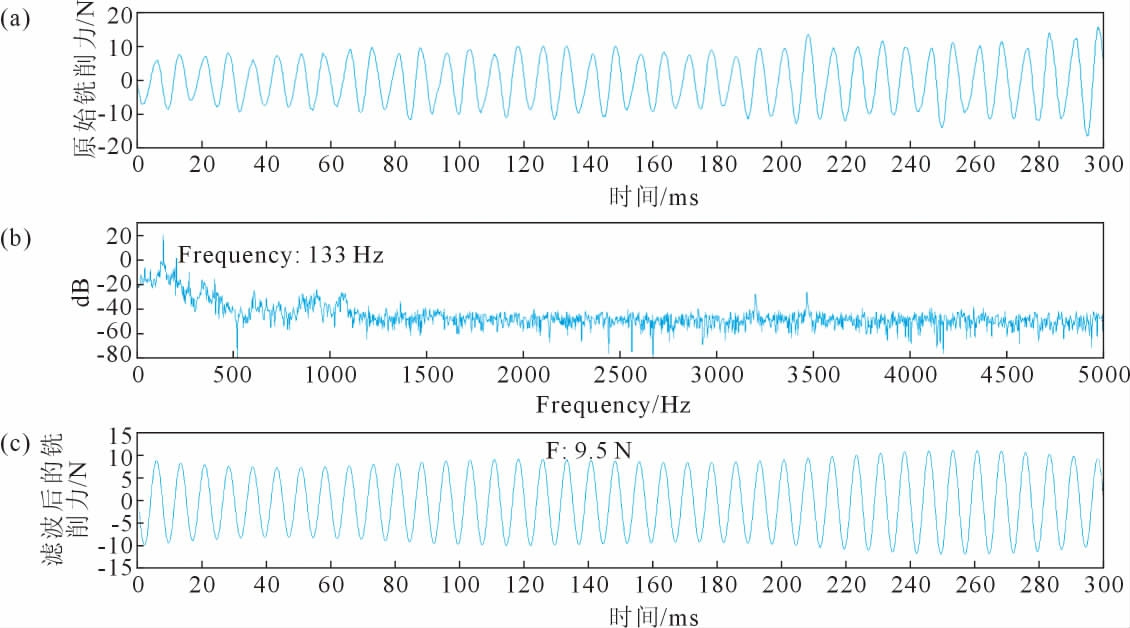
图3 参数B 铣削力信号分析:(a)原始铣削力信号,(b)频谱分析,(c)滤波后的铣削力信号
Fig.3 Milling force signal analysis of parameter B:(a)the original milling force signal,(b)spectrum analysis,(c)the filtered milling force signal
图4为进给速度对冷冻砂型铣削力影响信号分析,铣削力信号能量集中集中在200 Hz,铣削周期为0.005 s,铣削力信号的幅值为10.5 N,进给速度较对照组增大20%,铣削周期不变,铣削力增大了16.7%;图5为铣削深度对冷冻砂型铣削力影响信号分析,铣削力信号能量集中在200 Hz,铣削周期为0.005 s,铣削力信号的幅值为20.5 N, 铣削深度较对照组增大100%,铣削力增大了127.8%;图6为铣削宽度与刀具直径的比值对冷冻砂型铣削力影响信号分析,铣削力信号能量集中在200 Hz,铣削周期为0.005 s,铣削力信号的幅值为12 N, 铣削宽度与刀具直径的比值较对照组增大28.6%,铣削力增大了33.3%。 这表明进给速度、铣削宽度和铣削深度仅影响铣削力信号的幅值,铣削力随着参数取值的增大而增大,周期不受影响。
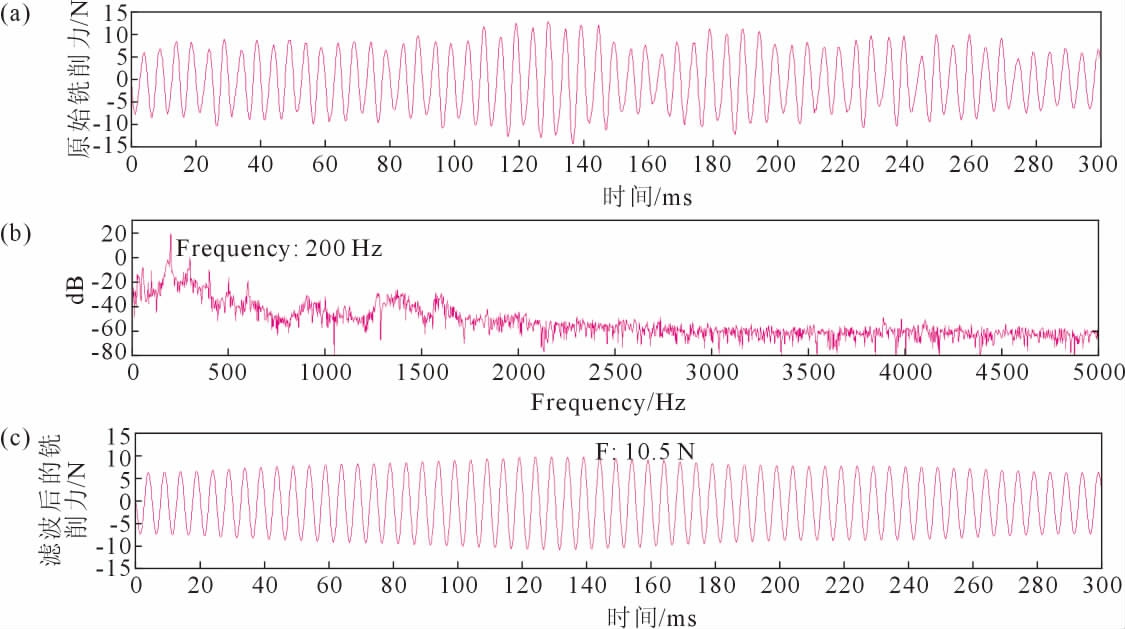
图4 参数C 铣削力信号分析:(a)原始铣削力信号,(b)频谱分析,(c)滤波后的铣削力信号
Fig.4 Milling force signal analysis of parameter C:(a)the original milling force signal,(b)spectrum analysis,(c)the filtered milling force signal
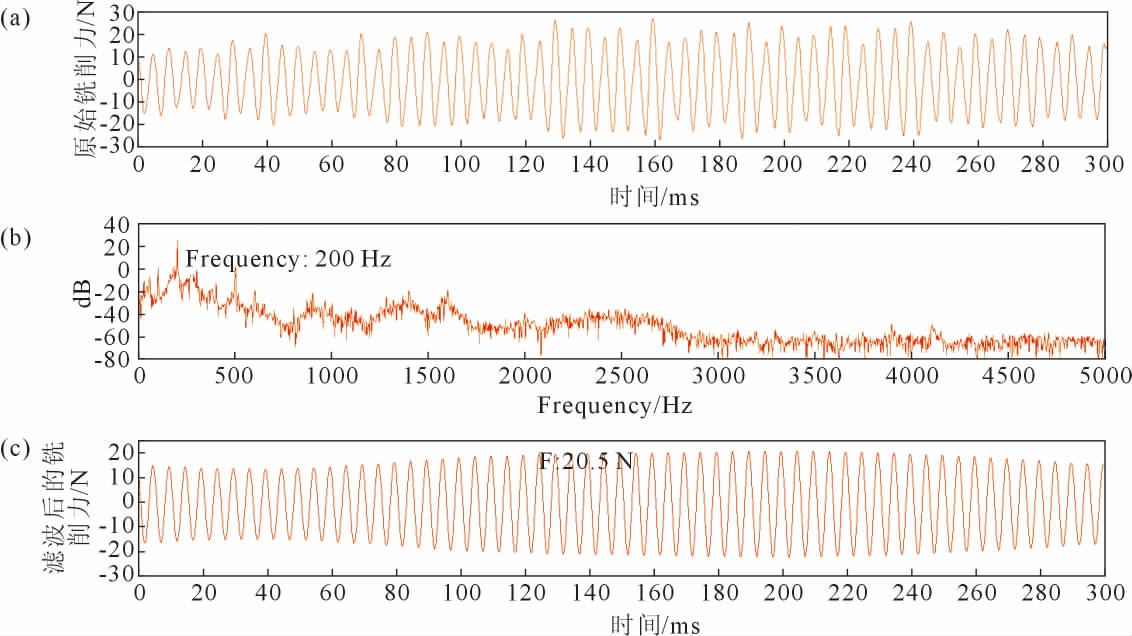
图5 参数D 铣削力信号分析:(a)原始铣削力信号,(b)频谱分析,(c)滤波后的铣削力信号
Fig.5 Milling force signal analysis of parameter D:(a)the original milling force signal,(b)spectrum analysis,(c)the filtered milling force signal
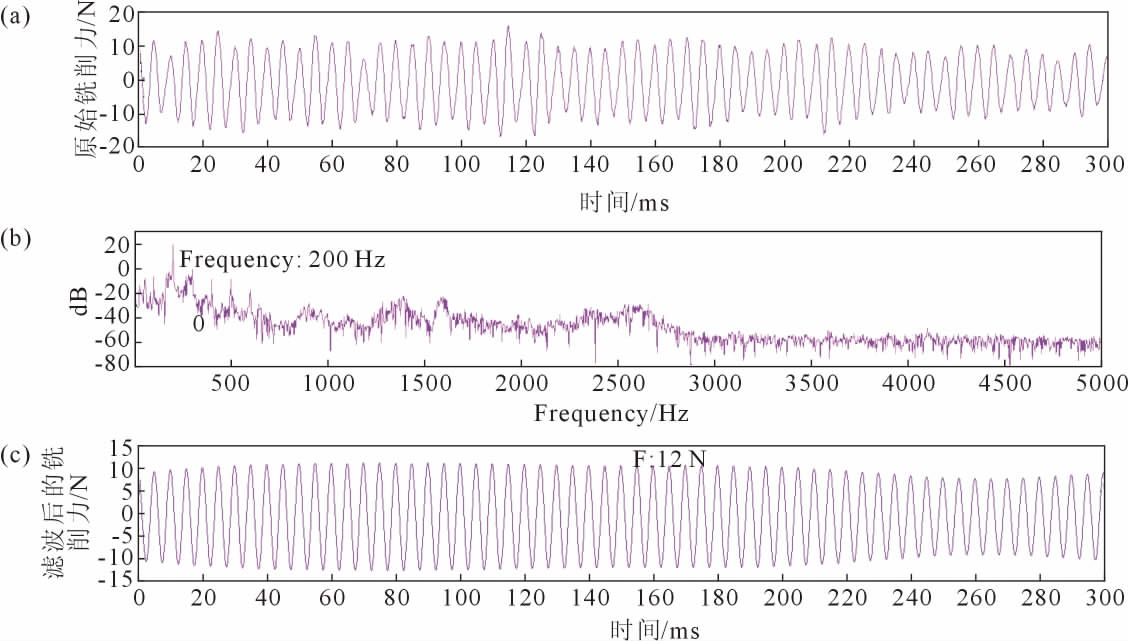
图6 参数E 铣削力信号分析:(a)原始铣削力信号,(b)频谱分析,(c)滤波后的铣削力信号
Fig.6 Milling force signal analysis of parameter E:(a)the original milling force signal,(b)spectrum analysis,(c)the filtered milling force signal
宏观尺度上,冷冻砂型可视为连续介质,砂型受到刀具的挤压作用发生断裂,被挤压的砂型区域形成废砂,在细观尺度上,砂型与高速运动的铣刀发生挤压碰撞,剪切面内的黏结桥发生变形而引起铣削层内砂型沿剪切面产生位移直至黏结桥全部断裂。 因此冷冻砂型铣削力宏观表现为铣削过程中垂直刀具前刀面的压力和沿着前刀面与型砂颗粒飞离基体的方向相反的摩擦力, 细观表现为使得冷冻砂型剪切面上黏结桥破坏, 型砂颗粒脱离冷冻砂型基体的剪切力, 即冷冻砂型剪切面断裂强度与断裂面面积的乘积,见式(1)。 将剪切力在刀具与砂型接触面进行力的分解可得到刀具与砂型相互作用的铣削力。在剪切平面内冷冻砂型受到刀刃的挤压作用,冷冻砂型剪切断裂面内的冰晶黏结桥发生破坏, 废砂沿着剪切断裂面飞出, 剪切断裂面的面积为剪切断裂面长度与铣削深度的乘积,见式(2)。 剪切断裂面的长度求解模型如图7所示,其长度可由式(3)获得,这表明铣削宽度和铣削深度通过影响冷冻砂型铣削过程中剪切断裂面面积影响铣削力大小。
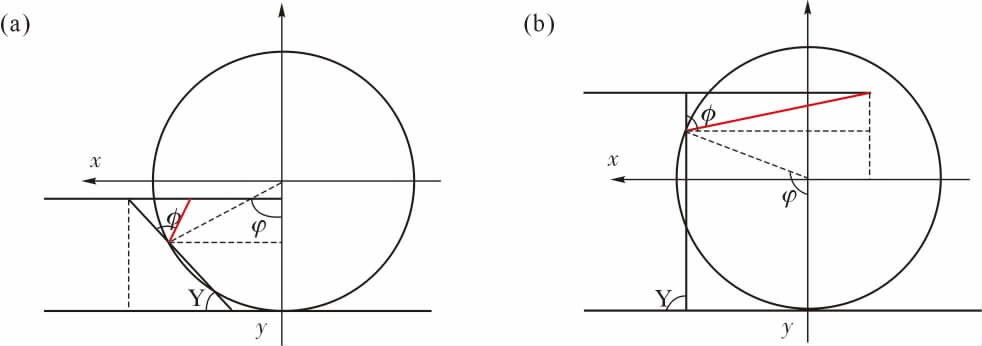
图7 剪切断裂面数学模型:(a)ae
Fig.7 Mathematical model of the shear fracture surface:(a)ae
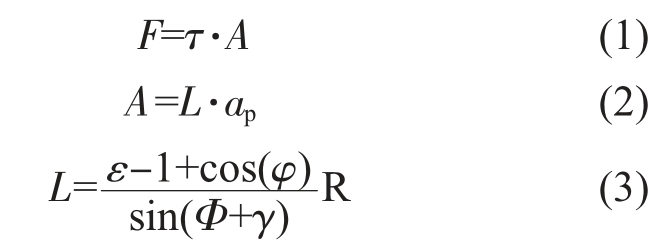
3 结论
式中,F为剪切力;τ为剪切断裂强度;L为铣削断裂长度;A为剪切断裂面积;ε为铣削宽度与刀具直径的比值;ap为铣削深度;R为刀具半径;φ为刀具转角;Φ为剪切断裂角,冷冻砂型取为30°~35°;γ为剪切断裂面的角度。
由式(2)可知,铣削深度直接影响冷冻砂型铣削断裂面积, 铣削力幅值大小与铣削深度呈正比关系,参数D的实验结果误差为13.89%;由式(3)可知铣削力随铣削宽度与刀具直径的比值增大而增大,与实验结果相符。
主轴匀速转动并匀速进给,因此在主轴完成一个旋转周期的时间内,进给速度越大,刀具前进距离越大,刀具铣削加工的冷冻砂型区域越大,破坏区域内型砂颗粒之间的黏结桥越多,所需要的能量越多,但加工时间不变,因此铣削力的幅值增大。
(1)冷冻砂型的铣削力主信号由单一信号组成,信号周期和幅值主要受主轴转速、进给速度、铣削宽度和铣削深度的影响。
(2)铣削力信号的周期与主轴转速周期成正比,铣刀有两个刀刃, 铣削力的周期为主轴转速周期的1/2。 通过控制主轴转速精确调节铣削力的周期变化, 避免刀具各刃断续的切入砂型使得刀轴受到周期作用而引发共振现象, 进而防止刀具震颤导致冷冻砂型铣削精度降低,助力铸件高质量成形。
(3)铣削力信号的幅值随着进给速度、铣削宽度和铣削深度的增大而增大, 试验结果显示进给速度增大20%,铣削力增大16.7%;铣削宽度增大100%,铣削力增大127.8%;铣削宽度增大28.6%,铣削力增大33.3%。 通过减小铣削力的幅值可以降低冷冻砂型铣削过程中刀具的磨损, 同时降低铣削过程中废砂与刀具之间摩擦力产生的热量, 进而调控冷冻砂型铣削区域的温度, 避免冷冻砂型由于局部温升而产生精度损失,提高了铸件尺寸精度。
[1] 杨浩秦.数字化无模冷冻铸造成形机理研究[D]. 北京:中国机械科学研究总院集团有限公司,2020.YANG H Q. Study on forming mechanism of digital patternless freezing casting[D].Beijing: China Academy of Machinery Science and Technology Group,2020.
[2] 刘丽敏,单忠德,兰盾,等. 基于无模铸造精密成形技术的型砂切削性能研究[J].铸造,2016,65(12):1167-1171.LIU L M,SHAN Z D,LAN D,et al.Research of cutting properties of mold sand based on the precision forming technology without pattern[J].Foundry,2016,65(12):1167-1171.
[3] 朱福先.无模砂型平头铣刀高效切削磨损机理研究[D].北京:中国机械科学研究总院集团有限公司,2018.ZHU F X. Wear mechanism research of head cutter in efficiency machining sand mould without pattern[D].Beijing:China Academy of Machinery Science and Technology Group,2018.
[4] 单忠德.无模铸造[M].北京:机械工业出版社,2017.SHAN Z D.Patternless casting[M].Beijing:China Machine Press,2017.
[5] DING H J, ZOU B, YANG J Z, et al. Instantaneous milling force prediction and valuation of end milling based on friction angle in orthogonal cutting[J].The International Journal of Advanced Manufacturing Technology,2021,116(3-4):1341-1355.
[6] 单忠德, 朱福先. 应用PCD刀具铣削砂型的刀具磨损机理和预测模型[J].机械工程学报,2018,54(17):124-132.SHAN Z D,ZHU F X.Wear mechanism and predicition model of polycrystalline diamond tool in milling sand mould [J].Journal of Mechanical Engineering,2018,54(17):124-132.
[7] 饶江华,徐志锋,谢云龙,等. 砂型铣削力的预测计算及断裂断口分析[J].铸造,2016,65(3):228-232,236.RAO J H,XU Z F,XIE Y L, et al. Sand model milling force prediction calculation and fracture surface analysis[J]. Foundry, 2016,65(3):228-232,236.
[8] 谢大进. 精密砂型数控铣削刀具切削力及磨损行为研究[D].南昌:南昌航空大学,2018.XIE D J. Study on cutting force and tool wear behavior of precision sand by NC milling[D].Nanchang:Nanchang Hangkong University,2018.
[9] LUO T,LU W,KRISHNAMURY K,et al.A neural network approach for force and contour error control in multi-dimensional end milling operations[J].International Journal of Machine Tools and Manufacture,1998,38(10-11):1343-1359.
[10] PATRA K,JHA A K,SZALAY T, et al. Artificial neural network based tool condition monitoring in micro mechanical peck drilling using thrust force signals[J].Precision Engineering,2017,48:279-291.
[11] RATCHEV S,GOVENDER E,NIKOV S,et al.Force and deflection modelling in milling of low-rigidity complex parts[J].Journal of Materials Processing Technology,2003,143-144:796-801.
[12] ZHANG K , SHI L , HU Y, et al. Variable spectral segmentation empirical wavelet transform for noisy signal processing[J].Digital Signal Processing,2021,117(6):103151.
[13] CHEN F, ZHAO H , LI D W, et al. Contact force control and vibration suppression in robotic polishing with a smart end effector[J]. Robotics and Computer-Integrated Manufacturing, 2019, 57:391-403.
[14] ZIMROZ P, TRYBAŁA P, WRÓBLEWSKI A, et al. Application of UAV in search and rescue actions in underground mine-A specific sound detection in noisy acoustic signal[J]. Energies, 2021,14(13):3725.
[15] 於玺. 快速傅里叶变换在信号处理中的应用[J]. 信息记录材料,2021,22(10):184-186.YU X. Application of fast fourier transform in signal processing[J].Information Recording Materials,2021,22(10):184-186.
[16] 林志斌,黄智全,颜林明. 一种基于交叠组合稀疏全变分的图像去噪方法[J].电子质量,2020(10):79-84.LIN Z B, HUANG Z Q, YAN L M. An image denoising method based on overlapping group sparsity total variation[J].Electronics Quality,2020(10):79-84.
[17] 王超. 基于Eisenstein基底的快速傅里叶变换算法的研究[D].合肥:中国科学技术大学,2021.WANG C. Research on fast fourier transform algorithm based on eisenstein[D].Hefei:University of Science and Technology of China,2021.
[18] WANG Y , ZHENG L, GAO Y, et al. Vibration signal extraction based on FFT and least square method[J].IEEE Access,2020,8:224092-224107.
[19] LIU S, JIN S. Predicting milling force variation in time and space domain for multi-toothed face milling[J]. The International Journal of Advanced Manufacturing Technology, 2020,108(7/8):2269-2283.
[20] 王连明,葛文奇,谢慕君. 采样频率、系统延迟对跟踪系统稳定性能的影响[J].光学精密工程,2000(4):369-372.WANG L M, GE W Q, XIE M J. Influences of sample frequency and delays on tracking system[J].Optics and Precision Engineering,2000(4):369-372.
[21] DONG J N,LI H K,FAN Z F,et al.Time-frequency sparse reconstruction of non-uniform sampling for non-stationary signal[J].IEEE Transactions on Vehicular Technology,2021,70(11):11145-11153.
[22] ESPINOSA R, TALERO J, WEINSTEIN A.Effects of tau and sampling frequency on the regularity analysis of ECG and EEG signals using ApEn and sampEn entropy estimators[J]. Entropy,2020,22(11):1298.
[23] MOSCHITTA A,COMUNIELLO A,DE ANGELIS A,et al.Effect of noise,partial synchronization,and sampling frequency inaccuracies on amplitude measurement of multiple linear chirp signals[J].Measurement,2021,181(3):109635.