金属基复合材料(metal matrix composites,MMCs)能够通过设计和改变微观结构,获得传统单相材料所不具备的优异性能,在航空航天、轨道交通和汽车工业等领域应用广泛。 特别地,具有特殊结构和纳米尺寸的石墨烯和碳纳米管(carbon nanotube,CNT)由于强度高和稳定性好,被认为是MMCs 中极具潜力的增强材料[1]。例如,CNT 作为增强体在铝中就具有优异的强化效果[2-4]。长期以来,在研究碳纳米管增强铝基(CNTs/Al)复合材料制备方法并探究其力学性能和强化机制时, 实验一直是最常用的手段[5-8]。 然而,仅通过实验研究会有大量的成本消耗,而且一些微观作用机制和复杂影响规律无法通过实验直接探明。 随着计算机软硬件技术的发展,数值模拟分析在各种复合材料研究中均得到广泛应用,很好地解决了上述难题。
通过有限元建模,能够模拟和预测复合材料在实际应用中出现的诸多现象, 如力学性能变化、增强体与基体的界面行为、弹塑性变形行为以及裂纹萌生和扩展等[9]。 复合材料在变形时,基体和增强体的各种力学响应复杂且存在交互影响。 在对复合材料进行数值模拟分析时,建立通用且完整的以及可以整合多个影响因素的数值模型仍然具有挑战性,包括预测变形和损伤过程中力学响应的本构模型以及描述复合材料组织结构特征的三维结构模型。在进行数值模拟分析时,数值模型的准确性决定着有限元分析结果的可靠性[10]。 但是,由于CNTs/Al 复合材料组织结构的特殊性和应用环境的复杂性,现有数值模型在预测变形和损伤时的适用性和准确性有待进一步提高。 近年来, 虽然国内外学者在MMCs 数值模拟研究方面取得了显著进展,然而针对CNTs/Al 复合材料变形和损伤行为的数值模拟研究还相对较少。
本文综述了目前在复合材料数值模拟分析中的几种代表性数值模型及其应用情况。 首先介绍了目前得到广泛应用的连续损伤模型和内聚力损伤模型的理论基础, 尤其关注两种模型在描述CNTs/Al复合材料变形和损伤时的基本假设和各自特点,以期对详尽建模策略和完整控制方程的确立提供思路。 随后介绍了复合材料代表性体积元(representative volume element,RVE)模型的特点及其在不同复合材料多尺度建模中的应用。
1 连续损伤模型
连续损伤模型是基于连续介质力学的唯象本构模型,对各向同性材料和各向异性材料均有较好的适用性,已被广泛用于预测材料变形时的损伤产生和演化以及相应的各向同/异性刚度退化。 同样地, 连续损伤模型能够描述CNTs 自身纳米力学响应及其与基体材料宏观力学性能之间的关系,已成为分析CNTs/Al 复合材料发生变形时增强体与基体之间的界面行为、载荷传递、变形协调等问题的有力工具。
采用连续损伤模型描述复合材料中基体开裂、增强体损伤和界面脱粘等问题有一个前提条件,即问题尺寸需大于缺陷/微裂纹尺寸[11]。 实验表明,上述假设条件在CNTs/Al 复合材料变形和损伤时能够成立,并且CNTs 的力学响应与纤维增强体类似,故采用连续损伤模型可以直观地定义CNTs/Al 复合材料中的损伤变量。
Huang 和Rodrigue[12]通过将连续介质力学与有限元相结合的方法, 对CNTs 增强聚合物基复合材料的力学性能进行了探究, 分析了不同模型对复合材料力学性能的预测结果, 获得了复合材料的弹性模量。 Wang 等[13]在连续介质力学框架下,建立了单向纤维增强复合材料静态损伤的三维非线性有限元模型, 研究了三维编织复合材料损伤与有效弹性性能之间的关系,揭示了复合材料更精确的破坏机制。Mishnaevsky 和Brøndsted[11]对比了剪力滞后模型、解析模型、纤维束模型、基于断裂力学和连续损伤力学的模型以及数值连续力学模型, 并分析了上述5 种模型在模拟纤维增强复合材料变形、 损伤和断裂时的各自优势、局限性和发展前景。 Drabek 和Böhm[14]对比了不同模型在描述非均匀材料韧性断裂时对裂纹萌生和扩展的计算能力, 重点介绍了延性损伤模型和延性损伤指标触发模型, 并采用能克服网格依赖性的非局部方法使这些模型通过用户子程序在有限元软件ABAQUS/Standard 中得以实现。
Gurson[15]通过引入孔洞体积分数f 作为损伤变量, 发展了一种修正von Mises 流动势的孔洞生长模型,主要用于模拟基于微孔形核、长大和聚合的损伤行为。在考虑孔洞之间相互作用的情况下,可给出修正的屈服函数:
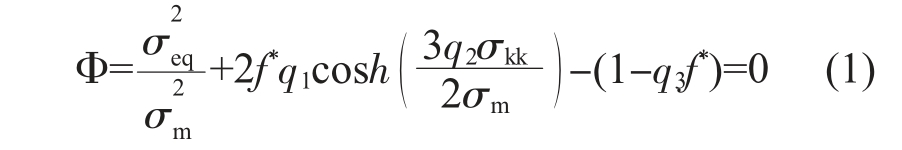
式中,σeq 为基体材料的宏观等效应力;σm 为基体材料的实际屈服应力;σkk 为基体材料的静水压力;f 为实际孔洞体积分数;f*为等效孔洞体积分数;q1、q2、q3为材料参数。 随着f 的演变,f*可表示为分段函数:
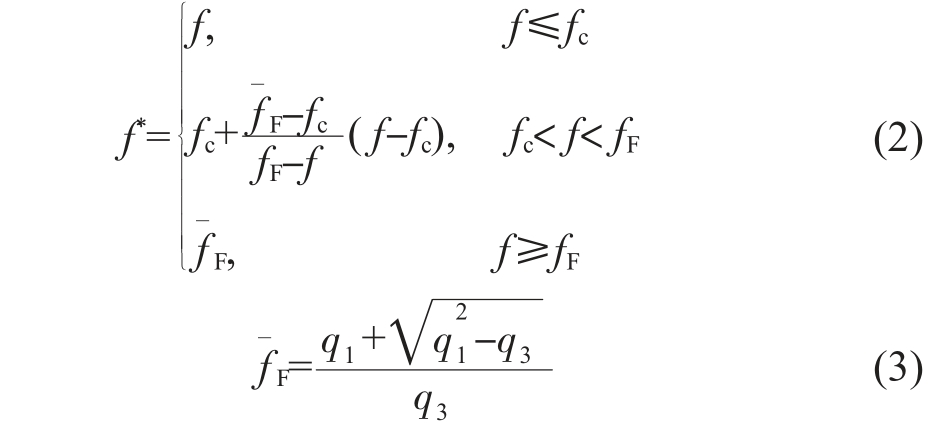
式中,fc 为临界孔洞体积分数,即孔洞开始发生聚合时的体积分数;fF 为材料断裂时的孔洞体积分数。 可以通过计算fc 和fF 确定材料的失效模式, 当fc<f<fF时,材料中的孔洞发生聚合;当f≥fF 时,材料断裂。
Rousselier[16]在上述模型的基础上提出了一种以热力学连续损伤力学方法描述延性损伤和断裂的改进方法, 能够对裂纹萌生和早期长大进行良好的预测,模型形式为:
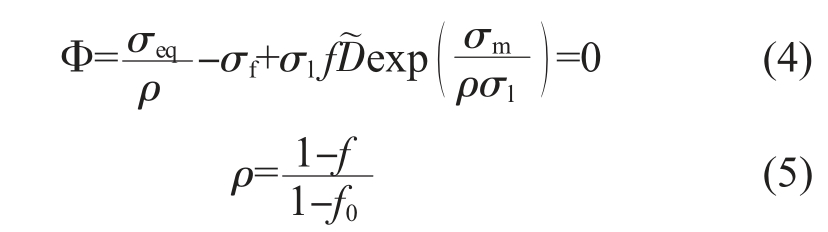
式中, f0 为延性材料的初始孔隙率;σ1 和![]() 为材料参数。
为材料参数。
此外,还可以采用基于内变量的连续介质力学方法建立纤维增强复合材料的本构模型来描述损伤增长规律,该方法需要引入相应的内部状态变量来表征损伤模式,如基体中的纤维开裂、孔隙生长或微开裂以及界面微裂纹等。 Jang 等[17]开发了适用于不同类型单向和编织复合材料的本构模型,考虑了从弹性变形到塑性变形直至最终破坏的完整变形范围内的拉压不对称性。 为了有效捕捉这种不对称性,提出了新的具有额外膨胀分量以及不同拉伸和压缩弹性模量的多变量本构模型,并且通过引入非对称破坏准则和损伤演化规律对强度进行预测。Tang 等[18]在对纤维增强MMCs 变形和应力状态相关损伤演化进行研究时,采用了修正的内变量本构模型对损伤演化和失效进行预测:
式中,φtotal 为连续体单元内材料的损伤分数;φparticles表示由颗粒脱粘和断裂引起的损伤;φpores 代表孔隙生长;C 描述孔隙的聚集和孔隙间的相互作用。 当φtotal 趋近于1 时,材料失效。
通过引入损伤变量,可以直观地描述材料的损伤和断裂。 Vignjevic 等[19]基于材料刚度张量的谱分解对应变能进行分解,并假设每个应变能分量代表一个特征变形模式的自由能,开发了能够预测纤维增强复合材料损伤行为的本构模型。 该模型基于连续损伤力学, 忽略了加载和卸载过程中迟滞的影响,将材料刚度的减小定义为损伤值d:
式中,E 为复合材料的瞬时弹性模量;E0 为复合材料的初始弹性模量。
Ismar 等[20]在对不同类型纤维增强铝基复合材料的热力学行为进行研究时,通过连续损伤力学方法将损伤融入本构方程,开发了铝基复合材料黏塑性本构模型。 该模型利用卡恰诺夫的有效应力概念引入标量损伤变量ω:
式中,σij 为应力张量的分量。
Reiner 等[21]针对ABAQUS/Explicit 和LS-DYNA 两种不同有限元软件中基于连续损伤力学的3种本构模型, 对比了它们在模拟复合材料层合板在片状和管状挤压试验中遭受轴向渐进破碎时的能力、局限性和挑战。 Vyas 和Pinho[22]在对单向纤维增强聚合物基复合材料进行本构建模时考虑了更多的特征因素,如静水压力敏感性、多轴加载效应、屈服应力对外加压力的依赖性等, 建立的本构模型包括新的屈服函数、 非关联流动法则和非线性随动强化法则, 并与适合的失效准则和相应的损伤模型相结合, 能够预测单向和多向复合材料层合板的非线性响应。 Hirsch 等[23]提出了考虑局部界面黏结失效和块体材料内聚失效的本构模型, 对铝构件和玻璃纤维增强环氧树脂的连接处进行了研究。 基体材料的行为用基于连续介质力学建立的弹塑性损伤模型来描述,采用梯度增强公式避免网格依赖,运用数值均匀化方案实现有效牵引-分离关系的预测,探明了随机粗糙界面的局部强度和几何形状对宏观性能的影响。Nguyen 和Khaleel[24]基于由损伤准则和连续介质热力学获得的损伤演化规律, 提出了一种描述随机取向短纤维复合材料基体开裂机理的微观-宏观方法, 采用消失单元技术模拟了导致宏观裂纹萌生和扩展的微观损伤积累, 该计算方法已被证明对层状复合材料结构的损伤分析是非常有效的。
2 内聚力损伤模型
内聚力损伤模型是一种基于弹塑性断裂力学的唯象模型,相关概念最初由Barenblatt 等[25]提出,后来被广泛应用于解决裂纹萌生和扩展以及复合材料界面损伤等具体的工程问题。一般认为,复合材料的界面损伤有界面层内聚破坏、 界面黏结破坏和混合破坏三种形式。其中,分层现象在纤维增强复合材料和层状复合材料的损伤失效中最为典型, 适合采用内聚力损伤模型对其描述。 在CNTs/Al 复合材料的变形和损伤数值模拟研究中, 同样可以采用内聚力损伤模型来预测CNTs 和Al 基体之间的界面损伤行为。
内聚力损伤模型的形式根据材料的张力-位移关系不同可分为双线性模型、 梯形模型和指数型模型,其中,双线性内聚力损伤模型的应用较为广泛。Guo 等[26]采用细观力学计算和宏观实验相结合的方法, 研究了单向纤维增强聚合物基复合材料在拉伸作用下的力学行为, 纤维与基体界面响应使用双线性牵引-分离定律(图1) 的零厚度内聚力单元来处理。 在无损伤情况下的非耦合牵引-分离关系为:
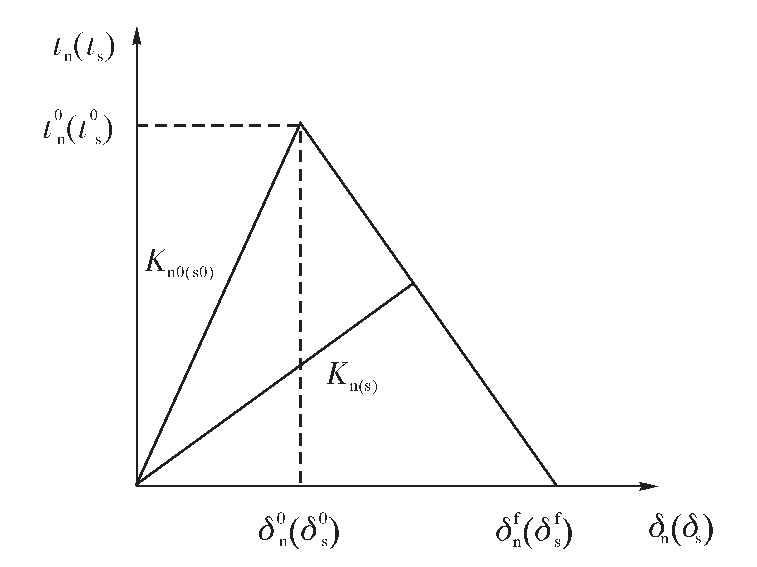
图1 内聚力单元的双线性牵引-分离规律[26]
Fig.1 Bilinear traction-separation laws for cohesive elements[26]
式中,tn 和ts 分别为某一分离位移处的法向和切向牵引力;δn 和δs 分别为法向和切向位移。 于是,定义分离位移δm 为:
在双线性牵引-分离定律下, 损伤起始点由最大牵引力控制。 当法向或切向牵引力达到最大值时,内聚力单元开始破坏:
式中![]() 分别为损伤起始点处的法向和切向牵引力。 对于损伤起始后的线性软化,损伤演化由损伤变量D 控制:
分别为损伤起始点处的法向和切向牵引力。 对于损伤起始后的线性软化,损伤演化由损伤变量D 控制:
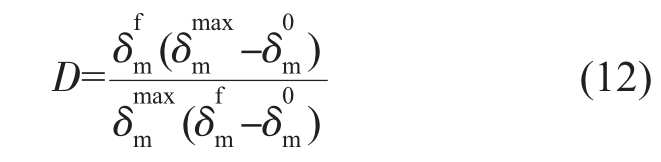
式中![]() 为有效分离位移
为有效分离位移![]() 为最大分离位移
为最大分离位移![]() 为损伤起始时的有效分离位移。 损伤演化会引起刚度退化,法向损伤刚度Kn 和切向损伤刚度Ks 分别为:
为损伤起始时的有效分离位移。 损伤演化会引起刚度退化,法向损伤刚度Kn 和切向损伤刚度Ks 分别为:
式中,Kn0 和Ks0 分别为损伤起始时法向和切向损伤刚度。 而损伤刚度的退化又影响着牵引力,牵引力的变化可以表述为:
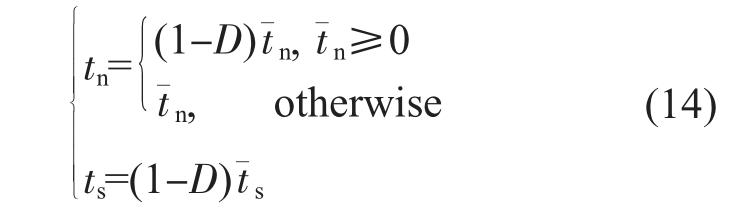
式中![]() 为损伤的法向和切向牵引力。
为损伤的法向和切向牵引力。
Hui 等[27]在对单向碳纤维增强复合材料损伤机理进行研究时,将纤维和基体之间传递复杂力学性能的结合部分认定为界面, 并采用双线性牵引-分离定律来模拟界面黏结效应的本构响应, 如图2 所示。 变形开始时, 界面的力学行为被认为是线弹性的。 随着载荷增加到界面临界强度时, 损伤开始产生,界面承载能力不断减弱直至完全消失,即发生界面脱粘。Liu 等[28]采用晶体塑性有限元法和内聚力模型相结合的方法, 从细观尺度揭示了石墨烯增强铝基复合材料在拉伸载荷下多晶铝基体、 石墨烯增强体和石墨烯-铝界面的损伤机制,研究了石墨烯形貌和初始微裂纹对复合材料破坏行为和力学性能的影响。 Shao 等[29]将位错穿孔区模型、基于Taylor 的非局部塑性理论和内聚力模型引入轴对称单元胞模型, 提出了一种改进的有限元模型来研究颗粒增强MMCs 中受颗粒尺寸影响的流动强化和界面损伤,模拟了界面脱粘对材料力学性能的影响。 Eltaher等[30]为了探明纳米复合材料弹塑性损伤行为与界面的关系, 采用单元胞代表体元和内聚单元模型探究了基体和增强体之间的结合, 证实了结合内聚单元模型的代表性体积单元能够准确模拟纳米复合材料的应力-应变行为,大大降低了三维模型的计算成本和模拟真实微观结构的二值化误差。 Kotelnikova-Weiler 等[31]研究了包含大量相互作用纤维和黏弹性基体以及纤维缺陷随机分布的复合材料在剪切-牵引联合载荷作用下的渐进损伤, 显示了基体剪切刚度与材料寿命的关系以及受额外均匀剪切应力的影响。Weng 等[32]建立三维多颗粒有限元模型探究颗粒尺寸、 形貌和界面强度对颗粒增强复合材料单轴拉伸弹塑性行为的影响, 用内聚力模型描述界面损伤,量化了微观结构特征对基体中界面损伤、载荷传递和强化效应的影响, 发现界面强度越弱界面损伤产生越早且发展越快。 Heide-Jørgensen 等[33]建立了一种解析、三维、多尺度的平纹编织混杂复合材料均匀化模型,基于详细的几何解析公式,考虑了纤维起伏、 丝束厚度和间隙以及纤维和基体材料在微观层面的脱粘。
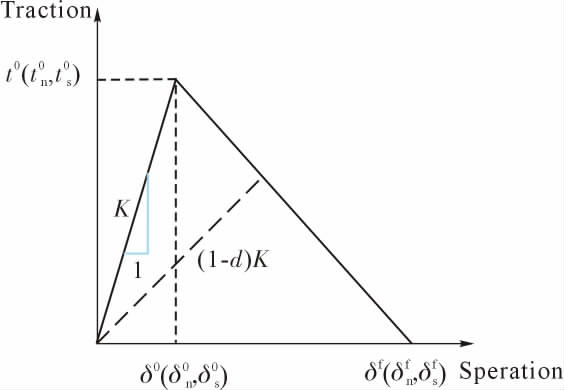
图2 界面的本构响应[27]
Fig.2 Constitutive response for the interface[27]
除了能够描述纤维或颗粒增强复合材料的脱粘,内聚力损伤模型也适用于模拟层合板的分层。Li和Chen[34]开发了预测纤维材料多裂纹破坏行为的扩展内聚力损伤模型,模拟了层状复合材料中的分层迁移,考虑了裂纹内聚效应,从破坏后能量耗散的角度引入与应变场相关的等效损伤标量来表征损伤演化。 Massarwa 等[35]为了预测复合材料层合板的力学响应,建立了基于单元细观力学的三维多尺度损伤模型,基于应变和基于应力两种破坏理论确定层板的破坏,并以用户材料子程序的形式在有限元软件中得以实现, 当损伤在宏观有限元模型内传播时, 采用单元删除法将材料点从有限元计算中剔除。 Skovsgaard 和Heide-Jørgensen[36]开发了纤维复合材料的三维均匀化模型,允许纤维和基体材料具有非线性本构关系,并在纤维和基体之间实施了牵引-分离定律,从而在微观上实现了二者的分离。 Fu和Wang[37]采用随机RVE 建立了能够对单向层合板中的内聚强度进行预测的复合材料分层微观力学模型:
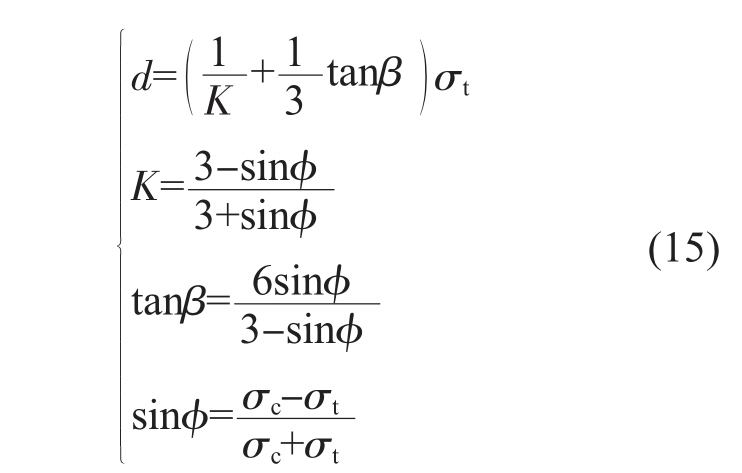
式中,d 表示材料的内聚强度;σt 和σc 分别表示拉伸和压缩的屈服应力;φ 为材料的内摩擦角;β 为应力平面内线性屈服面的斜率;K 是三轴拉伸屈服应力与三轴压缩屈服应力的比值,能够控制屈服面对中间主应力值的依赖性。 预测结果表明,内聚强度在很大程度上取决于随机微结构的类型以及由最小纤维间距和纤维排列角度描述的随机微结构形态。
3 代表性体积元及多尺度建模
上述两种模型可在适合的条件下对CNTs/Al复合材料变形和损伤行为进行预测,但在研究复合材料局部的变形机理和损伤演变规律时,还需建立能够完整呈现组织结构特征的多尺度模型,从而有助于厘清复合材料组织性能在宏观-介观-微观尺度之间的关系, 便于对复合材料的设计方案进行全方位的验证。
在对复合材料组织结构进行建模时, 常采用RVE 对纤维增强复合材料、 颗粒增强复合材料、纤维-颗粒混杂增强复合材料、编织复合材料和层合板等进行多尺度建模。RVE 是指包含复合材料中所有组分,即增强体和基体的最小体积单元,是微尺度响应均匀化导致宏观行为的域。 在建立RVE 模型时,应尽可能真实且完整地体现复合材料的微观组织特征。
对于几何结构较为简单的复合材料,Kou 等[38]在预测单向纤维增强复合材料的宏观力学参数时,建立了如图3 所示的单向纤维增强复合材料RVE模型,根据RVE 在各种载荷情况下纤维与基体之间的变形协调,提出了4 种变形协调因子,以提高预测精度。 对于纤维随机分布的复合材料,建立RVE 模型时需考虑更多的组织结构特征。 Koohbor 等[39]基于光学与扫描电镜数字图像相关测量相结合, 发展了一种纤维随机分布的碳纤维增强复合材料多尺度建模方法,有助于确定纤维增强复合材料RVE 模型的尺寸。 Uetsuji 等[40]基于渐进均匀化理论对纤维增强塑料的变形行为进行多尺度有限元分析, 采用随机顺序吸附算法构建了包含随机取向纤维的RVE模型,如图4 所示。 其中,AGf 为纤维聚集度,表明了纤维长径比和聚集程度对拉伸载荷下非线性响应的影响。 Yuan 等[41]利用纤维随机分布的RVE 建模方法, 提出了一种考虑聚合物杨氏模量随温度变化的改进内聚力模型来模拟碳纤维增强聚合物复合材料的界面行为, 通过对比横向力学性能的实验结果和模拟结果验证了模型的可靠性。 Catalanotti[42]采用增强体随机分布的RVE 快速建模方法,建立了一种长纤维或球形颗粒增强复合材料的微观力学模型,并使用几种统计空间描述符来评价粒子分布的良好性,如图5 所示。
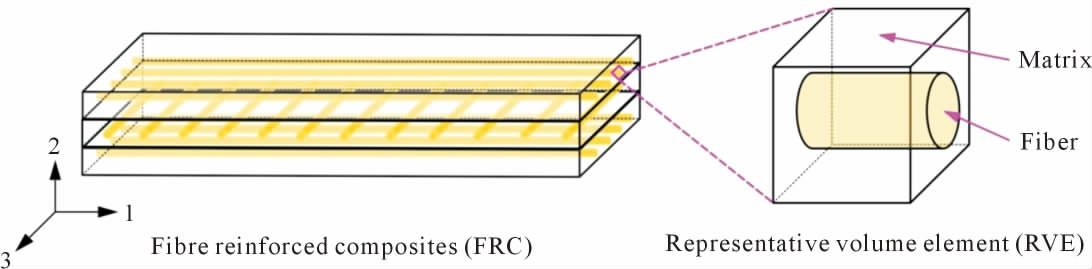
图3 单向纤维增强复合材料RVE[38]
Fig.3 RVE of unidirectional fibre reinforced composites[38]
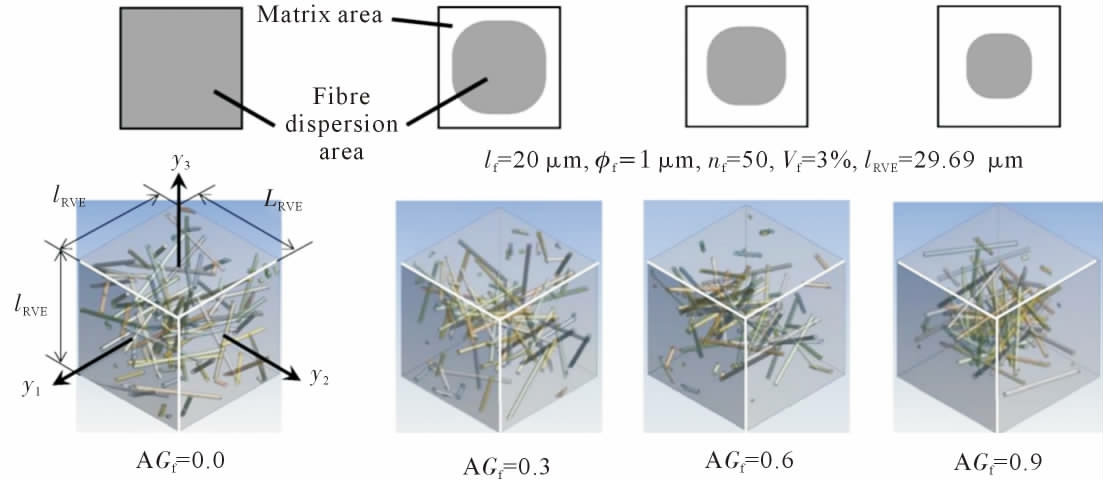
图4 不同纤维聚集度的随机分散RVE 模型[40]
Fig.4 Randomly dispersed RVE models with different fibre aggregation degrees[40]
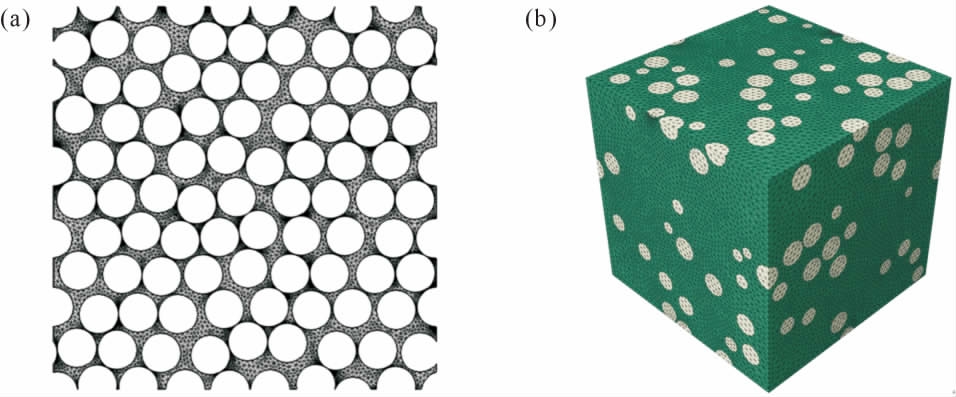
图5 采用生成随机分布均匀圆形或球形颗粒算法所构建的RVE 有限元模型:(a)二维RVE,(b)三维RVE[42]
Fig.5 RVE finite element models constructed by the algorithm for generating randomly distributed uniform circular or spherical particles:(a)2D RVE,(b)3D RVE[42]
对于具有复杂形状增强体的复合材料, 在建模时要同时考虑增强体的几何尺寸、 体积分数和分布的随机性。 Nakka 等[43]提出了一种不同形状夹杂物RVE 建模方法,生成的RVE 如图6 所示。
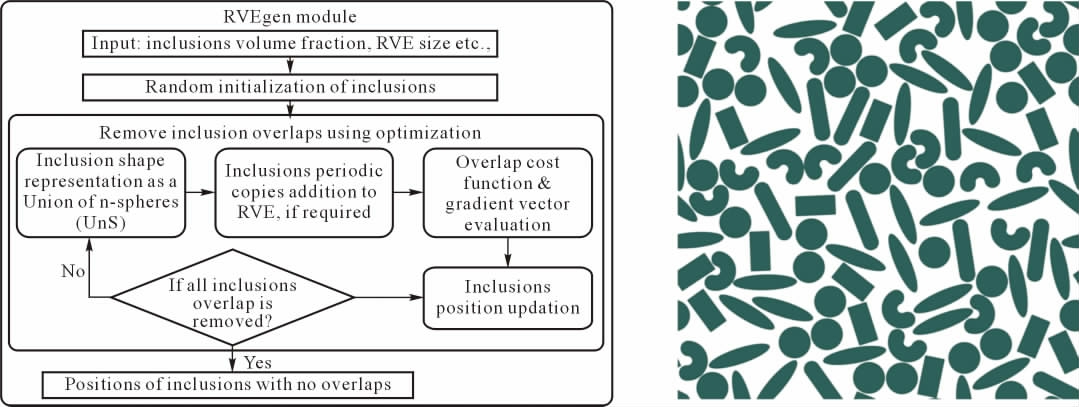
图6 RVE 生成流程图和不同夹杂物形状的样本RVE[43]
Fig.6 RVE generation flow chart and a sample RVE of different inclusion shapes[43]
在建立定向粒子增强复合材料的RVE 模型时,需要保证粒子取向的一致性。 Tian 等[44]对随机序列吸收算法进行了改进,包括粒子重定向算法、粒子交集检查算法、 粒子周期性约束算法和加速算法,从而能够高效地生成具有指定粒子取向的球形粒子增强复合材料的RVE,如图7 所示。
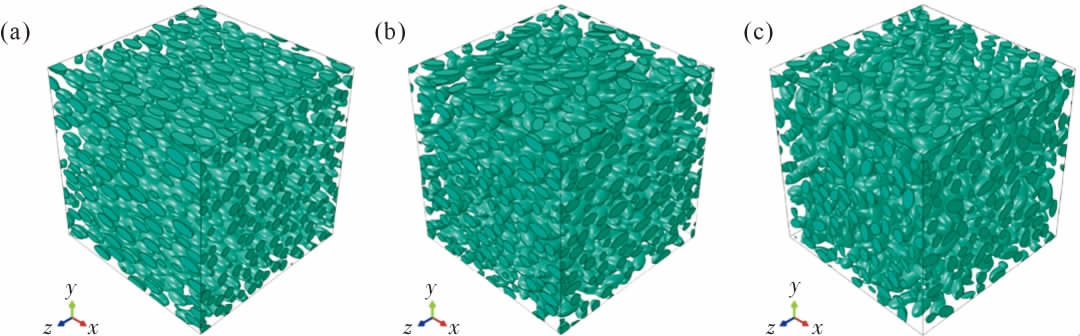
图7 不同颗粒取向a 复合材料的RVEs(增强体体积分数v1=30%, 颗粒数N=1 174):(a)a1D=diag(1.0,0.0,0.0),(b)a2D=diag(0.5,0.0,0.5),(c)a3D=diag(1/3,1/3,1/3)[44]
Fig.7 RVEs of the composites with v1=30%,N=1 174 and the different particle orientations:(a)a1D=diag(1.0,0.0,0.0),(b)a2D=diag(0.5,0.0,0.5),(c)a3D=diag(1/3,1/3,1/3)[44]
Peng 等[45]针对SiC 颗粒和CNTs 混杂增强铝基复合材料提出了一种多尺度数值计算方法,并根据实验结果建立了如图8 所示的考虑增强相几何形状和分布的SiC/CNTs-Al 复合材料微纳米尺度RVE,模拟了复合材料在单轴拉伸下的弹塑性变形、渐进损伤和断裂过程,实现了多尺度间的有效信息传递和混杂增强MMCs 的力学响应分析。
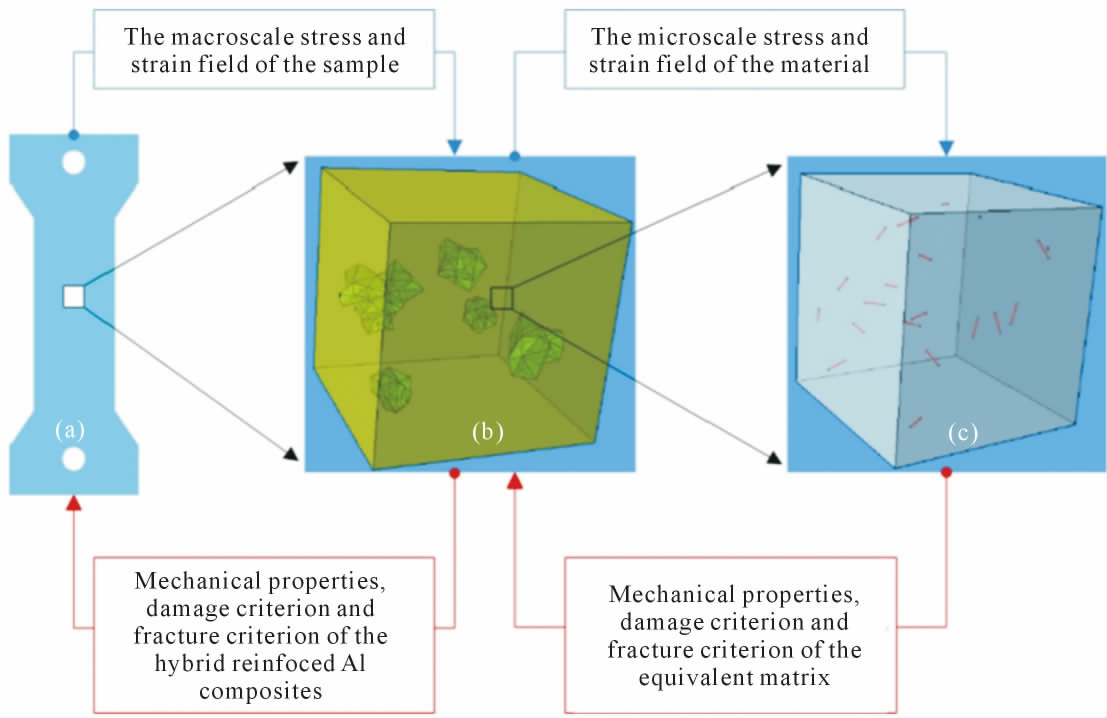
图8 多尺度分析方法的信息传递关系:(a)宏观尺度试样,(b)微观尺度RVE,(c)纳米尺度RVE[45]
Fig.8 Information transfer relationship of multi-scales analysis method:(a)macroscopic sample,(b)RVE at the microscale,(c)RVE at the nanoscale[45]
Rafiee 和Firouzbakht[46]在研究CNTs 增强聚合物复合材料时, 提出了一种分层多尺度建模方法。该建模方法是在宏观和介观尺度上分层建模,而在微观和纳米尺度上进行并行多尺度建模,将微纳尺度建模的结果作为输入信息输入到宏介观尺度,在保持CNTs 晶格结构的基础下, 实现了从基体到CNTs 的载荷传递,从而建立了多尺度之间的联系,如图9 所示。
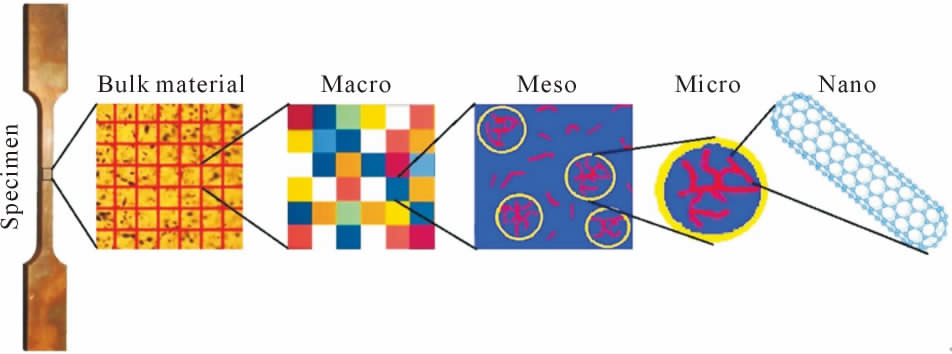
图9 CNTs 增强聚合物(CNTRP)的多尺度建模[46]
Fig.9 Multiscale modelling for CNT-reinforced polymers(CNTRP)[46]
Li 等[47]开发了一种采用超晶格RVE 的多尺度数值建模方法,如图10 所示。 该模型中,具有高刚度的纳米颗粒表现出纯弹性, 而有机相则呈现出Drucker-Prager 型弹塑性本构关系。 此外,敏感性研究表明, 超晶格内的小构型变化不会显著改变整体的刚度行为, 多尺度数值建模策略被证实适用于建立超晶格RVE 来模拟超晶体的纳米力学行为。
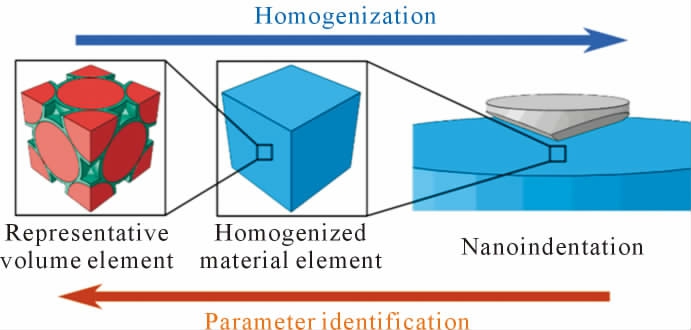
图10 参考纳米压痕测试实验结果,采用多尺度策略识别超晶格RVEs 中的界面相性质和超晶纳米复合材料的均匀化性质[47]
Fig.10 Multiscale strategy to identify interphase properties in RVEs of the superlattice and the homogenized properties of the supercrystalline nanocomposite,using experimental results from nanoindentation tests as reference[47]
对于纤维增强复合材料,Shi 等[48]提出了一种考虑了材料力学性能微观和介观参数分散性之间关系的多尺度随机模型, 研究了纤维增强复合材料的有效性能。 该模型中材料力学响应由多尺度随机有限元法获得,成功建立了有效性能与微/介观组分性能之间的关系。 Zhou 等[49]提出在多尺度框架下研究二维编织纤维增强陶瓷基复合材料损伤演化和性能分散的随机方法,模拟了材料在微/介观尺度下的损伤萌生和扩展过程, 证实了材料组织结构与有效力学性能之间存在显著关系。 Tang 等[50]在对短切碳纤维切屑增强复合材料的疲劳损伤行为进行实验和数值模拟研究时, 提出多尺度渐进损伤疲劳模型,在RVE 中加入了一种新的随机切屑填充算法和连续损伤模型。 Thapa 等[51]提出了一种用于碳纤维增强复合材料不确定性量化的多尺度模型框架, 首先利用非侵入式多项式混沌分解进行随机微尺度建模,得到受成分不确定性影响的层状材料有效性能,然后将这些随机有效性能与层合板的几何性能如层厚和层向的不确定性结合起来, 确定层合板的随机性能。Tian 等[52]采用多尺度均匀化方法,为了提高计算效率, 在宏观尺度上将层状复合材料理论与基于RVE 的有限元均匀化方法耦合, 预测了二维Cf/Mg复合材料的有效力学性能。
对于颗粒增强复合材料,Ahmadi 等[53]基于微观结构建立了能够预测颗粒增强复合材料的弹塑性变形和断裂机制的近场动力学模型, 考虑了颗粒形状与分布、基体塑性变形、颗粒-基体界面的损伤等因素,对于变形和损伤行为的评估更加可靠。 Zhang 等[54]提出了一种在混合-半并行多尺度框架下模拟多相材料中残余应力的三维多尺度方法, 一个宏观尺度模型通过尺度转换边界条件连接两个微观尺度模型,以SiCp/2124Al 复合材料为研究对象,对淬火残余应力进行了建模, 预测的基体和增强颗粒中的总残余应变与实验数据吻合较好。
鉴于复合材料的应用环境较为复杂, 同样可以采用数值模拟预测及优化复合材料在各种服役条件下的性能。 Izzi 等[55]提出了一种用于设计复合材料薄壁结构的多尺度优化策略, 将专用的全局-局部建模方法集成到多尺度两级优化策略中, 考虑作为设计变量的全套几何和力学参数, 定义了复合材料在每个相关尺度上的行为, 克服了基于分析或半经验模型的设计策略的多数局限性。Montesano 等[56]建立了基于物理机制的多尺度渐进损伤模型, 在连续损伤力学框架内耦合计算细观力学, 并通过商业有限元软件中的用户自定义子程序实现, 用于评估复合材料风力机叶片结构的亚临界损伤演化和刚度退化,具有预测复合材料关键区域损伤演变的能力,对提高损伤容限分析的精度和检验复合材料结构具有重要意义。 El Hachemi 等[57]提出了一种直观的计算多尺度均匀化的方法和工具, 用于估计复杂黏弹性复合材料和结构的力学性能, 开发的数值工具与ABAQUS 有限元分析相结合,以简化技术代码的获取,并允许精确和自动模拟复合材料工程结构,大大减少人为干预并合理控制误差。
4 结语和展望
近年来, 各种复合材料的数值模拟研究均取得显著进展,实现了对材料弹塑性变形、裂纹萌生与扩展、界面损伤与失效等行为的预测,为系统研究复合材料的力学性能提供了一种有效的途径, 对复合材料的设计和研发起到至关重要的促进作用。 由于CNTs/Al 复合材料较为复杂的组织结构和应用场景,在今后对其进行数值模拟研究时仍面临一些挑战:
(1)不同的数值模型在建模时的侧重点不尽相同,因此各自的适用范围有所不同,如何建立更加通用、全面、高精的复合材料数值模型具有挑战。
(2)新建立的基于物理机制的数值模型想要在商用有限元软件中得到运用,需要进行二次开发,数值模型在有限元软件中的嵌入程度及其实现效果有待验证。
(3)CNTs/Al 复合材料增强体与基体的界面行为非常复杂, 全面考虑其微观物理机制的数值模型仍有待建立。
上述问题如果能够在后续的研究中得以解决,不但可以发展CNTs/Al 复合材料的数值模拟技术,而且有利于更深入地了解CNTs/Al 复合材料微观组织与宏观性能的内在联系, 有助于组织结构设计和性能优化。
[1] KHANNA V,KUMAR V,BANSAL S A.Mechanical properties of aluminium-graphene/carbon nanotubes(CNTs) metal matrix composites: Advancement, opportunities and perspective[J]. Materials Research Bulletin,2021,138:111224.
[2] XU R, TAN Z Q, FAN G L, et al. Microstructure-based modeling on structure-mechanical property relationships in carbon nanotube/aluminum composites[J]. International Journal of Plasticity,2019,120:278-295.
[3] WAN J,CHEN B,FENG D,et al.Strengthening efficiency competition betweencarbonnanotubes (CNTs)andin-situAl4C3 nanorods in CNTs/Al composites influenced by alumina characteristics[J].Composites Part A: Applied Science and Manufacturing, 2022,152:106704.
[4] IACOBELLIS V,RADHI A,BEHDINAN K.A bridging cell multiscale modeling of carbon nanotube-reinforced aluminum nanocomposites[J].Composite Structures,2018,202:406-412.
[5] THIRUGNANASAMBANTHAM K G,SANKARAMOORTHY T,ANANTHA KISHAN A S, et al. Strengthening mechanisms of aluminium (Al) carbon nano tube (CNT) composites: A comprehensive review-Part 1[J].Materials Today: Proceedings,2022,60:1468-1473.
[6] CHEN J F,YAN L X,LIANG S Y,et al.Remarkable improvement of mechanical properties of layered CNTs/Al composites with Cu decorated on CNTs[J].Journal of Alloys and Compounds, 2022,901:163404.
[7] ZHOU L,LIU K Y,YUAN T B,et al.Investigation into the influence of CNTs configuration on the thermal expansion coefficient of CNT/Al composites[J].Journal of Materials Research and Technology,2022,18:3478-3491.
[8] DING C, YU K P, NODOOSHAN H R J, et al. Effect of powder microstructure on the thermal and mechanical properties of hot extruded Al-CNT composite[J].Journal of Alloys and Compounds,2022,891:162059.
[9] GUO Q, YAO W J, LI W B, et al. Constitutive models for the structural analysis of composite materials for the finite element analysis: A review of recent practices[J]. Composite Structures,2021,260:113267.
[10] SHETTY N,SHAHABAZ S M,SHARMA S S,et al.A review on finite element method for machining of composite materials[J].Composite Structures,2017,176:790-802.
[11] MISHNAEVSKY L JR.,BRØNDSTED P.Micromechanical modeling of damage and fracture of unidirectional fiber reinforced composites:A review[J].Computational Materials Science, 2009,44(4):1351-1359.
[12] HUANG J, RODRIGUE D. Equivalent continuum models of carbon nanotube reinforced polypropylene composites[J].Materials&Design,2013,50:936-945.
[13] WANG C Y,LIU Z L,XIA B,et al.Development of a new constitutive model considering the shearing effect for anisotropic progressive damage in fiber-reinforced composites[J].Composites Part B:Engineering,2015,75:288-297.
[14] DRABEK T, BÖHM H J. Damage models for studying ductile matrix failure in composites[J]. Computational Materials Science,2005,32(3-4):329-336.
[15] GURSON A L. Porous rigid-plastic materials containing rigid inclusions-yield function,plastic potential,and void nucleation:Proceedings of the international conference on fracture[C]. Oxford:Pergamon Press,1977.357-364.
[16] ROUSSELIER G.Ductile fracture models and their potential in local approach of fracture[J].Nuclear Engineering and Design,1987,105(1):97-111.
[17] JANG J, JEON S Y, CHOI J H, et al. Mechanical analysis of fiber-reinforced plastics using an elastoplastic-damage constitutive equation considering asymmetric material behavior[J]. Composite Structures,2021,272:114268.
[18] TANG T,HAMMI Y,HORSTEMEYER M F,et al.Finite element micromechanical analysis of the deformation and stress state dependent damage evolution in fiber reinforced metal matrix composites[J].Computational Materials Science,2012,59:165-173.
[19] VIGNJEVIC R, DJORDJEVIC N, GALKA A, et al. Constitutive model for fibre reinforced composites with progressive damage based on the spectral decomposition of material stiffness tensor[J].Composite Structures,2022,292:115596.
[20] ISMAR H, SCHRÖTER F, STREICHER F. Inelastic behavior of metal-matrix composites reinforced with fibres of silicon carbide,alumina or carbon: A finite-element analysis[J].Composites Science and Technology,2000,60(11):2129-2136.
[21] REINER J, FESER T, WAIMER M, et al. Axial crush simulation of composites using continuum damage mechanics: FE software and material model independent considerations[J]. Composites Part B:Engineering,2021,225:109284.
[22] VYAS G M,PINHO S T.Computational implementation of a novel constitutive model for multidirectional composites[J].Computational Materials Science,2012,51(1):217-224.
[23] HIRSCH F,NATKOWSKI E,KÄSTNER M.Modeling and simulation of interface failure in metal-composite hybrids [J].Composites Science and Technology,2021,214:108965.
[24] NGUYEN B N,KHALEEL M A.A mechanistic approach to damage in short-fiber composites based on micromechanical and continuum damage mechanics descriptions[J].Composites Science and Technology,2004,64(5):607-617.
[25] BARENBLATT G I, SALGANIK R L, CHEREPANOV G P. On the nonsteady propagation of cracks[J].Journal of Applied Mathematics and Mechanics,1962,26(2):469-477.
[26] GUO R,MAO L T,XIN Z Y, et al. Experimental characterization and micro-modeling of transverse tension behavior for unidirectional glass fibre-reinforced composite[J].Composites Science and Technology,2022,222:109359.
[27] HUI X Y, XU Y J, ZHANG W H. An integrated modeling of the curing process and transverse tensile damage of unidirectional CFRP composites[J].Composite Structures,2021,263:113681.
[28] LIU L Y,YANG Q S,LIU X,et al.Modeling damage evolution of graphene/aluminum composites considering crystal cracking and interface failure[J].Composite Structures,2021,267:113863.
[29] SHAO J C,XIAO B L,WANG Q Z,et al.An enhanced FEM model for particle size dependent flow strengthening and interface damage in particle reinforced metal matrix composites[J]. Composites Science and Technology,2011,71(1):39-45.
[30] ELTAHER M A, WAGIH A. Micromechanical modeling of damage in elasto-plastic nanocomposites using unit cell representative volume element and cohesive zone model[J]. Ceramics International,2020,46(8):10469-10480.
[31] KOTELNIKOVA-WEILER N, BAVEREL O, DUCOULOMBIER N, et al. Progressive damage of a unidirectional composite with a viscoelastic matrix, observations and modelling[J]. Composite Structures,2018,188:297-312.
[32] WENG L,FAN T X,WEN M,et al.Three-dimensional multi-particle FE model and effects of interface damage, particle size and morphology on tensile behavior of particle reinforced composites[J].Composite Structures,2019,209:590-605.
[33] HEIDE-JØRGENSEN S, BUDZIK M K, IBSEN C H. Three-dimensional, multiscale homogenization for hybrid woven composites with fiber-matrix debonding[J].Composites Science and Technology,2022,218:109204.
[34] LI X,CHEN J.A highly efficient prediction of delamination migration in laminated composites using the extended cohesive damage model[J].Composite Structures,2017,160:712-721.
[35] MASSARWA E, ABOUDI J, HAJ-ALI R. A multiscale modeling for failure predictions of fiber reinforced composite laminates[J].Composites Part B:Engineering,2019,175:107166.
[36] SKOVSGAARD S P H, HEIDE-JØRGENSEN S. Three-dimensional mechanical behavior of composite with fibre-matrix delamination through homogenization of micro-structure[J]. Composite Structures,2021,275:114418.
[37] FU C,WANG X.Prediction of the cohesive strength for simulating composite delamination by a micro-mechanical model based on random RVE[J].Composite Structures,2021,262:113343.
[38] KOU G J,ZHANG W,CHEN J S,et al.An improved rule of mixture model based on deformation coordination in predicting engineering constants of unidirectional fiber reinforced composites[J].Materials Today Communications,2023,34:105072.
[39] KOOHBOR B, MONTGOMERY C B, SOTTOS N R. Identification of RVE length scale in fiber composites via combined optical and SEM digital image correlation[J].Composites Science and Technology,2022,227:109613.
[40] UETSUJI Y, YASUDA S, TERAMOTO Y. Effect of fibre aspect ratio and aggregation on nonlinear material property of random cellulose reinforced composites:A multiscale computational study[J].Composite Structures,2022,301:116201.
[41] YUAN X W, LI W G, XIAO Z M, et al. Prediction of temperature-dependent transverse strength of carbon fiber reinforced polymer composites by a modified cohesive zone model[J].Composite Structures,2023,304:116310.
[42] CATALANOTTI G. On the generation of RVE-based models of composites reinforced with long fibres or spherical particles[J].Composite Structures,2016,138:84-95.
[43] NAKKA R,HARURSAMPATH D,PATHAN M,et al.A computationally efficient approach for generating RVEs of various inclusion/fibre shapes[J].Composite Structures,2022,291:115560.
[44] TIAN W L, CHAO X J, FU M W, et al. An advanced method for efficiently generating composite RVEs with specified particle orientation[J].Composites Science and Technology, 2021,205:108647.
[45] PENG Y H,ZHAO H T,YE J R,et al.Multiscale 3D finite element analysis of aluminum matrix composites with nanoµ hybrid inclusions[J].Composite Structures,2022,288:115425.
[46] RAFIEE R,FIROUZBAKHT V.Stochastic multiscale modeling of CNT/polymer[M]//RAFIEE R.Carbon Nanotube-reinforced polymers.Amsterdam:Elsevier,2018:503-520.
[47] LI M J,SCHEIDER I,BOR B,et al.Ultra-thin and ultra-strong organic interphase in nanocomposites with supercrystalline particle arrangement: Mechanical behavior identification via multiscale numerical modeling[J].Composites Science and Technology,2020,198:108283.
[48] SHI D Q,TENG X F,JING X,et al.A multi-scale stochastic model for damage analysis and performance dispersion study of a 2.5D fiber-reinforced ceramic matrix composites[J]. Composite Structures,2020,248:112549.
[49] ZHOU L C, CHEN M W, LIU C, et al. A multi-scale stochastic fracture model for characterizing the tensile behavior of 2D woven composites[J].Composite Structures,2018,204:536-547.
[50] TANG H B,ZHOU G W,CHEN Z X,et al.Fatigue behavior analysis and multi-scale modelling of chopped carbon fiber chip-reinforced composites under tension-tension loading condition [J].Composite Structures,2019,215:85-97.
[51] THAPA M, MULANI S B, WALTERS R W. Stochastic multi-scale modeling of carbon fiber reinforced composites with polynomial chaos[J].Composite Structures,2019,213:82-97.
[52] TIAN W L,QI H L,CHAO X J,et al.Experimental and multi-scale numerical evaluations for effective mechanical properties of 2-D Cf/Mg composites[J].Composite Structures,2018,189:1-8.
[53] AHMADI M, SADIGHI M, HOSSEINI-TOUDESHKY H. Microstructure-based deformation and fracture modeling of particulate reinforced composites with ordinary state-based peridynamic theory[J].Composite Structures,2022,279:114734.
[54] ZHANG X X, XIAO B L, ANDRÄ H, et al. Multi-scale modeling of the macroscopic,elastic mismatch and thermal misfit stresses in metal matrix composites[J].Composite Structures,2015,125:176-187.
[55] IZZI M I, MONTEMURRO M, CATAPANO A, et al. A multi-scale two-level optimisation strategy integrating a global/local modelling approach for composite structures[J]. Composite Structures,2020,237:111908.
[56] MONTESANO J, CHU H, SINGH C V. Development of a physics-based multi-scale progressive damage model for assessing the durability of wind turbine blades[J]. Composite Structures,2016,141:50-62.
[57] EI HACHEMI M,KOUTSAWA Y,NASSER H,et al.An intuitive computational multi-scale methodology and tool for the dynamic modelling of viscoelastic composites and structures[J].Composite Structures,2016,144:131-137.