金属镁(Mg)、铝(Al)及其合金由于具有密度低、强度高、导热性良好等特点，而被广泛应用在国防工业、航空航天等领域，用于减轻结构质量、增强力学性能、提高散热效率等。 其重要优势在于能够提高武器的射程和命中精度，提高航空器和航天器的机动性能，降低火箭和飞船等的发射成本[1]。 目前，其应用范围包括各种军事装备的发动机零件、 支架结构以及火箭、导弹和卫星的一些零部件等。 例如，法国早期生产的MK50 反坦克枪榴弹的部分零件采用了Mg 合金和Al 合金[2]；美国M551“谢里登”轻型坦克/侦察车的变速箱体由Al-Mg 合金材料制成[3]。随着熔炼和制造技术的不断提高，Mg、Al 及其轻合金在坦克和装甲的部分结构件、导弹壳体和尾翼等方面将得到更加广泛的应用。
物态方程(equation of state,EOS)描述材料在不同温度和压强条件下的结构和热力学性质，在高压物理、地球物理和武器物理等涉及高温高压极端条件的领域中有重要应用价值。 而熔化曲线作为温度-压强相图中固液相各自稳定区域的分界线， 是建立材料固液多相EOS 的必要基础[4-5]。 研究Mg、Al 及其合金材料的高压熔化曲线，对于构建它们的固液多相EOS 模型， 进而支撑Mg、Al 合金材料高温高压下性能的优化设计，具有重要意义[6]。
对于Al 和Mg 的高压熔化曲线，以往已经开展了较多的实验和理论研究，其中实验测量达到的最高压强分别是125 GPa 和105 GPa。Hänström 等[7]和Boehler 等[8]在静态金刚石压砧(diamond anvil-cell,DAC)实验中，分别测量了Al 在50 GPa 和80 GPa以内的熔点，他们的结果相互符合较好。 Shaner 等[9]在冲击实验中，测量了Al 在125 GPa 附近的熔化温度，结果与静态实验[7-8]的高压外推值符合较好。 与Al 的情况不同，Mg 的高压熔化曲线存在较大争议。在20 GPa 以内，Mg 的不同静态实验结果之间具有较好的一致性[10-11]。Errandonea 等[12]和Stinton 等[13]在静态DAC 实验中， 测量了Mg 在80 GPa 和105 GPa下的熔化温度。在相对较低的压强下，Stinton 等[13]和Errandonea 等[12]给出的熔化曲线十分接近。 但当压强超过50 GPa 时，Stinton 等的熔化温度高于Errandonea 等的结果， 且二者之间的差异随压强升高而逐渐增大。 在105 GPa，Stinton 等的熔化温度(约4 400 K)比Errandonea 等熔化曲线的高压外推值(约3 600 K)高约800 K。 近期，Beason 等[14-15]开展了2 项Mg 的冲击实验研究工作，前者发现当压强为(55±2) GPa 时发生了冲击熔化[14]，后者发现冲击熔化的起始压强为(55.5±0.3)GPa[15]，这2 个冲击熔点的压力值高度一致。 基于不同的EOS 模型，Beason 等估计了相应的熔化温度， 一个结果位于2 550~3 120 K[14]，另一个结果为2 960 K[15]，这2 个结果低于相同压强下Errandonea 等[12]和Stinton 等[13]的静态实验结果(分别约为3 200 K 和3 300 K)。
对于由Mg 和Al 所组成的二元合金体系，以往的实验和理论研究中发现，常压下熔化温度会随着合金组分比例的改变而发生变化，并且相对于相应单质体系的熔化温度有所降低[16-17]。 可以预期，在高压下也很可能存在类似情况。然而，目前高压下的相关研究却十分匮乏。 因此，为了弥补这一不足，有必要研究组分变化如何影响Mg-Al 和Al-Mg 合金的高压熔化曲线。
本工作结合固溶无序结构建模的相似原子环境(similar atomic environment,SAE)方法，以及熔点模拟的固液共存法， 实现了低固溶合金高压熔点的第一性原理分子动力学模拟， 在此基础上初步研究了2 种低固溶Mg-Al 和Al-Mg 合金的高压熔点。 考虑的2 种低固溶合金， 一种是LF6Al， 其中Al 和Mg的原子数分别约占92%和6%，另一种是AZ31B，其中Mg 和Al 的原子数分别约占96%和3%。 对于这2 种合金，目前仅发现Urtiew 等[18]在冲击实验中测量了AZ31B 在约40~60 GPa 之间的高压熔点。通过将这2 种合金的计算结果与Mg、Al 单质的计算结果进行比较，初步分析组分变化对Mg-Al 和Al-Mg合金熔化温度的影响。
1 计算方法和细节
在开展LF6Al 和AZ31B 的高压熔点模拟之前，首先需要描述这2 种低固溶合金的无序结构。为此，我们利用相似原子环境方法[19-20]进行无序固溶合金的结构建模。 该方法基于对整体平均原子环境的描述， 建立一个相似函数用来刻画与完全无序或近程有序结构的偏差， 并通过优化相似函数来得到所需的完全无序或近程有序结构。 该方法是一种新型的无序固溶材料结构建模方法，能够快速、有效地建立各种无序固溶材料的结构模型。
本工作中用于模拟熔点的固液共存法[21-22]，要求建立一个方向上较长的超胞结构， 在此基础上构建模拟所需的固液共存初始构型。 对于LF6Al， 建立3×3×16 的面心立方(face-centered cubic,fcc)超胞结构，共包含576 个原子，其中Al 和Mg 的原子数占比约为12∶1，非常接近LF6Al 中的实际情况。 对于AZ31B，建立4×4×16 的体心立方(body-centered cubic,bcc)超胞结构，共包含512 个原子，其中Mg 和Al 的原子数占比为31∶1， 十分接近AZ31B 中的实际情况。对于低固溶合金，由于不同种类的原子数占比差异较大， 假如直接建立一个方向上较长的超胞结构，因SAE 方法无法直接考虑较长方向上的无序构型，可能会导致在此方向上出现原子聚集的情况。因此，先利用SAE 方法建立一个较小的超胞，再将若干个这样的较小超胞拼接成一个细长的较大超胞。 以LF6Al 为例，首先建立一个3×3×4 的较小超胞，如图1 所示。 再将4 个这样的较小超胞拼接成一个3×3×16 的较大超胞， 如图2 所示。 在本工作中，还计算了Al 单质的熔化曲线，用于与LF6Al 的计算结果进行对比， 其中Al 的结构建模选用与LF6Al 相同的3×3×16的fcc 超胞结构。
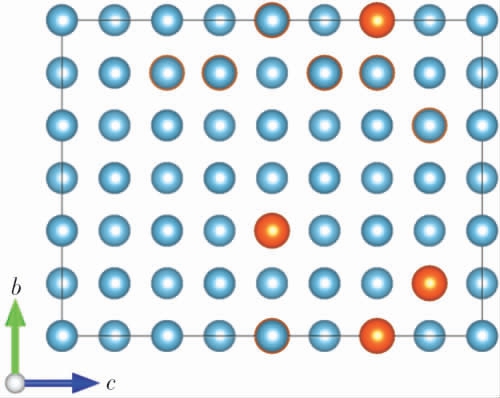
图1 LF6Al 的无序固溶结构，利用SAE 方法基于144 原子超胞产生
Fig.1 The disordered solid-solution structure for LF6Al,constructed by the SAE method based on a 144-atom supercell
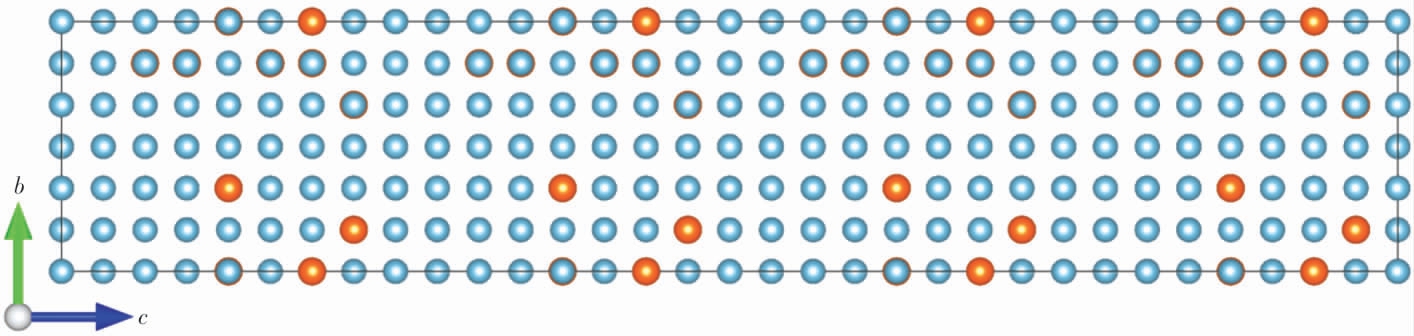
图2 LF6Al 的固溶无序结构，由图1 中的结构沿c 轴方向周期性扩展至4 倍长度给出
Fig.2 The disordered solid-solution structure for LF6Al,constructed by periodically repeating the structure in Fig.1 four times along the c direction
本工作中采用的固液共存法[21-23]，是一种基于分子动力学的高精度熔点模拟方法。 此方法通过搜索和模拟固液两相能够稳定共存的热力学状态， 并统计相应的温度和压强以给出熔点。 虽然在模拟中较容易实现， 但是一般需要考虑接近乃至超过千原子的较大体系， 导致相应的第一性原理计算模拟通常较为昂贵。在利用固液共存法模拟熔点时，通过采取如图3 所示的以下措施， 使得此方法能够基于较小体系在较短时间内得到精确结果, 兼顾计算效率和精度：
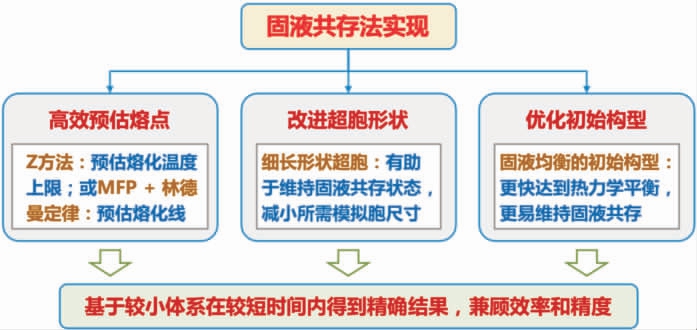
图3 本工作中对固液共存法的实现
Fig.3 Implementation of the solid-liquid coexistence method in this work
(1)高效预估熔点 这是为了限定熔点搜索的温度范围，以减少固液共存模拟的尝试次数。所考虑的预估方法有2 种：一是利用平均场势(mean-field potential,MFP)方法[24-25]，结合林德曼定律[26]，基于某个已知熔点和静态物态方程，快速给出高压熔化曲线；二是利用Z 方法[27]，基于小尺寸超胞开展分子动力学模拟，快速给出熔化温度上限(一般高估熔化温度10%左右)[28-29]。
(2)改进超胞形状 借鉴本研究组此前发展的更加适用于熔点经典分子动力学模拟的改进Z 方法[28]，将模拟胞选取为细长形状超胞。 如此，沿超胞的较长方向固液界面的移动存在更大空间，从而有助于在原子数较少的情况下维持固液共存状态，减小所需的模拟胞尺寸。
(3)优化初始构型 以往工作在应用固液共存法时，常常按照不同温度构建固液两部分的初始构型。 而本工作对于固液两部分，都按照预估的熔化温度进行构建，这样得到的初始构型更加均衡。 在固液共存模拟开始之后，不仅能在更短时间内达到热力学平衡，而且更有利于维持固液共存状态。
当准备好固溶无序构型并完成熔点预估之后，按照以下3 个步骤开展固液共存模拟：①固定晶格结构中的一半原子，先将温度升高到非常高的值(如两倍的预估熔化温度)以熔化另一半结构，再将温度逐渐降低到预估熔化温度；②解除原本固定的一半原子，同时固定另一半原子，将温度逐渐升高到预估熔化温度，从而获得固液相各一半的固液共存初始构型；③为了获得稳定的固液共存状态，将初始温度设置在预估熔化温度附近，对应于某个特定的能量E 值， 然后开展分子动力学模拟， 使体系在微正则(NVE)系综下演化到平衡。 对于所考虑的每个体积，都有一定的E 的范围，使体系能够保持固液共存状态达10 ps 或更长时间。 如果E 值低于该范围，则固液界面将会从固相部分向液相部分移动，即液相部分会凝固；如果E 值高于该范围，则固液界面将会从液相部分向固相部分移动，即固相部分会熔化；而当E 值处于该范围之内时，体系将演化为稳定的固液共存状态， 于是可以统计热力学平衡状态的温度和压强，以给出熔点。 假如E 值过高或过低，则可以不断地重复以上的第3 个步骤， 通过降低或提高初始温度来调整E 值， 直到给出稳定的固液共存状态。改变原子体积，重复上述步骤即可获得不同压强下的熔化温度。
在熔点模拟中， 需要识别体系在不同时刻所处的相态，即确定体系是处于固态、液态、还是固液共存状态。最简单的方法是直接观察体系的原子构型，其中有序和无序的结构部分分别对应于固相和液相。图4 展示了AZ31B 的熔点模拟中固液共存原子构型的一个实例。 此外，序参量[25,28,30]和数密度[30-32]的计算为定量识别固液相的结构提供了有效手段。 单个原子的局域序参量可通过下式定义为：
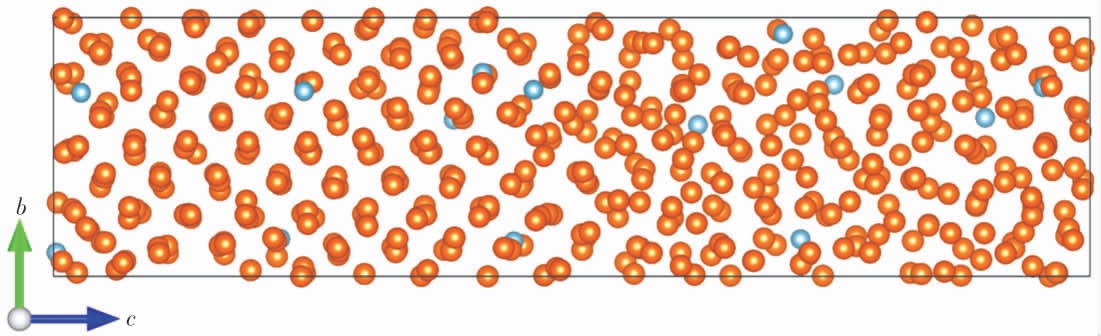
图4 AZ31B 熔点模拟中的一个固液共存构型
Fig.4 A solid-liquid coexistence configuration during the melting point simulation of AZ31B
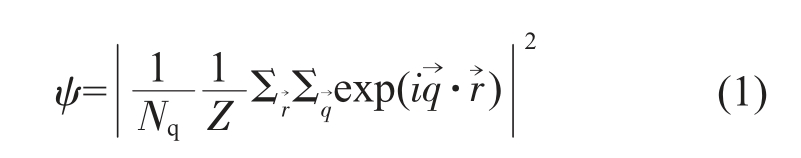
式中
为连接此原子与距其rc 范围内近邻原子之间的位移矢量，其中rc 的长度介于理想晶格中此原子与其2 个相邻的近邻壳层的距离之间，这2 个近邻壳层，对于fcc 结构可选择为第一和第二近邻， 对于bcc 结构可选择为第二和第三近邻；Z 为rc 距离范围内近邻原子的个数
为一系列波矢中的1 个，对于理想晶格中的任意
满足
为波矢
的个数。 为了降低序参量计算结果的较大波动，采用Morris 等[25]的方法，先是在较短的时间段内对瞬时原子位置进行平均之后再计算局域序参量， 然后与邻近原子的局域序参量进行平均以给出最终计算结果。 液相的序参量非常接近于0，这可以归结于液相的无序结构；而对于非零温下的晶体结构，序参量处于0~1 之间的某个数值附近。 数密度的计算方法是将体系切成垂直于超胞长边的等距切片， 并计算每个切片中的原子数量。数密度在体系的固相部分展现出强烈的周期性振荡，而在液相部分只表现出较小幅度的振荡。通过计算和分析不同时刻的序参量和数密度， 能够表征体系在模拟过程中固液相的比例及固液界面的位置随时间的演化情况。 图5 展示了AZ31B 的熔点模拟中序参量和数密度的一个计算实例。
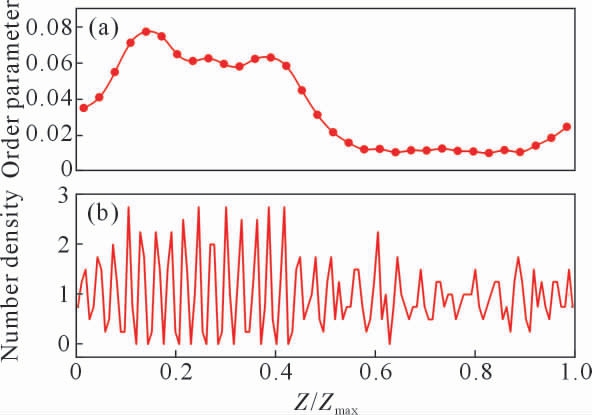
图5 AZ31B 的结构分析，与图4 中的原子构型对相应：(a)序参量；(b)数密度(除以了平均值)
Fig.5 Structure analyses for AZ31B,corresponding to the atomic configuration in Fig.4:(a)order parameter,(b)number density(divided by its average value)
本工作使用VASP (Vienna Ab-initio Simulation Package)软件[33-35]开展第一性原理计算模拟，采用全电子投影缀加波(projector augmented-wave,PAW)方法[36]处理离子实与价电子之间的相互作用，并利用广义梯度近似 (generalized-gradient approximation,GGA)的Perdew-Burke-Emzerhof (PBE)形式[37]描述交换关联相互作用。在所有计算中，平面波截断能均设置为600 eV， 大于所选Mg 和Al 赝势默认值(Mg_pv:403.929 eV，Al:240.3 eV)的1.5 倍。 在所选赝势中，Mg 和Al 的价电子组态分别为3s23p6 和3s23p1。对于熔点的固液共存模拟，采用NVE 系综开展分子动力学计算，其中时间步长选取为1 fs，总的模拟步数至少为5 000 步。
2 结果与讨论
2.1 LF6Al 合金的高压熔点
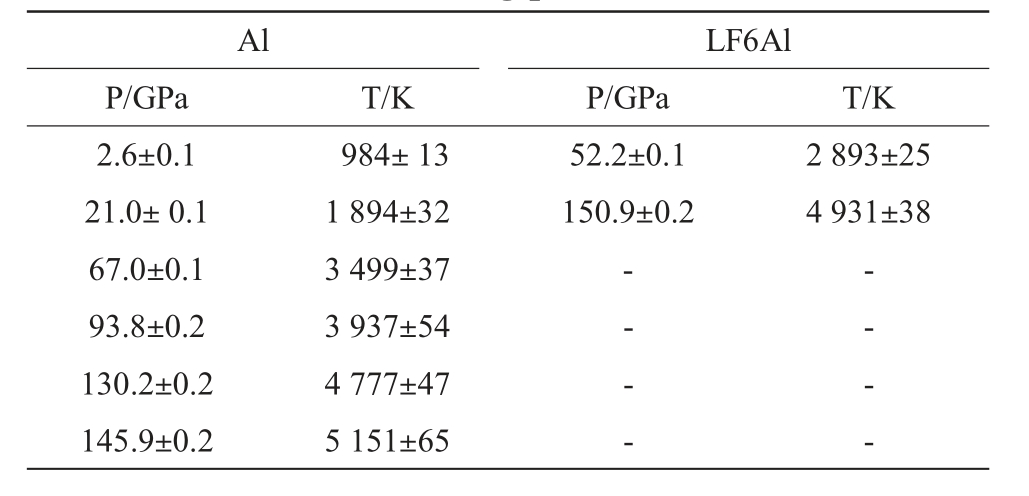
目前，公开文献中未见任何有关LF6Al 合金(Al和Mg 的原子数分别约占92%和6%)高压熔点研究的报道。 为了给LF6Al 的高压熔点模拟结果提供参照，我们利用固液共存法计算了150 GPa 以内Al 单质的熔化温度(Tm)，并与实验数据进行了比较，如图6(a)所示。 计算得到的Al 的熔化温度随压强的变化关系，能够很好地利用Simon-Glatzel 方程[38]表示如下：
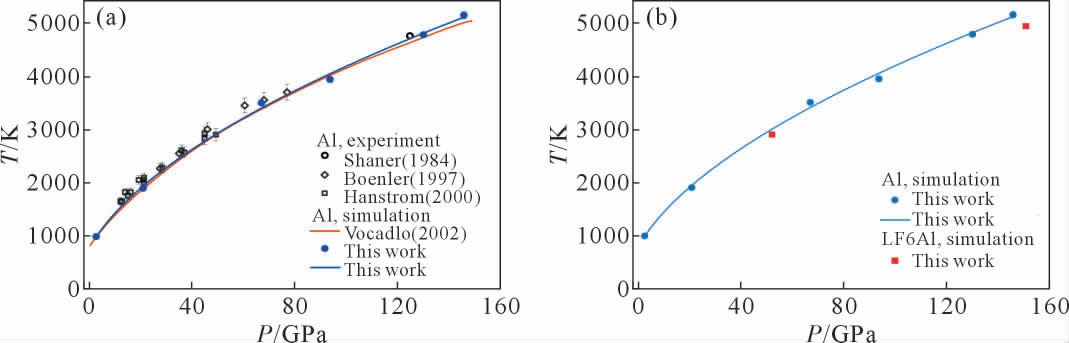
图6 Al 和LF6Al 的高压熔化：(a)Al 的熔点和熔化曲线，(b)LF6Al 的熔点
Fig.6 High-pressure melting of Al and LF6Al:(a)melting points and melting curve of Al,(b)melting points of LF6Al
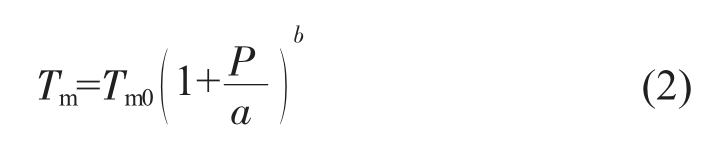
式中，Tm0、a 和b 为拟合参数。前面已经介绍过，对于Al 的熔化曲线， 实验测量达到的最高压强为125 GPa。 其中，Hänström 等[7]和Boehler 等[8]在静态DAC 实验中分别测量了50 GPa 和80 GPa 以内的熔点，他们的结果符合较好。Shaner 等[9]在冲击实验中测量了125 GPa 附近的熔化温度。 此外，Vocˇadlo 等[39]基于第一性原理计算， 利用热力学积分方法计算了Al 在150 GPa 以内的熔化曲线。 与此前Al 的研究相比， 我们的计算结果十分接近上述3 个实验的熔化温度下限；在100 GPa 以内，我们的熔化曲线与Vocˇadlo 等的计算结果几乎重合， 而在100~150 GPa之间，我们的熔化温度与Vocˇadlo 等的结果最大差异仅为约100 K。
我们利用固液共存法模拟了LF6Al 的2 个熔点，分别对应于相对较低和较高的2 个压强，并将其与Al 的计算结果进行了对比，如图6(b)所示。 表1展示了我们得到的Al 和LF6Al 的高压熔点计算结果。 如前所述，对于LF6Al，实际模拟中Al 和Mg 的原子数占比约为12∶1，十分接近LF6Al 中的实际情况。 可以看到，相同压强下LF6Al 的熔化温度计算结果低于Al 的计算结果，但仅仅略低了不超过10%，这与常压下的情况类似。 常压下Al 的熔化温度为933 K[40]，而根据以往Mg-Al 合金温度-组分相图的实验和理论研究， 常压下LF6Al 的熔化温度区间比Al 的熔化温度低出约30~90 K(约3.5%~9.5%)[16-17]。 这也就是说， 少量Mg 元素的存在使得从常压到高压的熔化温度都略微降低。 实际上，很多情况下合金的熔化温度都低于相应的主要金属组元的熔点[41-42]。这是因为不同金属组元的原子半径有所不同， 因此相对于纯金属来说形成稳定的晶格结构更加困难。 对于低固溶LF6Al 合金，从常压到高压的结果也符合这一情况。 另外，虽然常压下Mg 和Al 的熔化温度仅相差不到10 K[40]，高压下Mg 的熔化温度却明显低于Al，如100 GPa 时Mg 的计算结果比Al 低500 K以上， 这对高压下LF6Al 相对于Al 的熔化温度的降低也应有一定影响。
表1 Al 和LF6Al 的熔点计算结果
Tab.1 Calculated melting points of Al and LF6Al
?
2.2 AZ31B 合金的高压熔点
目前，公开文献中关于AZ31B 合金(Mg 和Al的原子数分别约占96%和3%)高压熔点研究的报道很少，Urtiew 等[18]在冲击实验中测量了约40~60 GPa之间的高压熔点。为了给AZ31B 高压熔点的模拟结果提供更多参照， 我们将其与Mg 单质的计算结果进行对比。在近期的工作中，本文的部分作者与合作者基于第一性原理分子动力学， 利用固液共存法计算了460 GPa 以内Mg 的熔化曲线[22]。 图7(a)展示了其中105 GPa 以内的计算结果，以及与实验数据的比较[22]。前面已经介绍，对于Mg 的熔化曲线，实验测量达到的最高压强为105 GPa。 在20 GPa 以内，我们的熔化曲线与Errandonea 等[11]和Courac 等[10]的静态实验测量结果符合较好。 在30~80 GPa 之间，Errandonea 等[12]在静态DAC 实验中测量的熔化温度比我们的计算结果平均偏高约300 K。 在105 GPa，Stinton 等[13]在静态DAC 实验中测量的熔化温度比Errandonea 等[12]的实验结果的高压外推值高约800 K，比我们的计算结果高约900 K。 高压下不同实验结果之间的较大差异，可能与所采用的判断熔化发生的标准不同有关[22]。值得注意的是，尽管在30 GPa 以上， 我们的熔化曲线明显低于Erran donea 等[12]和Stinton 等[13]的静态实验测量结果，但是当压强为55.5 GPa 时，我们预测的熔化温度(2 880 K)与近期Beason 等[15]在冲击实验研究中给出的值(2 960 K)非常接近。
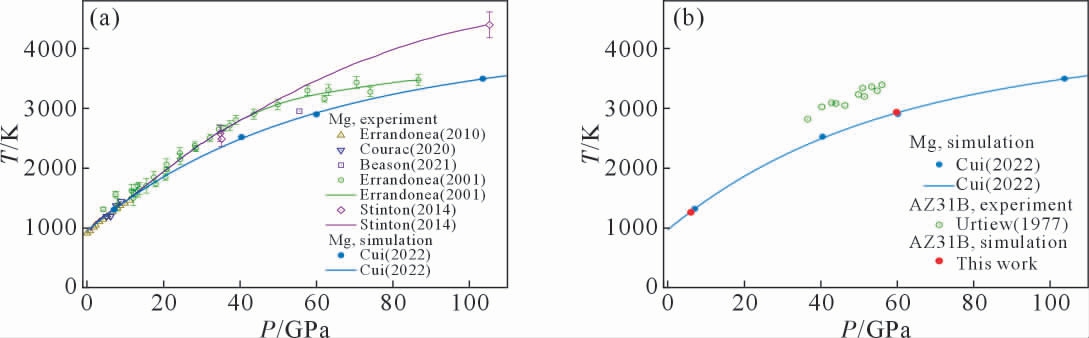
图7 Mg 和AZ31B 的高压熔化：(a)Mg 的熔点和熔化曲线，(b)AZ31B 的熔点
Fig.7 High-pressure melting of Mg and AZ31B:(a)melting points and melting curve of Mg,(b)melting points of AZ31B
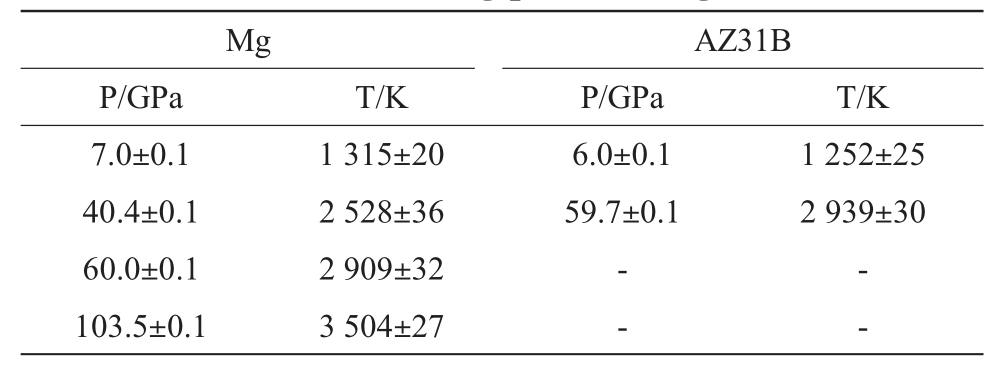
我们利用固液共存法模拟了AZ31B 的2 个熔点，分别对应于相对较低和较高的2 个压强，并将其与Mg 的计算结果以及AZ31B 的实验结果进行了对比，如图7(b)所示。 表2 展示了我们得到的Mg和AZ31B 的高压熔点计算结果。 如前所述， 对于AZ31B， 实际模拟中Mg 和Al 的原子数占比为31∶1，非常接近AZ31B 中的实际情况。 可以看到，相同压强下AZ31B 的熔化温度计算结果接近于Mg 的计算结果。 考虑到分子动力学给出的温度存在数十K 的不确定度，在此AZ31B 与Mg 的熔化温度高低实际上是难以区分的。 AZ31B 与Mg 的计算结果如此接近，与常压下的情况也十分类似。常压下Mg 的熔化温度为924 K[40]，而根据以往Mg-Al 合金温度-组分相图的实验和理论研究， 常压下AZ31B 的熔化温度区间比Mg 的熔化温度仅低出约10~25 K(约1%到3%)[16-17]。 从常压到高压AZ31B 与Mg 的熔化温度都很接近，可能是由于在AZ31B 中Al 原子数仅占约3%，因此熔化温度主要取决于Mg，而受Al的影响很小。 同时可以看到，在约40~60 GPa 之间，相比于Urtiew 等[18]的AZ31B 实验结果，Mg 和AZ31B的熔化温度计算结果都要偏低约15%(450 K 左右)。根据前面与图7(a)相关的讨论可知，数十GPa 以上高压下熔化温度的实验测量存在很大的不确定度。因此，为了准确给出高压下Mg 和AZ31B 的熔化温度，并确定两者之间的相对关系，还需进一步发展实验技术，开展更加精密的实验测量。
表2 Mg和AZ31B的熔点计算结果
Tab.2 Calculated melting points of Mg and AZ31B
?
3 结论
(1)结合固溶无序结构建模的相似原子环境方法，以及熔点模拟的固液共存法，实现了低固溶合金高压熔点的第一性原理分子动力学模拟。 其中，具体实现和初步研究了2 种低固溶Mg-Al 和Al-Mg 合金的高压熔点，这2 种合金分别是AZ31B(实际计算中Mg 和Al 的原子数占比为31∶1)和LF6Al(实际计算中Al 和Mg 的原子数占比约为12∶1)。
(2)通过将这2 种合金的计算结果与Mg、Al 单质的熔化曲线进行比较， 初步分析组分变化对Mg-Al 和Al-Mg 合金熔化温度的影响。 模拟发现，高压下LF6Al 的熔化温度略低于Al 的熔化温度，这可能由于LF6Al 的熔化温度取决于主要组元Al，同时受到少量Mg 存在的一定影响。 而高压下AZ31B 的熔化温度与Mg 十分接近，这可能是因为AZ31B 中Al 的原子数占比很小(仅为~3%)，因此Al 的影响很小，熔化温度基本是由主要组元Mg 来决定的。
本工作为后续深入研究合金组分变化对Mg-Al和Al-Mg 合金高压熔点的影响规律奠定了基础。
[1] 丁文江.镁合金科学与技术[M].北京：科学出版社，2007.DING W J.Science and technology in magnesium alloys[M].Beijing:Science Press,2007.
[2] KAYE A,STREET A.压铸冶金学[M].黄杏蓉，译. 北京：机械工业出版社，1987.KAYE A,STREET A. Die casting metallurgy[M].HUANG X R,translate.Beijing:China Machine Press,1987.
[3] 王军良.参加过海湾战争的M551 “谢里登” 空降/侦察坦克[J].国外坦克，2001(12):22-32.WANG J L. The Sheridan airborne/reconnaissance tank M551 in the Gulf War[J].Foreign Tank,2001(12):22-32.
[4] BENEDICT L X, OGITSU T, TRAVE A, et al. Calculations of high-pressure properties of beryllium : Construction of a multiphase equationofstate[J].PhysicalReviewB,2008,79(6):064106.
[5] REHN D A, GREEFF C W, BURAKOVSKY L, et al. Multiphase tin equation of state using density functional theory[J]. Physical Review B,2021,103(18):184102.
[6] 谭叶，肖元陆，薛桃，等. 镁铝合金的冲击熔化行为实验研究[J].高压物理学报，2019,33(2):39-44.TAN Y, XIAO Y L, XUE T, et al. Melting of MB2 alloy under shock compression[J]. Chinese Journal of High Pressure Physics,2019,33(2):39-44
[7] HÄNSTRÖM A,LAZOR P.High pressure melting and equation of state of aluminium[J].Journal of Alloys and Compounds, 2000,305(1-2):209-215.
[8] BOEHLER R,ROSS M.Melting curve of aluminum in a diamond cell to 0.8 Mbar: Implications for iron[J]. Earth and Planetary Science Letters,1997,153(3-4):223-227.
[9] SHANER J W,BROWN J M,MCQUEEN R G.Melting of metals above 100 GPa:High Pressure in Science and Technology[C].United States:Los Alamos National Lab,1984.126.
[10] COURAC A,LE GODEC Y,SOLOZHENKO V L,et al.Thermoelastic equation of state and melting of Mg metal at high pressure and high temperature[J].Journal of Applied Physics,2020,127(5):055903.
[11] ERRANDONEA D.The melting curve of ten metals up to 12 GPa and 1 600 K[J].Journal of Applied Physics,2010,108(3):033517.
[12] ERRANDONEA D, BOEHLER R, ROSS M. Melting of the alkaline-earth metals to 80 GPa[J].Physical Review B,2002,65(1):022108.
[13] STINTON G W, MACLEOD S G, CYNN H, et al. Equation of state and high-pressure/high-temperature phase diagram of magnesium[J].Physical Review B,2014,90(13):134105.
[14] BEASON M T,MANDAL A,JENSEN B J. Direct observation of the hcp-bcc phase transition and melting along the principal Hugoniot of Mg[J].Physical Review B,2020,101(2):024110.
[15] BEASON M T, JENSEN B J, CROCKETT S D. Shock melting and the hcp-bcc phase boundary of Mg under dynamic loading[J].Physical Review B,2021,104(14):144106.
[16] CHARTRAND P, PELTON A. Critical evaluation and optimization of the thermodynamic properties and phase diagrams of the AI-Mg,AI-Sr, Mg-Sr and AI-Mg-Sr systems[J].Journal of Phase Equilibria,1994,15(6):591-605.
[17] REN Y P,QIN G W,LI S,et al.Re-determination of γ/(γ+α-Mg)phase boundary and experimental evidence of R intermetallic compound existing at lower temperatures in the Mg-Al binary system[J].Journal of Alloys and Compounds,2012,540:210-214.
[18] URTIEW P A, GROVER R. The melting temperature of magnesium under shock loading[J].Journal of Applied Physics,1977,48(3):1122-1126.
[19] SONG H Q, TIAN F Y, HU Q M, et al. Local lattice distortion in high-entropy alloys[J].Physical Review Materials, 2017, 1(2):023404.
[20] TIAN F Y, LIN D Y, GAO X Y, et al. A structural modeling approach to solid solutions based on the similar atomic environment[J].Journal of Chemical Physics,2020,153(3):034101.
[21] ALFÈ D. Temperature of the inner-core boundary of the Earth:Melting of iron at high pressure from first-principles coexistence simulations[J].Physical Review B,2009,79(6):060101(R).
[22] CUI C F,XIAN J W,LIU H F,et al.Melting curve of magnesium up to 460 GPa from ab initio molecular dynamics simulations[J].Journal of Applied Physics,2022,131(19):195901.
[23] ZHANG T,WANG S,SONG H,et al.Melting curve of vanadium up to 470 GPa simulated by ab initio molecular dynamics[J].Journal of Applied Physics,2019,126(20):111507.
[24] WANG Y, LI L. Mean-field potential approach to thermodynamic properties of metal:Al as a prototype[J].Physical Review B,2000,62(1):196-202.
[25] MORRIS J R,SONG X Y. The melting lines of model systems calculated from coexistence simulations[J]. Journal of Chemical Physics,2002,116(21):9352-9358.
[26] WALLACE D C.Statistical physics of crystals and liquids:a guide to highly accurate equations of state[M].Singapore:World Scientific,2002.
[27] BELONOSHKO A B, SKORODUMOVA N V, ROSENGREN A,et al. Melting and critical superheating[J]. Physical Review B,2006,73(1):012201.
[28] WANG S C,ZHANG G M,LIU H F,et al.Modified Z method to calculate melting curve by molecular dynamics[J].The Journal of Chemical Physics,2013,138(13):134101.
[29] BOUCHET J, MAZEVET S, MORARD G, et al. Ab initio equation of state of iron up to 1 500 GPa[J].Physical Review B, 2013,87(9):094102.
[30] WANG S C,LIU H F,ZHANG G M,et al.High-pressure melting of tantalum from the modified Z method[J]. Journal of Applied Physics,2013,114(16):163514.
[31] LIU Z L,CAI L C,CHEN X R,et al.Molecular dynamics simulations of the melting curve of tantalum under pressure[J]. Physical Review B,2008,77(2):024103.
[32] ZENG Z Y,HU C E,CAI L C,et al.Molecular dynamics study of the melting curve of NiTi alloy under pressure[J].Journal of Applied Physics,2011,109(4):043503.
[33] KRESSE,FURTHMULLER.Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set[J].Physical Review B,Condensed matter,1996,54(16):11169-11686.
[34] KRESSE G, JOUBERT D. From ultrasoft pseudopotentials to the projector augmented-wave method[J]. Physical Review B, 1999,59(3):1758-1775.
[35] KRESSE G F J.Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set[J].Computational Materials Science,1996,6(1):15-50.
[36] BLÖCHL P E.Projector augmented-wave method[J].Physical Review B,1994,50(24):17953-17979.
[37] PERDEW J P,BURKE K,ERNZERHOF M.Generalized Gradient Approximation Made Simple[J].Physical Review Letters,1996,77(18):3865-3868.
[38] SIMON F,GLATZEL G.Bemerkungen zur Schmelzdruckkurve[J].Zeitschrift für Anorganische und Allgemeine Chemie, 1929, 178(1):309-316.
[39] VOCˇADLO L,ALFÈ D.Ab initio melting curve of the fcc phase of aluminum[J].Physical Review B,2002,65(21):214505.
[40] HAYNES W M,LIDE D R,BRUNO T J.CRC handbook of chemistry and physics[M].Florida:CRC Press,2016.
[41] MORARD G, ANDRAULT D, GUIGNOT N, et al. Melting of Fe-Ni-Si and Fe-Ni-S alloys at megabar pressures:implications for the core-mantle boundary temperature [J].Physics and Chemistry of Minerals,2011,38(10):767-776.
[42] ZHOU S H,NAPOLITANO R E.Phase stability for the Cu-Zr system:First-principles,experiments and solution-based modeling[J].Acta Materialia,2010,58(6):2186-2196.