TC4 钛合金由于其良好的机械性能，已经是航空、医疗、汽车等领域中的重要材料[1-3]。 超塑性是指材料在特定温度、应变率区间内可以达到很大伸长量而不发生断裂行为的性能[4]。 超塑成形技术常用于生产具有复杂几何结构的零件， 常见于三层板、四层板和点阵结构中。 有限元数值模拟是超塑成形加载路径设计中的一种有效手段[5]，根据虚拟试验结果寻找不同温度、应变率下的变形规律，可以低成本地得到超塑成形的工艺窗口。 因此，应用可靠的有限元手段来描述超塑变形过程是成形工艺研究的基础，同时显著提高数值模拟的有效性对描述该过程也非常重要，这也是本文关注的重点。
目前， 针对超塑成形过程中力学行为和变形规律的数值模拟已被广泛研究。其中，大量文献聚焦于材料成形性与成形工艺之间影响规律的研究， 尤其是针对复杂结构中成形极限的判断方法[6]。 然而，对于超塑变形中其复杂的变形机理所导致的结构件成形窗口判断的复杂问题却少有研究。在实际生产中，目前较为常用的数值模拟方法主要有2 种： 稳定性原则方法和成形极限图(forming limit diagrams,FLD)。Hart 的稳定性准则是一种常见的准则，而Ghosh 经过研究后发现Hart 并不具有普适性[7]。此外，由于不同的稳定性准则通常是在特定的本构模型的基础上建立的，导致超塑变形模型应变率影响的复杂性又为该方法带来了新的挑战。 因此，在研究塑性变形成形极限时，FLD 曲线受到了更多的青睐， 该曲线是基于Hill 失稳准则和Swift 失稳准则而建立的[8]，综合考虑了超塑变形应变率的影响。Kröhn 等[9]将传统的FLD 技术扩展到超塑成形工艺中，并利用超塑成形极限图 (superplastic forming limit diagrams,SPFLD)研究了胀形超塑性过程的塑性稳定性。 此外，Alabort 等[10]针对三层空心结构采用SPFLD 进行成形极限分析， 进一步验证了该方法的有效性。同时，在针对三层结构成形过程的研究中，还充分利用多尺度数值模拟技术，以考虑成形过程中晶粒尺寸与空洞体积分数的演变，即在仿真成形过程中不仅考虑了宏观力学性能与结构之间的关系，还考虑了其微观组织的演变规律。 因此，这种方案能更加全面地探究结构件成形工艺，本课题组也对这一方法进行了探索[11]。在数值模拟过程中，材料的硬化规律采用CREEP 蠕变子程序进行表征[5]，虽然该模型已经被广泛应用于超塑成形数值模拟过程[12]，但其最大的弊端就是只能捕捉材料稳定变化时的流变行为。 Du 等[13]在对该结构进行超塑成形处理时，发现材料在变形过程中其晶粒发生了明显的生长现象，变形后材料的平均晶粒尺寸从5 μm 增加到10 μm，这本质上是应变影响的结果。Alabort 等[10]在处理这一问题时将参数进行了拟合，这种方法思路比较简单， 但是存在求解过程中计算量过大等问题，且容易引起应力表征出现硬化规律表征时的波动情况。 因此，有必要建立一种针对多尺度数值模拟中硬化规律的表征方法，进而提高仿真的有效性。
基于以上分析和讨论，本文根据材料的流变行为对其硬化规律进行表征，随后将其应用于多尺度数值模拟中， 对材料的超塑成形过程进行仿真，进而验证该方法的有效性。
1 超塑变形力学性能表征
1.1 高温拉伸实验
本研究采用的实验材料为1.0 mm 厚的TC4钛合金板材。 高温拉伸试验在岛津电子万能试验机(AG-Xplns100KN)上进行，该设备可实现室温~1 100 ℃区间内的拉伸试验， 最大拉应力为100 kN，拉伸速率为0.001~800.000 mm/min。加热炉有3 个加热区，分别由3 个热电偶测量温度，并由闭环温控系统实现控温， 保证试件在试验过程中保持所需的温度， 以满足实验设计的要求。 本试验温度为920 ℃，初始应变率采用10-4/s、10-3/s 和10-2/s 3 种应变速率，该变形条件下TC4 材料具有良好的超塑性能[14]。 试样以20 ℃/s 升温到设定温度，随后保温15 min，以确保材料组织和试样温度的均匀性，然后按设定温度和应变率进行高温拉伸试验。 拉伸后的流变应力曲线如图1 所示。
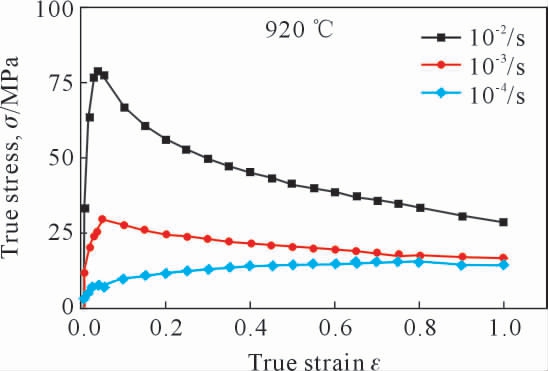
图1 TC4 合金高温拉伸试验流变曲线
Fig.1 The flow behavior of the TC4 alloy by high-temperature tensile tests
由图1 可知，TC4 合金在热变形初期，当初始应变率为10-2/s 时，合金的流变应力随其变形程度的增大而快速上升，在达到其峰值后迅速下降，而后下降趋势减缓， 直至实验结束。 当初始应变率为10-4/s 和10-3/s 时， 合金流变应力随着变形程度的增加而显著上升， 在达到最大值后逐渐趋于稳定直至实验结束，表明TC4 合金有一定的应变强化效应。 此外，图1 所示为在相同温度下，当应变速率从10-4/s升至10-2/s 过程中， 真应变-真应力曲线呈上升趋势，表明TC4 合金有一定的应变率强化效应，可知TC4 合金为明显应变速率敏感材料。
1.2 蠕变子程序硬化关系建模
对于超塑变形过程而言， 材料的应力应变关系通常采用下式进行描述：
式中，σ 为流动应力；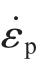
为应变速率；k 为材料系数；m 为应变速率敏感性指数，一般在0.3~0.9 之间。
有限元数值模拟是基于CREEP 蠕变子程序进行的，因此首先要确定模型中参数k 和m 的值。 对式(1)两边求对数可得式(2)，如下所示：
式中，σ 为真应力；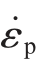
为真应变率。 m 和lnk 分别为
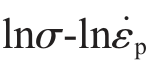线性拟合的斜率和截距，进一步计算可得不同应变下m 和k 的值， 如图2 中散点所示。 由图2可知， 在不考虑应变对材料力学性能影响的情况下， 采取二者的平均值进行计算， 其结果分别为
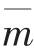=0.226，
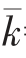=112.339。根据文献[15]中的研究结果，对于有软化特征的曲线进行定量描述时，其软化随应变演变的规律可用式（3）进行描述。 对于参数m 和k，其计算结果通过式（4）可得，其拟合结果如图2中曲线所示。
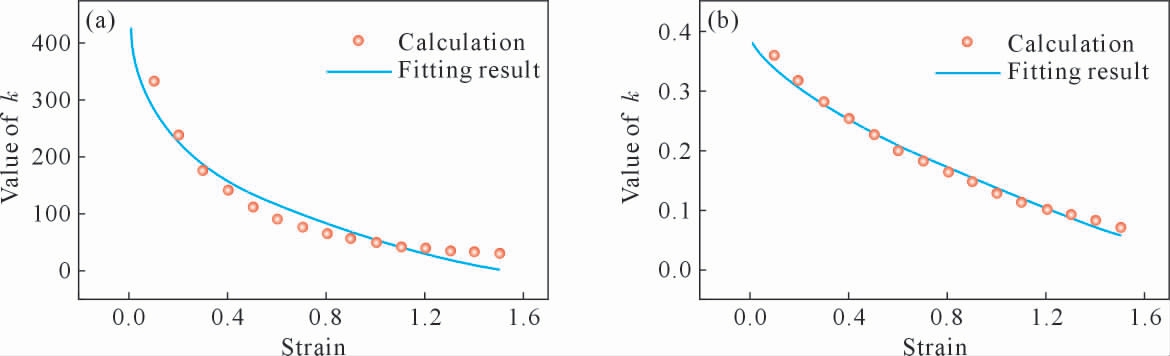
图2 模型中参数拟合结果：(a)k 值，(b)m 值
Fig.2 The parameter fitting results of the constitutive model:(a)value of k,(b)value of m
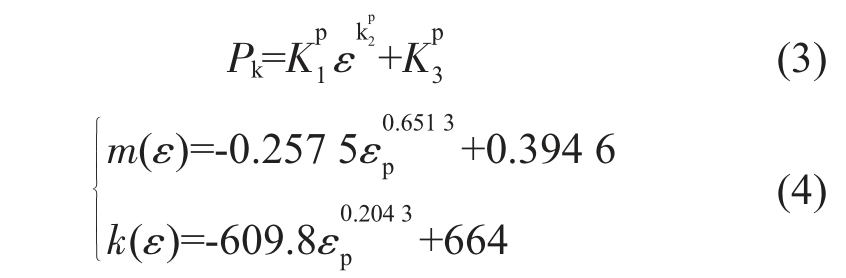
将式(4)带入到式(1)后，可以得到用于描述TC4合金超塑变形的本构模型，如式(5)所示：
本构模型的计算结果如图3(a)中实线所示，计算应力与实验结果之间相对吻合，则式(5)可以表征920 ℃时应力随应变率、应变的变化关系。 若不考虑应变的影响，模型可简化为：
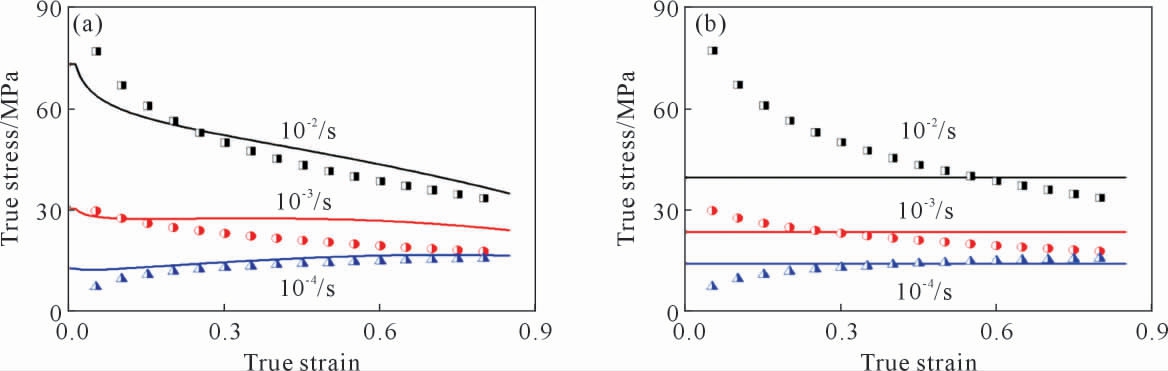
图3 本构模型计算结果与实验应力值的对比图：(a)考虑应变补偿，(b)不考虑应变补偿
Fig.3 Comparison between the calculated stress and experimental data:(a)considering strain compensation,(b)without considering strain compensation
模型对流变应力的描述如图3(b)中实线所示。此时应力计算结果并不随变形的进行而发生变化，始终保持为常数。
2 多尺度数值模拟
2.1 有限元模型
在有限元软件中， 建立恒应变速率高温拉伸试验中单拉试样的模型， 该模型来自于之前研究中所建立的模型[16]，如图4 所示。该拉伸实例中有限元模型涉及的本构模型采用用户定义材料， 用户材料选取蠕变子程序。 由于需要模型结果中应力试验值作为状态变量进行输出，因此，材料属性中需设置非独立变量为7，分别对应的是应变率、应变、应力、晶粒尺寸、位错密度、再结晶体积分数和空洞体积分数。本研究中，由于标距段内变形是均匀的，因此采用单元3038 的计算结果为代表，计算每个增量步中流变应力和微观内变量的结果。其中，内变量的计算结果采用之前研究的结果[17]。在有限元数值模拟时，对成形应变速率进行控制时， 其本质是依赖于对目标应变率进行控制加载。 在一个增量步中，新的载荷Pnew是根据控制变形区内所有积分点或单位集中等效应变率与目标应变率之间比值的最大值rmax 进行确定的，具体关系如式(7)所示[18]：
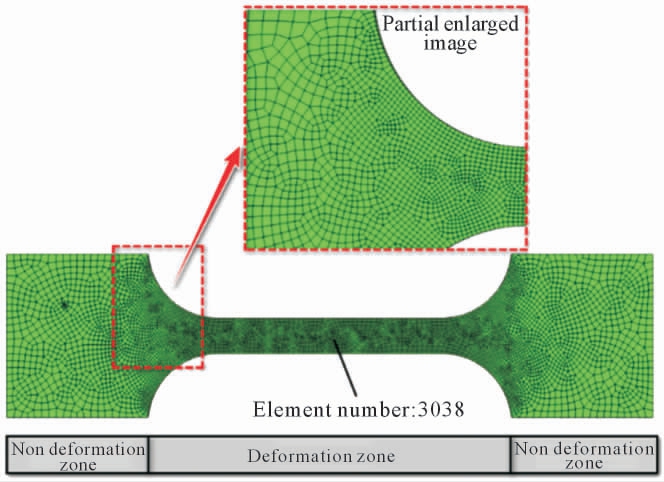
图4 有限元软件中的高温拉伸仿真模型[16]
Fig.4 Simulation model of the high temperature tensile test[16]
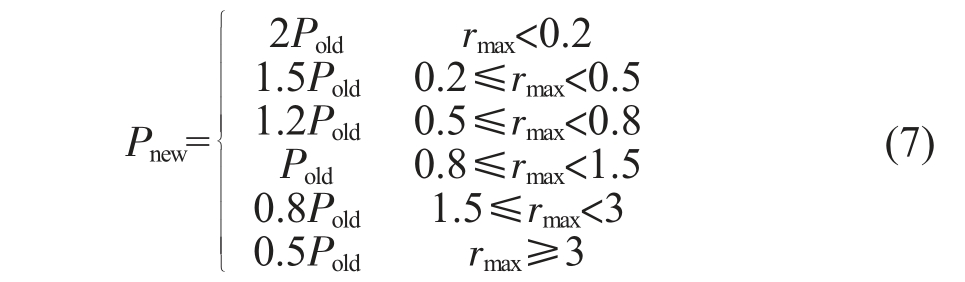
2.2 数值模拟有效性分析
2.2.1 流变应力仿真结果分析
对多尺度物理本构模型二次开发的有效性进行验证， 以温度920 ℃、 应变速率为10-2/s 的变形为例，不同时刻试样应力场模拟结果如图5 所示。由图5 可知，在高温拉伸试验时，变形主要发生在中间变形区，这与实际情况相符。 通过进一步分析可知，随着合金变形实验的进行， 材料在该变形条件下流变应力逐渐减小，出现了明显的应变软化现象，这也与高温拉伸试验的结果一致。
图5 高温拉伸过程数值模拟结果
Fig.5 Simulation results of the high temperature tensile test
为进一步验证流变应力数值模拟结果是否与高温拉伸实验数据一致， 本研究采用了考虑应变补偿和不考虑应变补偿的2 种硬化关系进行仿真， 单元3038 的模拟真应力与真应变的关系如图6 所示，散点为高温拉伸实验数据， 实线为考虑应变补偿的仿真结果，虚线为不考虑应变补偿的仿真结果。 由图6可知，采用应变补偿模型时，材料能够更为准确地描述流变应力的演变， 尤其当材料处于应力稳定区以外时，其影响结果更为显著。 因此，在基于蠕变子程序对材料超塑变形进行数值模拟时， 必须考虑应变对材料流变行为的影响， 蠕变子程序也应该是基于考虑应变补偿的模型而进行编写。
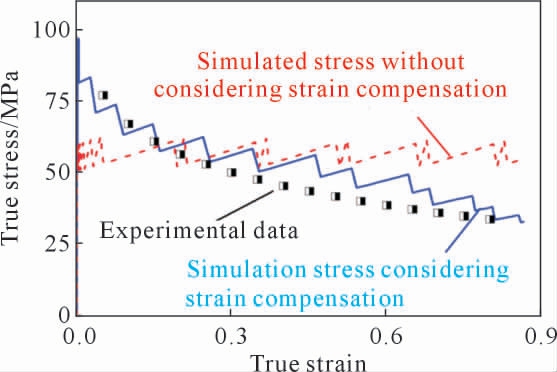
图6 流变应力模拟结果与实验值的对比
Fig.6 Comparison between the simulated stress and experimental data
2.2.2 微观组织仿真结果分析
高温拉伸试验模型3038 单元晶粒尺寸、空洞体积分数数值模拟结果与本构模型计算结果对比分别如图7 所示。散点为多尺度物理本构模型计算结果，线为有限元数值模拟计算结果。由图7 可知，数值模拟结果与本构模型计算结果的变化趋势一致， 且二者结果相差较小。由此可知，通过有限元数值模拟可以较为准确描述材料在超塑变形过程的微观组织变化。 此外，为进一步验证二次开发方法的有效性，本文对未进行高温拉伸试验的应变率2×10-3/s 和5×10-3/s 进行预测，结果如图8 所示。由图8 可知，数值模拟结果与本构模型计算结果产生了一定误差，但总体而言， 数值模拟计算结果仍然可以大致描述材料晶粒尺寸的演变规律， 表明这种二次开发的方法必要且有效。
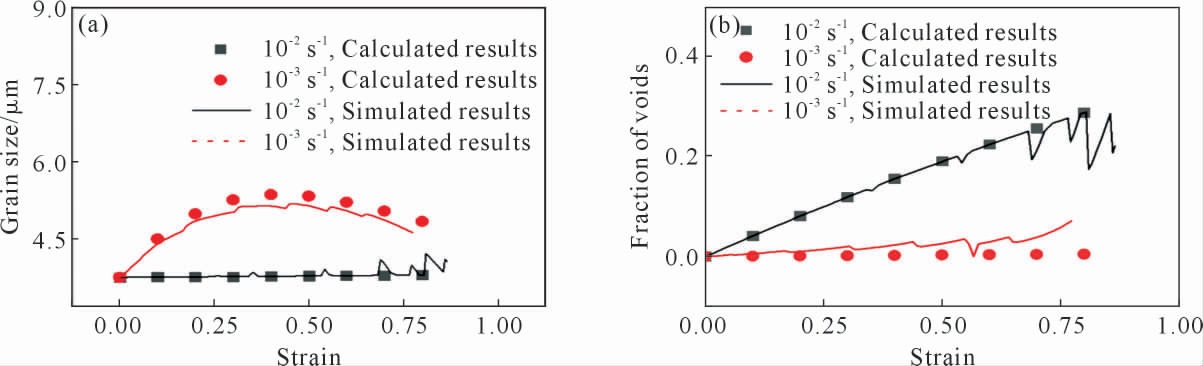
图7 内变量模拟结果与模型计算结果的对比：(a)晶粒尺寸，(b)空洞体积分数
Fig.7 Comparison between the simulated ISVs and calculated data by the constitutive model:(a)grain size,(b)volume fraction of voids
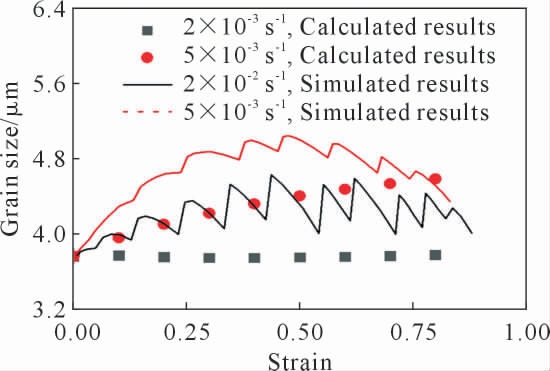
图8 晶粒尺寸模拟结果与模型计算结果的对比
Fig.8 The comparison between the simulated grain size and calculated data by the constitutive model
3 结论
(1)本文在超塑变形流变行为描述中考虑了硬化规律的影响，并建立了一套本构模型，将其应用于多尺度数值模拟中。
(2)考虑TC4 超塑变形应变补偿的模型应为：
(3)多尺度模拟结果中内变量的仿真结果与模型计算结果会有误差产生， 但总体上可以反应变形中晶粒尺寸的演变过程。
[1] SILVA L D,SIVASWAMY G,SUN L,et al.Effect of texture and mechanical anisotropy on flow behaviour in Ti-6Al-4V alloy under superplastic forming conditions[J]. Materials Science and Engineering:A,2021,819:141367.
[2] 王伟，宫鹏辉，史亚鸣，等. 轧制火次对EB 熔炼TC4 钛合金显微组织、织构和力学性能的影响[J]. 中国有色金属学报，2022,32(9):2595-2608.WANG W, GONG P H, SHI Y M, et al. Influence of hot rolling process on microstructure,microtexture and mechanical properties of Ti-6Al-4V alloy fabricated by electron beam cold hearth melting[J]. The Chinese Journal of Nonferrous Metals, 2022, 32(9):2595-2608.
[3] 韩飞，辛柏朴，刘冉. 钛合金板材辊弯成形特性及显微组织和织构演化规律[J].中国有色金属学报，2022:1-19.HAN F, XIN B P, LIU R. Roll forming characteristics and evolution law of microstructure and texture of titanium alloy sheet[J].The Chinese Journal of Nonferrous Metals,2022:1-19.
[4] LI G Y,DING H,ZHANG Y.Surface studies of superplasticity in Al-Zn-Mg-Cu alloy via in-situ tensile test[J]. Materials Science and Engineering:A,2022,841:1-5.
[5] WU Y,WU D P,MA J,et al.A physically based constitutive model of Ti-6Al-4 V and application in the SPF/DB process for a pyramid lattice sandwich panel[J]. Archives of Civil and Mechanical Engineering,2021,21:1-17.
[6] 赵祖德，窦小丽，王艳彬，等.Al6061/20SiCw 板材的超塑成形极限与空洞行为[J].中国有色金属学报，2009,19:235-240.ZHAO Z D,DOU X L,WANG Y B,et al. Forming limits and cavitation behaviors of superplastic Al6061/20SiCw sheet[J]. The Chinese Journal of Nonferrous Metals,2009,19:235-240.
[7] GHOSH A K. Tensile instability and necking in materials with strain hardening and strain-rate hardening[J]. Acta Metallurgica,1977,25(12):1413-1424.
[8] ZHU H H, HE Z B, LIN Y L, et al. The development of a novel forming limit diagram under nonlinear loading paths in tube hydroforming[J].International Journal of Mechanical Sciences,2020,172:105392.
[9] KRÖHN M A,LEEN S B,HYDE T H.A superplastic forming limit diagram concept for Ti-6Al-4V[J].Proceedings of the Institution of Mechanical Engineers,Part L:Journal of Materials:Design and Application,2007,221(4):251-264.
[10] ALABORT E,PUTMAN D,REED R C.Superplasticity inTi-6Al-4V:Characterisation, modelling and applications[J].Acta Materialia,2015,95:428-442.
[11] 杨东升.基于多尺度物理本构模型的TC4 超塑性成形工艺研究[D].西安：西北工业大学，2020.YANG D S. Research on superplastic forming process of TC4 based on mul-ti-scale physical constitutive model[D].Xi'an:Northwestern Polytechnical University,2020.
[12] LI G Y, TAN M J, LIEW K M. Three-dimensional modeling and simulation of superplastic forming[J]. Journal of Materials Processing Technology,2004,150(1-2):76-83.
[13] DU Z H,ZHANG K F.The superplastic forming/diffusion bonding and mechanical property of TA15 alloy for four-layer hollow structure with squad grid[J].International Journal of Material Forming,2021,14:1057-1066.
[14] YANG J Z,WU J J,ZHANG Q W,et al.Investigation of flow behavior and microstructure of Ti-6Al-4V with annealing treatment during superplastic forming[J]. Materials Science and Engineering:A,2020,797:140046.
[15] YANG J Z, WU J J, ZHANG Q W, et al. The simple hyperbolic-sine equation for superplastic deformation and parameters optimization[J].Journal of Materials Research and Technology,2020,9(5):10819-10829.
[16] 杨俊宙，吴建军.TC4 钛合金超塑成形流变行为[J]. 塑性工程学报，2022,29(1):140-146.YANG J Z, WU J J. Flow behavior of TC4 titanium alloy during superplastic forming[J].Journal of Plasticity Engineering, 2022,29(1):140-146.
[17] YANG J Z, WU J J, YANG D S, et al. A modified constitutive model with grain rotation for superplastic forming of Ti-6Al-4V Alloy[J].Journal of Engineering Materials and Technology,2020,142(2):1-13.
[18] YANG J Z, WU J J, ZHANG Q W, et al. Linear analysis of parameters in arrhenius model for Ti-6Al-4V at superplastic forming[J].Engineering Computations,2020,38(6):2528-2551.