在传统三维磁性材料中，随着温度的降低，热运动逐渐减弱，材料的磁性通常会在某个临界温度(居里温度Tc 或尼尔温度TN)发生磁相变，达到经典的三维长程磁有序(铁磁或反铁磁有序)。 而对于低维量子磁性材料，由于反铁磁性、低维性以及小自旋等因素，具有强烈的量子自旋涨落，使得其自旋在温度很低、甚至绝对零度下都能避免三维长程磁有序的出现，其基态一直处于自旋强纠缠下的高简并无序态，从而呈现出量子自旋液体、自旋轨道分离[1-4]、自旋能隙态[5-7]、spin-Peierls 相变[8-10]、波色-爱因斯坦(Bose-Einstein)相变[11-13]、磁化台阶[14-16]等丰富有趣的新奇量子现象。同时，由于低维量子磁性材料具有一维链或二维平面的结构特征， 其自旋量子涨落与同样具有低维结构的铜基、 铁基等非常规高温超导化合物的超导电性有很强的关联性[17-18]，在理解和解释超导机理方面也有着非常重要的科学意义。此外，低维量子磁性材料可以产生满足非对易统计、有能隙的分数化自旋激发，并且这种激发受长程量子纠缠的保护，使其不受局部微扰和噪声的影响，在容错拓扑量子计算、量子存储和量子传输等方面有广泛的应用前景[19-20]，是实现量子计算实用化的途径之一。 因此，低维量子磁性材料因具有量子自旋液体和自旋轨道分离等丰富有趣的新奇量子现象，与非常规高温超导的相关性以及在量子计算、量子存储和量子传输等方面的应用前景，引起了人们的极大关注，迅速成为研究前沿和热点[21-30]。
一维量子反铁磁性材料磁性相对较简单，因此首先得到重点关注和研究。 不同于链内和主磁交换作用均为铁磁性的单链磁体，一维量子反铁磁性材料的链内磁交换作用J 为反铁磁性作用， 可以产生强烈的量子自旋涨落，从而具有量子自旋液体等新奇量子现象。 2016 年，诺贝尔物理学奖获得者Haldane 教授曾提出一个著名的猜想[31]：半整数自旋(S=1/2,3/2,5/2…)和整数自旋(S=1,2,3…)一维量子反铁磁性链系统分别具有不同的量子无序基态。 当自旋为半整数时，自旋链系统低能激发无能隙，但可能存在spin-Peierls 相变，自旋—自旋两点间的关联函数随距离呈幂律形式衰减；当自旋为整数时，自旋链系统呈现出具有能隙的自旋单态，自旋—自旋两点间的关联函数随距离呈指数形式衰减。 随着研究的不断深入，Haldane 猜想很快得到了实验验证。Haldane 猜想的正确性改变了人们认为半整数自旋与整数自旋一维量子反铁磁性链情形定性相同的传统看法， 使许多科研工作者对一维量子反铁磁性链体系的研究产生了极大的兴趣[32]。 本文主要介绍了部分具有半整数和整数自旋的经典一维量子反铁磁性材料的制备方法、 晶体结构及其磁性能。
1 半整数自旋一维量子反铁磁性材料
根据Haldane 猜想， 具有半整数自旋的一维量子反铁磁性材料可能具有spin-Peierls 相变。 目前研究较多的具有半整数自旋的一维量子反铁磁性化合物主要包括TTF-MS4C4 (CF3)4 (TTF=四硫富瓦烯；M=Cu2+,Au2+)[33-35]、CuGeO3[36]、BaCu2Si2O7[37]、Cu3(CO3)2-(OH)2[15]、BaMn2V2O8[38]等，其中化合物TTF-MS4C4-(CF3)4 (M=Cu2+,Au2+)和CuGeO3 被发现存在spin-Peierls 相变，化合物BaCu2Si2O7 存在自旋偏转相变，化合物Cu3(CO3)2(OH)2 被发现具有1/3 磁化平台，而化合物BaMn2V2O8 被发现可能表现出经典磁性行为与量子磁性行为并存的现象。下面依次进行简单介绍。
化合物TTF-MS4C4(CF3)4(M=Cu2+, Au2+)最早被发现存在spin-Peierls 相变[33,35]。2 个化合物均通过在乙腈溶液中缓慢冷却得到。 TTF-CuS4C4(CF3)4 与TTF-AuS4C4(CF3)4 具有相同结构，均结晶于三斜晶系，空间群为P-1(图1)。 在其结构中，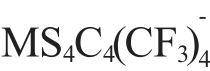
阴离子通过超交换相互作用沿c 轴形成一维磁性链[34]。如图2 所示，TTF-CuS4C4(CF3)4 与TTF-AuS4C4(CF3)4的磁化率分别在温度低于12 K 和2.1 K 时急剧下降， 表明这2 种化合物在相应温度发生了spin-Peierls相变。此时该链系统发生自旋晶格二聚化转变，单重基态与三重激发态分开，从而产生自旋能隙，体系经过相变后处于具有自旋能隙的非磁性基态[39]。
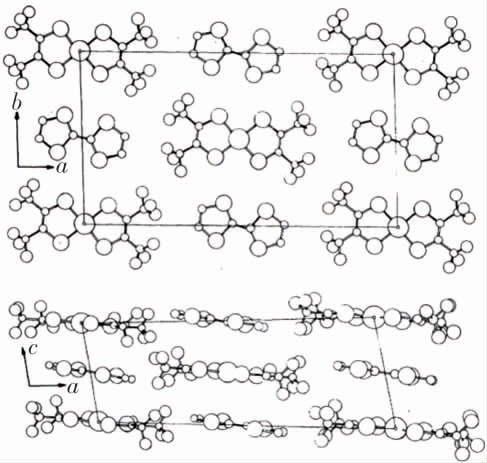
图1 TTF-CuS4C4(CF3)4 在ab 和ac 面上的晶体结构示意图[33]
Fig.1 The crystal structure of TTF-CuS4C4(CF3)4 viewed on the ab-plane and the ac-plane[33]
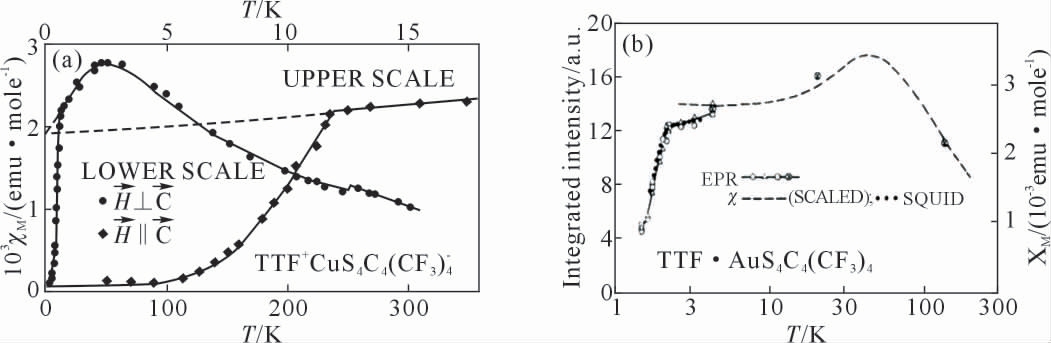
图2 磁化率随温度变化曲线：(a)TTF-CuS4C4(CF3)4,(b)TTF-AuS4C4(CF3)4[35]
Fig.2 Temperature dependence of magnetic susceptibilities:(a)TTF-CuS4C4(CF3)4,(b)TTF-AuS4C4(CF3)4[35]
CuGeO3 是首个被发现具有spin-Peierls 相变的无机化合物[8,36]，打破了科研工作者对spin-Peierls 相变在有机化合物中独有的认识，引起了科学界的轰动[40-44]。 该化合物最早由Völlenkle 等[45]通过在铂坩埚中高温烧结的方法合成得到。 CuGeO3 结晶于正交晶系，空间群为Pbmm。 常温下，Cu2+与4 个氧原子配位形成CuO4 平面，CuO4 基团通过共边连接沿c 轴延伸形成线性自旋链[45]。 如图3(a)所示，当温度降至14 K 时，CuGeO3 的结构发生了变化，GeO6 八面体角上的O1-O2 发生扭曲，变为四面体，Cu2+之间最近邻距离由2.942 Å 变为2.926 Å[46]。 磁化率随温度变化的曲线显示当温度低于14 K 时，磁化率在3个晶轴方向上都出现了急剧下降， 体系发生spin-Peierls 相变，形成二聚化的自旋能隙基态[47-52](图3(b))。 有趣的是，Li 等[53]研究发现CuGeO3 的尺寸和形貌与其spin-Peierls 相变之间存在着一定的关系。当CuGeO3 为纳米棒且长度小于600 nm 时不存在spin-Peierls 相变，而在长度大于600 nm 的纳米线中则可以出现较弱的spin-Peierls 相变。
图3 CuGeO3 的性质：(a)低温spin-Peierls 相的结构示意图,(b)在H=1 T 外场下单晶样品的磁化率随温度变化曲线[46,51]
Fig.3 The properties of CuGeO3:(a)schematic representation of the low-temperature structure in the spin-Peierls state,(b)temperature dependence of magnetic susceptibility for a single-crystal measured under H=1 T[46,51]
BaCu2Si2O7 是发生自旋偏转(spin-flop)相变的典型化合物[37,54-61]。 该化合物最早由Tsukada 等[54]通过常规固相反应得到， 并使用浮区法生长出直径为5 mm，长度为10 mm 的单晶棒样品。 在BaCu2Si2O7中，CuO4 平面通过O 原子以角连接的方式连接形成沿c 轴的一维自旋链(图4)。 如图5 所示[37]，对BaCu2Si2O7 外加一个沿c 轴方向的磁场， 随着磁场强度的增加，BaCu2Si2O7 的磁化强度线性增加。 当H=2.0 T 时，自旋发生偏转，磁化强度出现跳跃，体系的反铁磁相被破坏，形成了spin-flop1 相。 之后磁化强度继续随着场强增加而线性增加， 直至4.9 T时再次出现跳跃，体系进入spin-flop2 相。
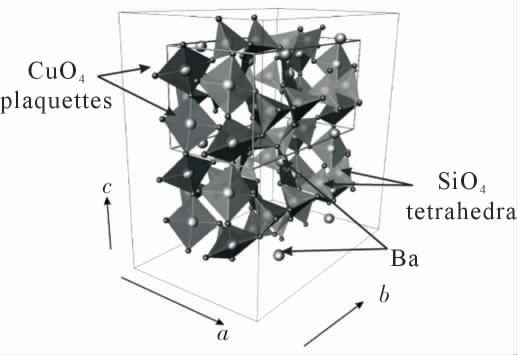
图4 BaCu2Si2O7 的晶体结构图[54]
Fig.4 The crystal structure of BaCu2Si2O754]
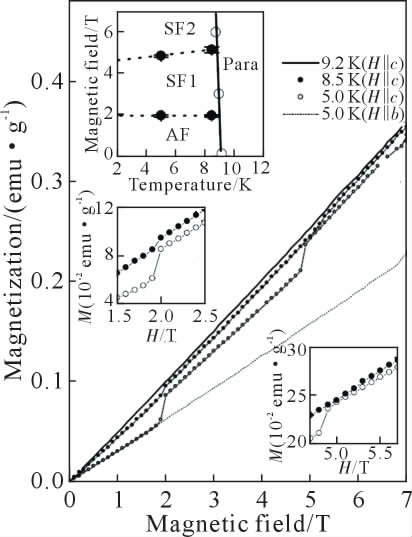
图5 BaCu2Si2O7 的磁化强度随外加磁场变化曲线[37]
Fig.5 Field dependence of the magnetization for BaCu2Si2O7[37]
具有1/3 磁化平台的一维金刚石链化合物Cu3-(CO3)2(OH)2 为天然矿物蓝铜矿，在此不再描述其合成方法。 该化合物结晶于单斜晶系，空间群为P21/c[62]。如图6(b)所示，自旋为S=1/2 的磁性金属Cu2+通过O 原子以角共享的方式连接， 从而形成沿b 轴无限延伸的一维磁性链。 在磁性链中存在J1、J2 和J3 3 种自旋耦合交换作用，由于J2>>J1、J3，因此J1 和J3 可以忽略不计(图6(a))。 图6(c)为Cu3(CO3)2(OH)2 的等温磁化强度随磁场变化曲线。 在低场处，化合物的磁化强度随着外加磁场的增大而线性增加， 直至H=11 T 时， 产生J2 自旋耦合交换作用的2 个Cu2+离子的自旋发生二聚化耦合，磁矩相互抵消，宏观上只表现出第三个Cu2+离子自旋的磁矩，导致磁化强度随磁场变化曲线在H=11~30 T 时出现一个1/3 平台。 随着磁场继续增大，相互抵消的磁矩被破坏掉，总磁矩迅速达到饱和。Kikuchi 等[63]测量了其高场磁化率和1H NMR， 发现该化合物的基态处于无能隙相。 此外，Kamikawa 等[64]通过高场电子顺磁共振测试发现该化合物在20 K 以下观察到朗德因子g 的位移，与磁化率曲线的变化一致。
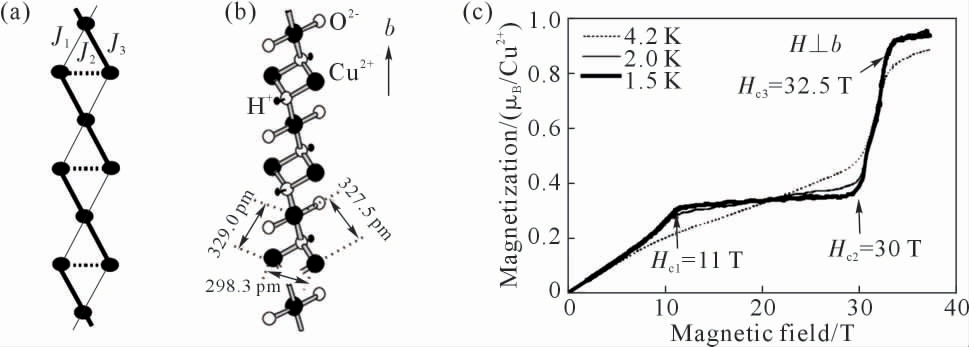
图6 Cu3(CO3)2(OH)2 的性质：(a)金刚石链结构，(b)晶体结构示意图，(c)高场磁化强度曲线[62]
Fig.6 The properties of Cu3(CO3)2(OH)2:(a)the diamond chain,(b)the crystal structure,(c)the high-field magnetization curves[62]
BaMn2V2O8 因具有大自旋的金属磁性离子Mn2+(S=5/2)，其基态磁性有可能表现出经典磁性行为与量子磁性行为并存的现象， 引起了科研工作者的极大兴趣[38]。 如图7(a)所示，BaMn2V2O8 结晶于四方晶系，Mn2+ 与6 个O 原子配位形成MnO6 八面体，Mn2+位于MnO6 八面体的中心。 MnOv 八面体通过共边的连接方式沿着c 轴延伸形成无限长的螺旋磁性链，链与链之间由碱土金属Ba2+和VO4 四面体隔开。磁化率随温度变化的曲线表明，BaMn2V2O8 的磁化率在170 K 左右形成了宽峰， 是低维磁性化合物的典型特征， 表明在该温度下化合物存在短程磁有序(图7(b))。 在37 K 时，磁化率随温度变化曲线出现典型的λ 型尖峰，表明BaMn2V2O8 出现了反铁磁性有序转变。Pal 等[65]通过温度依赖的拉曼光谱发现该化合物在奈尔温度以下至少存在2 种声子模式，在奈尔温度以上拉曼模式发生异常热演化，该现象与短程磁有序有关。
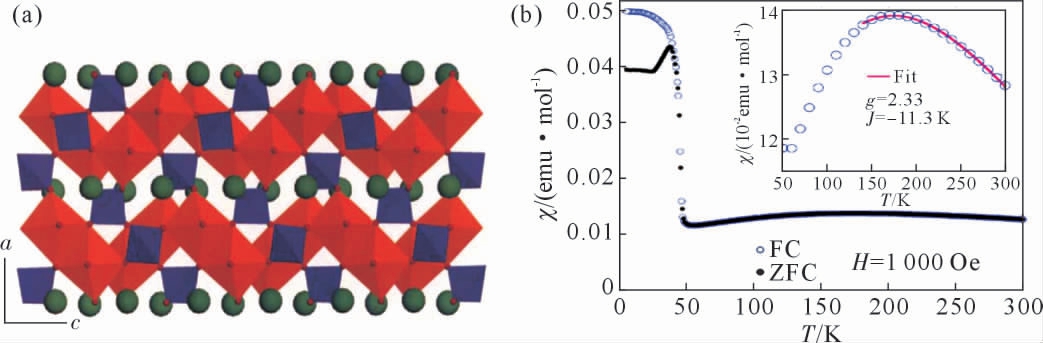
图7 BaMn2V2O8 的性质：(a)BaMn2V2O8 的晶体结构，(b)BaMn2V2O8 的磁化率随温度变化曲线[38]
Fig.7 The properties of BaMn2V2O8:(a)the crystal structure of BaMn2V2O8,(b)temperature dependence of magnetic susceptibility for BaMn2V2O8[38]
2 整数自旋一维量子反铁磁性材料
与具有半整数自旋的一维量子反铁磁性材料不同， 具有整数自旋的一维量子反铁磁性材料在其基态和激发态之间存在着有限能隙，该能隙又可以被称作为Haldane 能隙。 目前，该能隙在很多S=1 的化合物中被测得，如Ni(C3H8N2)2NO2ClO4(NENP)[66-68]，SrNi2V2O8[69-71]，RbNiCl3[72]，R2BaNiO5(R 为Y 或稀土元素)[73-74]。 研究较多的具有整数自旋的一维量子反铁磁性化合物主要包括NENP[66-68]、ANi2V2O8(A=Sr2+, Pb2+)[69-71]、MnCl3(2,2’-bpy)[75]等，依次简单介绍如下。
NENP 是首个被发现存在Haldane 能隙的化合物[68]。 该化合物的单晶样品是通过在水溶液中缓慢挥发得到[76]。 如图8(a)所示，Ni 原子在ac 平面内与2 个二甲胺的4 个N 原子配位。 在b 轴方向上，Ni原子通过亚硝酸根离子连接形成无限长的一维磁性链。 高氯酸根离子填充在链与链之间， 将磁性链隔开。 图8(b)表明，NENP 的磁化强度在低场时基本为0，当外加磁场增加至7.5 T 时，磁化强度开始呈直线上升，证实了Haldane 能隙的存在。
图8 NENP 的性质：(a)晶体结构，(b)磁化强度随磁场变化曲线[68]
Fig.8 The properties of NENP:(a)crystal structure,(b)field dependence of the magnetization[68]
PbNi2V2O8[7]是通过传统的固相合成方法制备得到，在室温时属于四方晶系，空间群为I41cd，晶胞参数为a=12.161 7 Å 和c=8.324 7 Å。 如图9(a)所示，PbNi2V2O8 中NiO6 八面体沿c 轴方向通过共边连接形成一维磁性链， 链与链之间通过VO4 四面体隔开，而Sr2+填充在金属链周围。磁化率随温度变化曲线表明该化合物在120 K 时出现一个宽峰， 随后磁化率迅速下降，在低温时随温度下降而上升，没有达到三维长程磁有序。 对磁化率进行分析可以得到热激活能Δ=29.4 K(H‖c)和Δ=27.8 K(H⊥c)。此外，图9(b)中磁化强度随磁场变化曲线的斜率发生了明显改变，表明存在磁相变，Haldane 能隙在临界场附近先闭合再打开。 Hashi 等[77]在30 T 时对该化合物进行了51V 核磁共振测试， 发现该化合物的核磁谱图在12 K 处开始分裂，表明在该温度时出现了反铁磁有序。
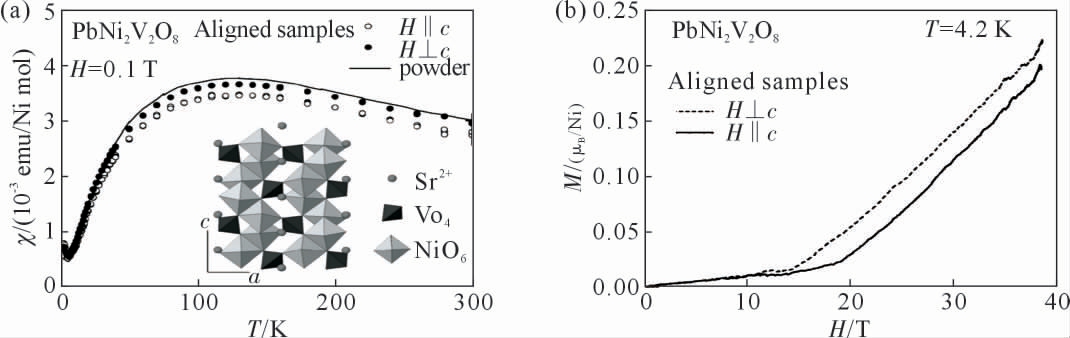
图9 PbNi2V2O8 的磁性能：(a)磁化率随温度变化曲线，(b)磁化强度随磁场变化曲线[7]
Fig.9 Magnetic properties of PbNi2V2O8:(a)temperature dependence of magnetic susceptibility,(b)field dependence of the magnetization[7]
Pahari 等 [69] 发现与PbNi2V2O8 结构相同的SrNi2V2O8 在温度低至3.75 K 时也未表现出长程磁有序， 与非弹性中子散射实验的结果相符合。 研究表明其Haldane 能隙约为25 K， 基态呈自旋液态，并进一步揭示了其在3.7~300.0 K 的温度范围内为反铁磁性相互作用。
自旋为S=2 的MnCl3(2,2-bpy)最初被认为是唯一一个在大自旋体系中实现Haldane gap 的化合物[75]，由常温挥发的方法制备得到[78]。 该化合物以Mn 为中心，与2,2’-bpy 的2 个N 原子和4 个Cl 原子配位形成MnN2Cl4 八面体。 MnN2Cl4 八面体以Cl原子作为桥联原子通过角连接的方式沿c 轴形成一维自旋链，链内∠Mn-Cl-Mn 为135°，表现出反铁磁性相互作用。 链与链之间通过有机分子2,2’-bpy和氢键相隔开， 使链间磁性金属Mn 的最近邻距离增大到7.96 Å，从而实现较弱的链间磁相互作用。如图10(b)所示，30 mK 下MnCl3(2,2-bpy)的磁化强度在低场时基本为0，直至H=1.2 T(H‖c)和H=1.8 T(H⊥c)时，磁化强度开始上升，表明该化合物存在Haldane 能隙[75]。
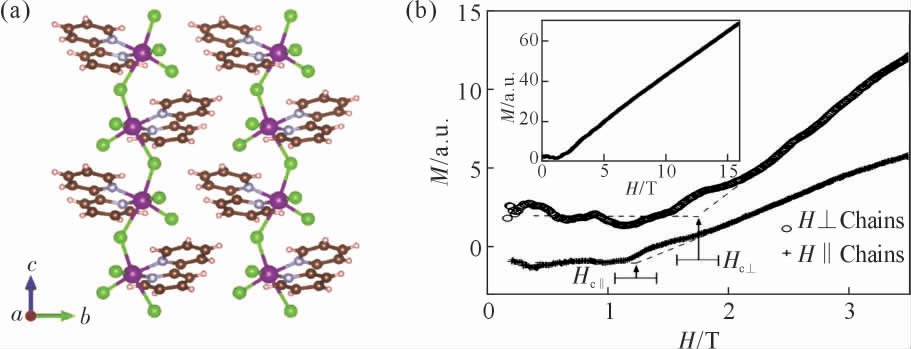
图10 MnCl3(2,2-bpy)的性质：(a)晶体结构，(b)磁化强度随磁场变化曲线[75]
Fig.10 The properties of MnCl3(2,2-bpy):(a)crystal structure,(b)field dependence of the magnetization[75]
然而在后续的研究中，Hagiwara 等[79]测量了MnCl3(2,2-bpy)单晶沿b 轴方向的磁化率随温度变化的曲线，结果显示化合物的磁化率在11 K 左右形成了尖锐的λ 型峰，表明MnCl3(2,2-bpy)在11 K 出现了反铁磁有序转变(图11)。
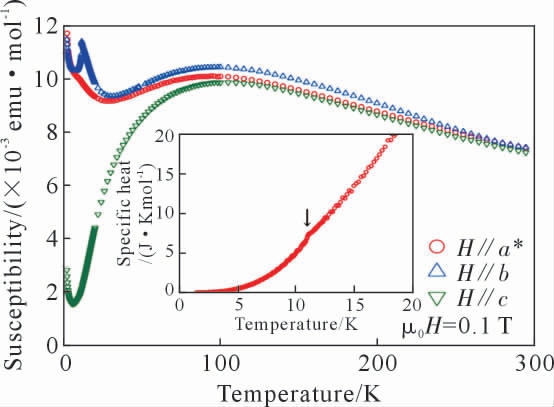
图11 MnCl3(2,2-bpy)沿a,b 和c 轴的磁化率随温度变化曲线[79]
Fig.11 Temperature dependence of magnetic susceptibilities for MnCl3(2,2-bpy)along the a,b and c axes[79]
3 总结和展望
目前， 通过各种实验方法合成得到的一维量子反铁磁性材料数量较多， 但可以表现出新奇磁性性能的一维量子反铁磁性材料较少。此外，在大自旋体系中能实现Haldane 能隙的化合物基本没有。因此，在今后对一维量子反铁磁性材料的研究中需要合成更多更优异的模型， 为人们进一步理解一维量子反铁磁性材料的本质、新奇量子现象的起源、超导现象的解释及后续的实际应用提供实验材料。
[1] BALENTS L.Spin liquids in frustrated magnets[J].Nature,2010,464:199-208.
[2] 冉柯静，王靖珲，温锦生.通往量子自旋液体的新路径——Kitaev 模型的材料实现[J]. 物理，2021,50(7):443-453.RAN K J,WANG J H,WEN J S.A new route to quantum spin liquids:Material realization of the Kitaev model[J].Physics,2021,50(7):443-453.
[3] DU L J, HUANG Y, WANG Y M, et al. 2D proximate quantum spin liquid state in atomic-thin α-RuCl3[J].2D Materials,2019,6(1):015014.
[4] LI Y S,CHEN G,TONG W,et al.Rare-earth triangular lattice spin liquid:A single-crystal study of YbMgGaO4[J].Physical Review Letters,2015,115:167203.
[5] HE Z Z, TANIYAMA T, KYÔMEN T, et al. Field-induced order-disorder transition in the quasi-one-dimensional anisotropic antiferromagnet BaCo2V2O8[J].PhysicalReviewB,2005,72:172403.
[6] MENTRE O,DHAUSSY A C,ABRAHAM F,et al.Structural,infrared, and magnetic characterization of the solid solution series Sr2-xPbx(VO)(VO4)2;evidence of the Pb2+6s2 lone pair stereochemical effect[J]. Journal of Solid State Chemistry,1998,140(2):417-427.
[7] UCHIYAMA Y, SASAGO Y, TSUKADA I, et al. Spin-vacancy-induced long-range order in a new haldane-gap antiferromagnet[J].Physical Review Letters, 1999, 83: 632-635.
[8] HASE M, TERASAKI I, UCHINOKURA K. Observation of the spin-Peierls transition in linear Cu2+(spin-1/2)chains in an inorganic compound CuGeO3[J].Physical Review Letters, 1993, 70(23):3651-3654.
[9] HASE M,TERASAKI I,UCHINOKURA K,et al.Magnetic phase diagram of the spin-Peierls cuprate CuGeO3[J].Physical Review B,1993,48:9616-9619.
[10] 卢蒙蒙， 陈斌. 含阻挫和各向异性的反铁磁自旋链的键算符理论[J].上海理工大学学报，2020,42(6):607-611.LU M M, CHEN B. Bond operator theory of antiferromagnetic spin chain with bond alternation and anisotropy[J].Journal of University of Shanghai for Science and Technology, 2020, 42(6):607-611.
[11] KUDO K, YAMAZAKI M, KAWAMATA T, et al. Drastic enhancement of thermal conductivity in the Bose-Einstein condensed state of TlCuCl3[J].Journal of the Physical Society of Japan,2004,73:2358-2361.
[12] NIKUNI T, OSHIKAWA M, OOSAWA A, et al. Bose-Einstein condensation of dilute magnons in TlCuCl3[J].Physical Review Letters,2000,84:5868-5871.
[13] RADU T, WILHELM H, YUSHANKHAI V, et al. Bose-Einstein condensation of magnons in Cs2CuCl4[J].Physical Review Letters,2005,95(12):127202.
[14] KAGEYAMA H, YOSHIMURA K, STERN R, et al. Exact dimer ground state and quantized mag netization plateaus in the two-dimemsional spin system SrCu2(BO3)2[J]. Physical Review Letters,1999,82:3168-3171.
[15] KIKUCHI H,FUJII Y,CHIBA M,et al.Experimental observation of the 1/3 magnetization plateau in the diamond-chain compound Cu3(CO3)2(OH)2[J].Physical Review Letters, 2005, 94: 227201.
[16] MATSUMOTO M. Microscopic model for the magnetization plateaus in NH4CuCl3[J].Physical Review B, 2003, 68,180403.
[17] CHEN R Y,WANG N L.Progress in Cr-and Mn-based superconductors:A key issues review[J].Reports on Progress in Physics,2019,82:012503.
[18] WANG D F, KONG L Y, FAN P, et al. Evidence for Majorana bound states in an iron-based superconductor[J]. Science, 2018,362(6412):333-335.
[19] KITAEV A. Anyons in an exactly solved model and beyond[J].Annals of Physics,2006,321(1):2-111.
[20] KITAEV A Y. Fault-tolerant quantum computation by anyons[J].Annals of Physics,2003,303(1):2-30.
[21] AHAMI N, BAZ M E. Thermal entanglement in a mixed spin Heisenberg XXX chain with DM interaction[J].International Journal of Quantum Information,2021,19(5):2150021.
[22] GNANA BLESSY B S, LATHA M M. Chaotic dynamics of Heisenberg ferromagnetic spin chain with bilinear and biquadratic interactions[J].Physica B:Condensed Matter,2017,523:114-124.
[23] GNANA BLESSY B S,LATHA M M.A chaotic study on Heisenberg ferromagnetic spin chain using Dzyaloshinski-Moriya interactions[J].Pramana,2019,93:70.
[24] GUARNACCIA G,NOCE C.Quantum disordered vector-spin-chirality stateinonedimensionalHeisenbergmodel[J].European Physical Journal B,2019,92:212.
[25] HANN C T, HUFFMAN E, CHANDRASEKHARAN S. Solution to the sign problem in a frustrated quantum impurity model[J].Annalsof Physics,2017,376:63-75.
[26] KRUPNITSKA O.Frustrated quantum Heisenberg double-tetrahedral and octahedral chains at high magnetic fields[J].Physical Review B,2020,102:064403.
[27] LI N B.Energy and spin diffusion in the one-dimensional classical Heisenberg spin chain at finite and infinite temperatures[J].Physical Review E, 2019, 100: 062104.
[28] POPKOV V,SCHÜTZ G M.Solution of the Lindblad equation for spin helix states[J].Physical Review E, 2017, 95: 042128.
[29] ROJAS O.A conjecture on the relationship between critical residual entropy and finite temperature pseudo-transitions of one-dimensional models[J].Brazilian Journal of Physics,2020,50:675-686.
[30] TORLAI G,MCALPINE K D,CHIARA G D.Schmidt gap in random spin chains[J].Physical Review B, 2018, 98: 085153.
[31] HALDANE F D M.Nonlinear field theory of large-spin Heisenberg antiferromagnets:Semiclassically quantized solitons of the one-dimensional easy-axis Néel state[J].Physical Review Letters,1983,50:1153-1156.
[32] 张广铭. 物理诺奖之Haldane 相的来龙去脉[J]. 物理，2016,45(12):769-773.ZHANG G M.The origin of the Haldane gapped phase[J].Physics,2016,45(12):769-773.
[33] BRAY J W,HART H R,INTERRANTE L V,et al.Observation of a spin-Peierls transition in a Heisenberg antiferromagnetic linear-chain system[J].Physical Review Letters,1975,35:744-747.
[34] INTERRANTE L V,BROWALL K W,HART H R,et al.Preparation and properties of some tetrathiafulvalene donor-acceptor compounds with bis (dithiolene) metal complexes[J]. Journal of the American Chemical Society,1975,97(4):889-890.
[35] JACOBS I S, BRAY J W, HART H R, et al. Spin-Peierls transitions in magnetic donor-acceptor compounds of tetrathiafulvalene(TTF)with bisdithiolene metal complexes[J].Physical Review B,1976,14:3036-3051.
[36] HASE M,TERASAKI I,SASAGO Y,et al.Effects of substitution of Zn for Cu in the spin-Peierls cuprate,CuGeO3:The suppression of the spin-Peierls transition and the occurrence of a new spin-glass state[J].Physical Review Letters,1993,71:4059-4062.
[37] TSUKADA I,TAKEYA J,MASUDA T,et al.Two-stage spin-flop transitions in the S=1/2 antiferromagnetic spin chain BaCu2Si2O7[J].PhysicalReviewLetters,2001,87:127203.
[38] HE Z Z, UEDA Y, ITOH M. Magnetic properties of the quasi-one-dimensional system BaMn2V2O8[J].Solid State Communication,2007,141(1):22-24.
[39] LÉPINE Y, CAILL É A. First order spin-Peierls transition in a quantum antiferromagnetic Heisenberg chain[J].The Journal of ChemicalPhysics,1977,67(12):5598-5601.
[40] CHEN Y, SATO M, TANG Y F, et al. Triplon current generation in solids[J].Nature Communications,2021,12:5199.
[41] PARIS E,NICHOLSON C W,JOHNSTON S,et al.Probing the interplay between lattice dynamics and short-range magnetic correlations in CuGeO3 with femtosecond RIXS[J].npj Quantum Materials,2021,6:51.
[42] SUZUKI V Y, AMORIN L H C, DE PAULA N H, et al. New insights into the nature of the bandgap of CuGeO3 nanofibers: Synthesis, electronic structure, and optical and photocatalytic properties[J].Materials Today Communications, 2021,26:101701.
[43] XIAO Y M,LI B,QIN L Z,et al.Efficient preparation of CuGeO3 with controllable morphology using CuCl2 as copper source[J].Journal of Inorganic Materials,2021,36(1):69-74.
[44] XU H Z, ZHANG S Y, GUO G C, et al. Exact dimer phase with anisotropic interaction for one dimensional magnets[J].Scientific Reports,2021,11:6462.
[45] VÖLLENKLE H, WITTMANN A, NOWOTNY H. Zur kristallstruktur von CuGeO3[J].Monatshefte für Chemie und Verwandte Teile anderer Wissenschaften, 1967,98:1352-1357.
[46] HIROTA K,COX D E,LORENZO J E,et al.Dimerization of Cu-GeO3 in the spin-Peierls state[J].Physical Review Letters, 1994,73:736.
[47] HAMAMOTO T, ADACHI N, KIDO G, et al. Phase diagram of spin-Peierls cuprate CuGeO3 based on ac susceptibility in high magnetic fields[J].Journal of the Physical Society of Japan,1994,63:1218-1219.
[48] HORI H, FURUSAWA M, TAKEUCHI T, et al. Magnetic measurements of CuGeO3 by means of high magnetic field [J].Journal of the Physical Society of Japan,1994,63(1):18-21.
[49] KIKUCHI J,YASUOKA H,HASE M,et al.Cu nuclear quadrupole resonance study of CuGeO3[J].Journal of the Physical Society of Japan,1994,63(3):872-875.
[50] KUROE H,KOBAYASHI K,SEKINE T,et al.Heat capacity in an Inorganic spin-Peierls system CuGeO3 [J].Journal of the Physical Society of Japan,1994,63(1):365-366.
[51] HASE M, TERASAKI I, UCHINOKURA K. Observation of the spin-Peierls transition in linear Cu2+ (spin-1/2) chains in an inorganic compound CuGeO3[J]. Physical Review Letters, 1993,70(23):3651-3654.
[52] SUGA S. Two-magnon raman scattering in CuGeO3 which undergoes spin-Peierls transition[J]. Journal of the Physical Society of Japan,1993,62(11):3829-3831.
[53] LI Z Q, ZHANG L, SONG Y, et al. Size-controlled synthesis and magnetic properties of copper germanate nanorods.Observation of size-induced quenching of the spin-Peierls transition[J].CrystEng-Comm,2014,16(5):850-857.
[54] TSUKADA I, SASAGO Y, UCHINOKURA K, et al. BaCu2Si2O7:A quasi-one-dimensional S=1/2 antiferromagnetic chain system[J].Physical Review B,1999,60(9):6601-6607.
[55] LEE P L,HUANG E,KUNG J.High-pressure raman spectroscopy and X-ray diffraction study on scottyite, BaCu2Si2O7[J].Minerals,2021,11(6):608.
[56] RENDÓN-ANGELES J C,QUIÑONES-GURROLA J R,LÓPEZCUEVAS J,et al.Rapid one-pot hydrothermal reaction for preparing BaCu2Si2O7 fine particles with controlled blue colour tonality[J].Ceramics International,2021,47(7):9354-9365.
[57] SHIROKA T,EGGENSCHWILER F,OTT H R,et al.From order to randomness: Onset and evolution of the random-singlet state in bond-disordered BaCu2(Si1-xGex)2O7 spin-chain compounds[J].Physical Review B,2019,99:035116.
[58] SONG X Q,LU W Z,LOU Y H,et al.Synthesis,lattice energy and microwave dielectric properties of BaCu2-xCoxSi2O7 ceramics[J].Journal of the European Ceramic Society,2020,40(8):3035-3041.
[59] SONG X Q,ZOU Z Y,LU W Z,et al.Crystal structure,lattice energy and microwave dielectric properties of melilite-type Ba1-xSrx-Cu2Si2O7 solidsolutions[J].Journal of Alloys and Compounds,2020,835:155340.
[60] WANG G H,XU C Y,CAO H B,et al.Magnetic properties of the low-dimensional BaM2Si2O7 system (M=Cu,Co,Mn)[J]. Physical Review B,2019,100:035131.
[61] ZHANG Z G,MA Q L,BERKE H.Man-made blue and purple barium copper silicate pigments and the pabstite(BaSnSi3O9)mystery of ancient chinese wall paintings from luoyang[J]. Heritage Science,2019,7:97.
[62] KIKUCHI H,FUJII Y,CHIBA M,et al.Experiment observation of the 1/3 magnetization plateau in the diamond-chain compound Cu3(CO3)2(OH)2[J].Physical Review Letters,2005,94:227201.
[63] KIKUCHI H,FUJII Y,CHIBA M,et al.Magnetic properties of the frustrated diamond chain compound Cu3(CO3)2(OH)2[J].Physica B:Condensed Matter,2003,329-333:967-968.
[64] KAMIKAWA T,OKUBO S,KUNIMOTO T,et al.High field ESR measurement of diamond chain substance Cu3(OH)2(CO3)2[J].Physica B:Condensed Matter, 2003, 329-333: 988-989.
[65] PAL A, ANAND K,YEN T W, et al. Magnetic properties and coulped spin-phononbehaviorinquasi-one-dimensionalscrew-chain compound BaMn2V2O8[J]. Physical Review Materials, 2023,7:014402.
[66] KATSUMATA K, HORI H, TAKEUCHI T, et al. Magnetization process of an S=1 linear-chain Heisenberg antiferromagnet [J].Physical Review Letters,1989,63:86-88.
[67] LU W,TUCHENDLER J,VON ORTENDERG M,et al.Direct observation of the Haldane gap in NENP by far-infrared spectroscopy in high magnetic fields[J]. Physical Review Letters, 1991, 67:3716-3719.
[68] REGNAULT L P, ZALIZNYAK I, RENARD J P, et al. Inelastic-neutron-scattering study of the spin dynamics in the Haldane-gap system Ni(C2H8N2)2NO2ClO4[J].Physical Review B,1994,50:9174-9187.
[69] PAHARI B,GHOSHRAY K,SARKAR R,et al.NMR study of 51V in quasi-one-dimensional integer spin chain compound SrNi2V2O8[J].Physical Review B,2006,73:012407.
[70] GNEZDILOV V,KURNOSOV V,PASHKEVICH Y,et al.Non-Abelian statistics in light-scattering processes across interacting Haldane chains[J].Physical Review B, 2021,104:165118.
[71] KURNOSOV V,GNEZDILOV V,LEMMENS P,et al.Phonon excitations in the quasi-one-dimensional Haldane phase of SrNi2V2O8[J].Low Temperature Physics,2017,43(12):1405-1414.
[72] TUN Z,BUYERS W J L,HARRISON A,et al.Observation of the Haldane gap in RbNiCl3[J].Physical Review B,1991,43:13331.
[73] DARRIET J, REGNAULT L P. The compound Y2BaNiO5: A new example of a haldane gap in a S=1 magnetic chain[J].Solid State Communications,1993,86(7):409-412.
[74] MASLOV S, ZHELUDEV A. Coexistence of Haldane-gap excitations and long-range antiferromagnetic order in mixed-spin nickelates R2BaNiO5[J].Physical Review B,1998,57:68-71.
[75] GRANROTH G E,MEISEL M W,CHAPARALA M,et al.Experimental evidence of a Haldane gap in an S=2 quasi-linear-chain antiferromagnet[J].Physical Review Letters, 1996, 77: 1616-1619.
[76] YOSIDA T, FUKUI M. Crystal structure of Ni(C3H10N2)2NO2ClO4[J].Journal of the Physical Society of Japan,1992,61:2304-2308.
[77] HASHI K, TSUJII N, SHIMIZU T, et al. NMR evidence for field-induced magnetic ordering at 30 T in the Haldane compound PbNi2V2O8[J].Journal of the Physical Society of Japan, 2007,76:064705.
[78] PERLEPES S P, BLACKMAN A G, HUFFMAN J C, et al. Complete carboxylate removal from Mn12O12(OAc)16(H2O)4·2HOAc·4H2O with chlorotrimethylsilane: Synthesis a and characterization of polymeric(2,2'-bipyridine)trichloromanganese and an improved synthesis of bis (tetraethylammonium) pentachloromanganate(2-)[J].Inorganic Chemistry, 1991,30(7):1665-1668.
[79] SHINOZAKI S, OKUTANI A, YOSHIZAWA D, et al. Antiferromagnetic order in single crystals of the S=2 quasi-one-dimensional chain MnCl3(bpy)[J].Physical Review B,2016,93:014407.