STL 模型是目前增材制造工艺中最常使用的标准文件类型, 其中包含大量三角面片的数据信息,包括3 个顶点的坐标数据及三角面片所在平面的法向量坐标,将所有三角面片在三维空间中链接便可得到一个完整的三维图形[1-5]。 STL 模型切片是增材制造中的关键环节,相关算法直接决定模型制作的效率与准确性。 目前广泛使用的STL 模型切片方法均在最基础的直接切片方法上做了一定程度的优化[6-9],其算法基础是将切平面与三角面片的交点按照拓扑结构连接成闭合轮廓。
当切面存在轮廓相交现象时, 若不对此奇异情况进行特殊处理,直接进行轮廓顶点排序,可能出现错误情况。 造成此类奇异情况的主要原因是切平面与待切模型的某一边重合或相切。针对此类问题,目前常用的方法是顶点转移法, 该方法将与切平面重合的点、边、面沿层切方向向上或向下平移微小距离来避免奇异问题[10],但是这种改变模型顶点位置的方法会对模型精度造成一定影响。 吴建等[11]提出了一种避免轮廓相交的STL 模型快速切片方法,其采用基于图和Delaunay 三角剖分结合的方法对相交轮廓进行修复,关键在于使用三角剖分时需要持续对图的外部边界进行判断,逻辑较为复杂,运算及判断次数较多,运算时间复杂度较高。
对于某些较为复杂或者包含孔洞的STL 模型,难度在于某层切片可能出现相互不连通的多个闭合路径[12]。 单一深度优先算法只能实现无向图中一个闭合路径的遍历, 且无法对轮廓进行闭合处理,因此需要对相关算法进行改进。 针对以上2 个难点,本文提出一种优化算法,特别提出将射线法与深度优先搜索结合解决轮廓相交问题的方法,并使用多重深度优先搜索算法对包含多个不连通闭合路径的轮廓进行拓扑。
1 算法实现
1.1 三角面片分层求交
切片算法的第一步需要处理STL 模型中混乱的三角面片数据,以提高切片效率。
将每一个三角面片的3 个顶点按照切片方向高度进行排序(本文以垂直于Z 方向为切片方向),ZA>ZB>ZC。 通过ZC 与切面高度的关系对所有三角面片进行分层: 由低到高, 第n 层切面高度为Zn,将Zn≥ZC>Zn-1 的三角面片归属于第n 层,若ZA 与ZC 同时处于(Zn, Zn+1)区间内,则该三角面片与切面无交点,不加入任一层三角面片集合。 由于一个三角面片可能跨越多层切面高度,所以在使用第n 层三角面片数据时,需要对第(n-1)层三角面片部分数据进行继承[13]。如图1 所示,以下4 个三角面片均属于第(n-1)层,但其中的2、4 三角面片与第n 层切面仍存在有效交点,故使用第n 层三角面片数据时需要从第(n-1)层三角面片中继承2、4 三角面片的数据。 以上这种分层方法在调用第n 层数据时仅需要对第(n-1)层数据进行遍历判断和继承而无需遍历所有三角面片,提升了工作效率并减少了内存占用。
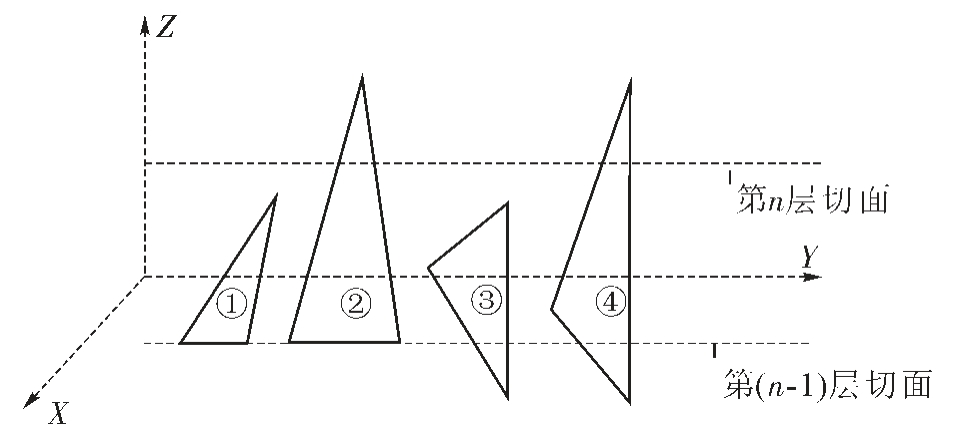
图1 三角面片分层示意图
Fig.1 Schematic diagram of triangular patch layering
根据上述分层方法, 每层的三角面片可分为以下几类,如图2 所示。
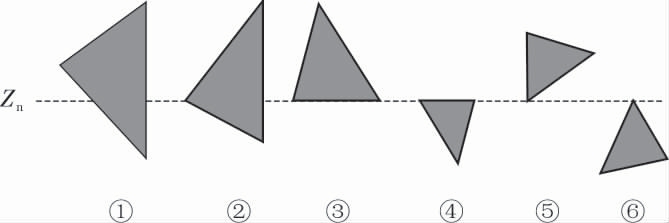
图2 三角面片与切面交点图
Fig.2 Diagram of intersection of triangular patch and cut plane
(1)ZC
(2)ZC
(3)Zn=ZA=ZB 或者Zn=ZB=ZC,如图2③④,三角面片的两个交点为与切面高度相同的两个顶点。
(4)ZA=Zn 或ZC=Zn,且ZB≠Zn,如图2⑤⑥,此类三角面片与切面无有效交点。
1.2 优化相交轮廓
一个常规的STL 模型切片轮廓应该包括不含相交线段的一个或多个闭合路径, 但切片过程中切面恰好与模型的某一边或面重合或相切时, 可能出现轮廓相交的奇异问题[11]。 如图3(a)所示,切平面与曲轴各部件连接线相重合,切面轮廓拓扑如图3(b),各个部件之间出现了轮廓相交的奇异现象, 而增材制造中所需的切片轮廓如图3(c)所示。 故需要对算法进行优化以便在出现上述现象时获取最外围的有效轮廓,提高切片的准确率。 为便于描述,下文将图3(b)中各个轮廓之间的交点称作奇异交点。

图3 轮廓相交奇异现象示例图
Fig.3 Singular phenomenon of contour intersection
1.2.1 获取轮廓相交产生的交点
根据上述分层求交的方法, 可求得层面交点集合V’={V1,V2,V3,...Vn},从起点开始,每2 个连续交点为一个三角面片与切面的交点线段, 建立交点线段集合E={
通过邻接矩阵,判断每一个顶点在轮廓中的邻点个数。 在一个无分支的闭合轮廓中,每一个顶点的邻点个数均为2。 若邻点个数大于2,则此顶点为一个由轮廓相交产生的交点,将其索引号存入奇异交点集合S。
1.2.2 获取最外围轮廓
轮廓相交会使一个切片拓扑结构中出现多个相交的闭合路径,但其中只有一个闭合路径为所需的有效轮廓,即最外围路径。 据奇异交点的特点可知,奇异交点总是最外围路径与其余冗余路径的交点。 因此,以奇异交点集合S 中的一个元素为起点,基于邻接矩阵A 通过深度优先搜索算法求出图中经过S 全部元素的所有闭合路径的集合P, 则集合P 中的某一元素必定是最外围路径。 深度优先搜索(depth-first search,DFS) 算法从图G 的初始节点开始向图的更深处搜索,直至找到目标节点或没有子节点的节点[14-15]。具体步骤:以奇异交点集合S 中一个元素为起点P1,搜索与其相邻且未被访问过的顶点P2, 再以P2 为起点搜索与其相邻且未被访问过的顶点P3,……,以此迭代,直至当前访问的顶点的所有邻点均被访问且其邻点之一为起点P1,构成一条闭合路径P1-P2-P3-...-P1。
以图4 为例,奇异交点集合S=<1,2,3,4>,可得图4中经过所有奇异交点的路径为P={(1,2,3,4,6,1),(1,2,3,4,5,1),(1,2,7,3,4,6,1),(1,2,7,3,4,5,1)}。
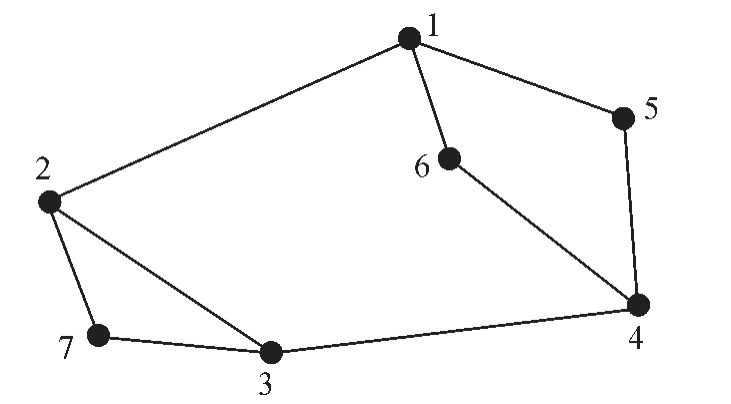
图4 轮廓相交切片拓扑示例图
Fig.4 Topology of slice with intersecting contours
求取经过所有奇异交点的闭合路径后,需要找出最外围的闭合路径。 利用射线法对当前闭合路径与不在此路径上的其余顶点的位置关系进行判断。射线法通过由点发出的射线与闭合路径的交点个数的奇偶性判断点和闭合路径的位置关系[16]。 针对集合V 中所有元素建立一个Status 数组,每个顶点的初始状态均为“0”,若为“1”则表示此元素对应的点处于某个闭合路径之内, 即以此点为某一顶点的所有闭合路径不可能是所求的最外围路径。 取集合P 中一个元素Pi,以集合V 中不在Pi 上的元素Vi 为顶点作射线,若射线与Pi 的交点个数为奇数,则代表Vi 处于Pi 路径包含的范围之内, 将Vi 在数组Status 中对应的元素更改为“1”,此点不可能是最外围路径的顶点。 取下一个不在Pi 上且Status 数组中对应元素为0 的顶点Vj 重复上述位置判断,若射线与Pi 的交点个数为偶数, 则代表Vi 处于Pi 路径包含的范围之外,则Pi 不可能为最外围路径,终止对此路径的判断。选取下一个不包含状态为“1”的顶点的路径重复上述判断。 直至某一路径与所有不在其路径上的顶点所作射线的交点个数均为奇数, 此路径为最外围路径。
仍以图4 为例,顶点集合V={1,2,3,4,5,6,7},Status 数组为[0,0,0,0,0,0,0]。 具体步骤如下:
(1)如图5 所示,选取集合P 中元素P3={1,2,7,3,4,6,1}为第一个分析的路径,以5 为顶点作射线,与P3 的交点个数为0(右向射线)或2(左向射线),则P3不是最外围路径。
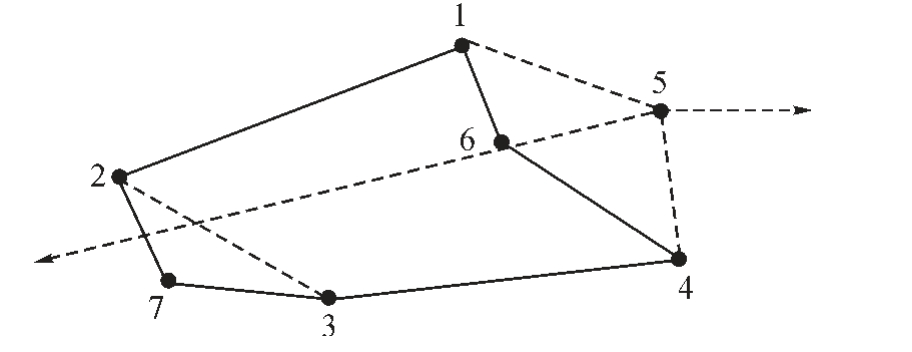
图5 射线法示意图
Fig.5 Topology of slice with intersecting contours using ray-casting
(2)选取P2={1,2,3,4,5,1}为第二个分析的路径,以6 为顶点作射线, 与P2 的交点个数为奇数, 即6非最外围路径的顶点, 此时Status 数组更新为[0,0,0,0,0,1]。
(3)以7 为顶点作射线,与P2 的交点个数为0 或2,即P2 也不是最外围路径。
(4)选取不包含Status 数组对应元素为“1”的顶点的路径P4={1,2,7,3,4,5,1}为第三个分析的路径,以6 为顶点所作的射线与P2 的交点个数为1, 得出P4为最外围路径。
(5)更新集合V,将V 中非最外围轮廓的顶点元素删除。
需要特别说明的是: 若一对奇异交点直接构成原始切面拓扑的一条边, 存在所有顶点同时在一个闭合路径上的情况, 没有其余点作为射线顶点来对点与闭合路径的相对位置关系进行判断, 因此需取奇异交点所构成的边上一点作为一个新增的顶点,同样按照上述方法求最外围轮廓。 如图6 所示,<1,3>为奇异交点构成的边,点P 为新增顶点。
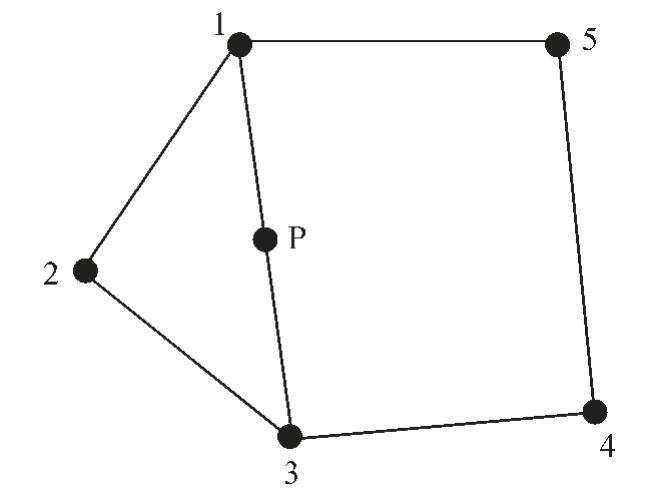
图6 奇异交点的特殊情况
Fig.6 Special cases of singular intersections
1.3 多重深度优先搜索对层面顶点排序
经过上述方法的处理,可保证集合V 中元素可拓扑为只包含相互不连通的闭合路径的切面轮廓,即每个顶点的邻点个数均为2。 对于包含孔洞的复杂STL 模型,其切片拓扑可能包含多个相互不连通的闭合路径,因此使用多重深度优先搜索对所有闭合路径的顶点进行排序。
针对顶点集合V 中所有元素建立一个Visited数组,数组中每个元素表示集合V 中对应顶点的访问状态,初始状态均为“0”。重建邻接矩阵,以集合V中某一点为起点进行深度优先遍历,将每次遍历的点对应的Visited 元素设为“1”,表示已访问。 再将每次遍历到的点存入集合Path 中,检测当前访问点的邻点,若两个邻点均为已访问状态且其中一个邻点为起点,则表示当前轮廓已完成遍历,主动向集合Path 尾部添加起点坐标,实现轮廓闭合。 以上操作仅完成了一个闭合路径的顶点排序,在切片存在多个不连通闭合轮廓的情况下,仍需要对Visited 数组元素进行遍历,若存在未被访问的点,即代表图中存在其他闭合轮廓,以其中一点为起点,重复上述操作,直至Visited 数组中所有元素均为“1”,最终完成所有闭合轮廓顶点排序。
2 实例验证
利用Qt 开发平台编写测试代码,调用OpenGL对模型进行三维显示[17-18],并使用QCustomPlot 对切面轮廓进行显示[19-20]。
首先选用一机械零件(图7)进行测试。此模型为流行STL 数据测试模型,包含多个孔洞,且其表面存在大量与切面方向平行的三角面片。 对此STL 模型进行切片处理, 其结果能充分表现上述算法解决轮廓相交问题和实现多空洞复杂STL 模型切面拓扑的能力。

图7 零件测试用例原型
Fig.7 Image of part model test case
如图8(a)所示,当切平面和零件上半部与下半部的连接线重合时, 模型与切平面的交点拓扑图如图8(b)所示。显然,由于切平面与模型的边缘线段重合,切片过程中出现了轮廓相交的奇异现象。若直接对所有交点进行排序构造切片图形, 在奇异交点处有多条分支路径可以选择,无法判断轮廓分支走向,导致切片出错,无法形成无分支的闭合轮廓,测试结果如图8(c)所示。 经本文所述算法对相交轮廓进行处理后,测试效果如图8(d)所示,实验结果表明,此算法能较好的解决轮廓相交的奇异问题, 获取有效的外围闭合路径,同时实现了对于零件下半部的多个孔洞轮廓拓扑。
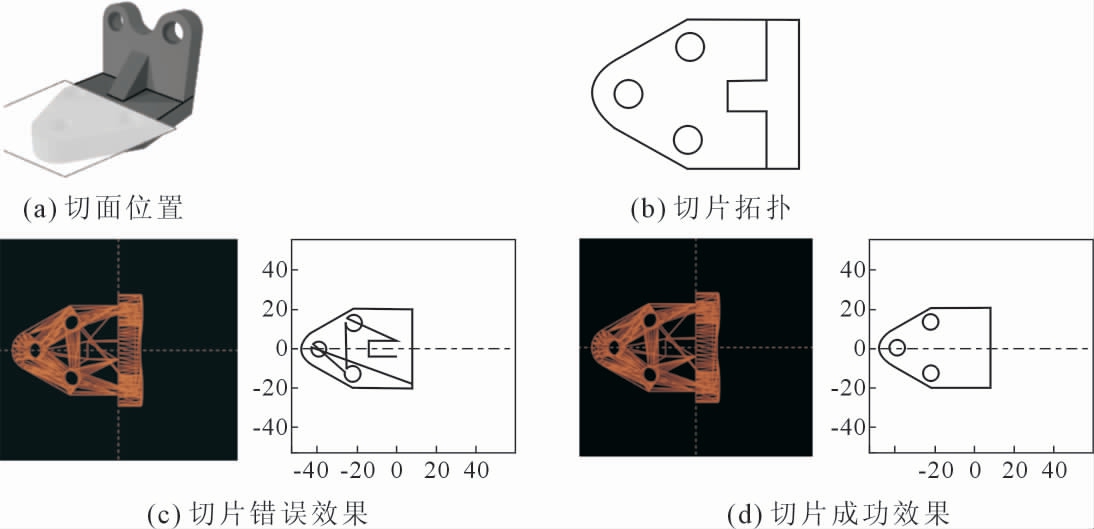
图8 零件切片测试图
Fig.8 Images of the part slicing test
选用某复杂昆虫模型作为测试用例,原型实例如图9 所示。 此模型由多个昆虫足部部件、昆虫头部部件和昆虫尾部部件拼接而成,平行于此模型背部方向进行切片,其切片拓扑图形中将存在大量的独立闭合路径。 观测此模型的切片拓扑结果可验证本文所述算法的可靠性。

图9 昆虫模型测试用例原型
Fig.9 Image of insect model test case
切片效果如图10 所示,实验结果表明,对于切面轮廓包含多个闭合路径的复杂STL 模型,此算法能对各个独立闭合路径顶点进行排序,从而实现整个复杂切片轮廓的拓扑。
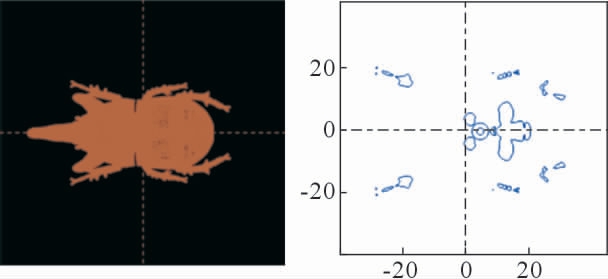
图10 昆虫模型测试效果图
Fig.10 Image of insect model test result
为了验证本文所述算法在切片效率上的优越性,与基于STL 模型中三角面片邻接关系的传统切片算法进行比较。 设模型与某层切面存在有效交点的三角面片的个数为m: 传统切片算法通过三角面片与切平面交点构成的交点线段的连通关系,将所有三角面片与切平面的交点排序并连接成闭合轮廓, 每次在获取下一个顶点坐标时都需要遍历剩余的所有交点线段的顶点坐标以找到邻接的交点线段,有效交点个数为(2m),因此其时间复杂度为O((2m)2)。
若使用基于邻接矩阵的深度优先搜索算法,忽略奇异情况对顶点个数的影响,由于所有的交点线段首尾相接,去除重复顶点后,邻接矩阵中节点个数可近似视为((2m)/2),因此其时间复杂度为O(m2)。
同样使用图9 所示昆虫模型进行测试,总切片层数为72 层。 为避免切片轮廓图像渲染时间影响实验数据, 将三角面片分层求交完成时刻作为开始时刻,将轮廓顶点排序完成时刻作为结束时刻。本文所述算法平均单层处理时间为69 ms, 传统切片算法平均单层处理时间为212 ms,由于本文所述算法中还包括对轮廓相交奇异现象的检测过程, 因此实验结果近似满足两种算法理论上的时间复杂度的差异。 而后使用多个流行STL 测试模型进行实验,本文所述算法单层处理时间稳定保持在传统切片算法的32%~38%之间。
3 结论
本文针对STL 模型在切片过程中出现的轮廓相交奇异问题, 提出了一种将射线法与深度优先搜索相结合的优化算法, 并利用多重深度优先搜索算法对包含孔洞的复杂STL 模型进行切片拓扑。
由实验结果得出以下结论:
(1)本文提出的优化算法能准确地在存在相交轮廓的切片拓扑中获取最外围有效轮廓, 解决切片过程中轮廓相交的奇异问题;
(2)对于复杂STL 模型,此算法能很好地完成包含多闭合路径的切片拓扑工作;
(3)使用基于图论的深度优先搜索算法获取所有闭合路径,避免对STL 模型中三角面片邻接关系进行重构,尤其是在对较为复杂的STL 模型进行切片时,可以大大减少时间成本,对于提高增材制造过程中的切片效率具有重要意义。
[1]许德,高华兵,董涛,等.增材制造用金属粉末研究进展[J].中国有色金属学报,2021,31(2):245-257.
[2]樊自田,杨力,唐世艳.增材制造技术在铸造中的应用[J].铸造,2022,71(1):1-16.
[3]卢秉恒.增材制造技术——现状与未来[J].中国机械工程,2020,31(1):19-23.
[4]朱虎,杨忠凤,张伟.STL文件的应用与研究进展[J].机床与液压,2009,37(6):186-189.
[5]文豪,高健,张正甫.面向STL文件的截面轮廓线段连接方法研究[J].机械设计与制造,2021,365(7):171-175.
[6]钱乘,李震,江本赤.基于冗余信息的STL模型快速切片算法[J].制造技术与机床,2018(4):69-74.
[7]吴建,吴婷,陈廷豪,等.基于MATLAB 的STL 模型切片分层算法[J].科技创新与应用,2020(2):23-24.
[8]王素,刘恒,朱心雄.STL 模型的分层邻接排序快速切片算法[J].计算机辅助设计与图形学学报,2011,23(4):600-606.
[9]田仁强,张义飞.快速成型中STL 模型直接切片新算法研究[J].机床与液压,2019,47(16):55-59.
[10]KIM H J,WIE K H,AHN S H,et al.Slicing algorithm for polyhedral models based on vertex shifting[J].Korean Society for Preci-sion Engineering,2010,11(5):803-807.
[11]吴建,吴婷,陈廷豪,等.一种避免轮廓相交的STL 模型快速切片方法[J].制造技术与机床,2021(12):91-95.
[12]马永壮,刘伟军,董遇泰.基于有向加权图递归切片算法的研究[J].中国机械工程,2003(14):1221-1223.
[13]赵吉宾, 刘伟军.快速成形技术中基于STL 模型的分层算法研究[J].应用基础与工程科学学报,2008,16(2):224-233.
[14]王远敏.深度优先搜索算法的应用研究[J].网络安全技术与应用,2022(3):40-42.
[15]嘉兴学院.一种基于图论的3D 打印切片处理方法[P].中国专利,201910742360.1,2019-11-12.
[16]苗春葆.点与多边形关系的射线法[J].电脑编程技巧与维护,2008(3):56-58.
[17]庄云良,赵东标,刘凯,等.基于VC 和OpenGL 的STL 文件的分层和显示[J].机械与电子,2012(1):27-30.
[18]耿铁, 任清海.基于OpenGL 的STL 文件三维模型真实感图形视化研究[J].制造业自动化,2011,33(16):121-124.
[19]徐瑶.Qt 中基于QCustomPlot 实现曲线绘制和显示的研究[J].科技视界,2019(25):54-55.
[20]钟权,沈静波,路伟欣.基于QCustomPlot 和Qt 的曲线绘制及显示技术[J].科技视界,2017(6):46-47.