采用数值计算方法能够解决铸造中无法解决的复杂问题,与实验相比,所需的费用和时间较少,而且精度较高,被广泛应用。 由于数值模拟技术能够预测铸造缺陷, 从而催生了多种铸造模拟软件,并应用于铸造领域,指导铸造工艺设计,如使用Pro-CAST 软件对铸造过程进行模拟[1-4]。 此外,针对具体铸造问题,还可以通过对模拟软件进行二次开发或自编程序进行模拟分析。 涂武涛等[5]利用宏观偏析数学模型, 分别对53 t 钢锭和500 t 铸件宏观偏析进行数值模拟研究。 冀焕明等[6]采用有限元方法对AZ80 镁合金低压脉冲磁场半连续铸造过程的电磁场、流场和温度场进行数值模拟,对铸锭的组织进行观察和分析, 并与普通半连续铸造铸锭晶粒组织进行对比。凌云等[7]通过铸造CAE 软件能够准确地预测钛合金铸件可能产生的气孔、缩松缩孔等缺陷。郭钊等[8]改进有限差分网格,对高温合金叶片定向凝固传热过程进行数值模拟,并采用不同的工艺参数进行对比分析。许庆彦等[9]介绍了高温合金定向凝固多尺度数值模拟方法,包括宏观温度场模拟方法、介观晶粒组织模拟方法与微观枝晶组织模拟方法等。王欢等[10]利用三维可视化离心铸造数值模拟技术模拟某钛合金薄壁件的充型凝固过程, 预测缺陷可能的位置。邵珩等[11]针对Ti-6Al-4V 合金熔模铸造固态相变过程中的微观组织演变,采用了多组元Zener-Hillert模型计算α 相片层边缘生长速率。
多数商用铸造模拟软件用户权限受限, 只能通过设定初始条件、边界条件,以及调整网格尺寸、时间步长等对铸造过程进行模拟分析, 难以对核心控制方程修改或选择。 因此,本文基于Microsoft Excel,采用简易的VBA 程序进行凝固模拟开发, 通过控制方程及算法,研究凝固潜热释放对任意简单铸件截面进行铸造模拟,以及考虑铸件与铸型之间的涂料对铸造凝固的影响,并对铸造过程进行模拟分析。
1 模拟方法
1.1 导热微分方程的一般形式:

式中,T 为温度,K;t 为时间,s;λ 为热导率,W/ (m·K);ρ 为密度,kg/m3;c 为比热容,J/(kg·K);Q˙为单位体积内热源的热能,J。
1.2 初始条件及边界条件
采用第三类边界条件,规定边界上物体与周围流体间的表面传热系数α 及周围流体的温度Tf。 以物体被冷却的场合为例,第三类边界条件表示为:
式中,Tw 为规定边界温度,K;Tf 为周围流体的温度,K。
1.3 铸件传热
在导热中,将平壁导热的计算公式改写为:
式中,热流密度q 为导热过程的转移量,温差ΔT 为导热过程的动力,而δ/λ 则为导热过程的阻力(δ 为单层平壁的壁厚)。在由两种材料组成的复合导热系统中, 如热导率分别为λ1 和λ2 的两种不同材料组成一种简单的复合平板,热量的传递有可能变得复杂起来, 这与两种界面处的接触情况有很大关系,在理想接触的情况下,可以利用热阻的概念来分析复合平板的导热问题[12]。 本程序中网格m 与网格n之间的传热[13]如图1 所示。

图1 内部网格传热示意图
Fig.1 Schematic of heat transfer between internal grids
由网格n 向网格m 传输的热量:
式中,Tm 为网格m 的温度,K;Tn 为网格n 的温度,K;Rns 为网格n 中心到网格边界之间的热阻,K/W;Rsm为网格边界到网格m 中心之间的热阻,K/W。 其中:
式中,Δx 为每个网格的宽度,m;Δy 为是每个网格的高度,m;λn 为网格n 的导热系数,W/(m·K);λm 为网格m 的导热系数,W/(m·K)。 则网格j 与网格i 之间的总热阻:
令![]() ),则
),则
1.4 铸件-铸型边界传热
边界条件为第三类边界条件, 在此类边界条件下网格与环境之间的传热如图2 所示。
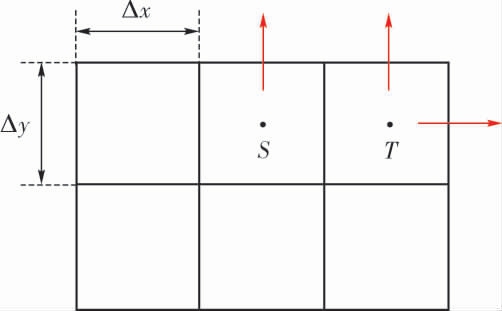
图2 铸件-铸型边界传热示意图
Fig.2 Schematic of heat transfer between internal and external grids
网格S 向环境传输的能量为:
式中,Ts 为网格S 的温度,K;To 为环境的温度,K;Rsb 为网格S 中心与边界之间的热阻,K/W;Rbo 为边界与环境之间的热阻,K/W。 其中,
式中,λs 为网格S 的导热系数,W/(m·K);α 为铸件与空气间的表面传热系数,W/(m2·K)。
令![]() ,则
,则
相比处于边界的网格S, 处于边角的网格T 则沿两个方向向环境传热, 同理可得出网格T 向环境传热的计算公式。
1.5 凝固潜热处理
每个网格代表的体积具有一定的内能。 在一般情况下,按照能量守恒定律,微元体的热平衡式可以表示为下列形式:(导入微元体的总热流量)+(微元体中内热源生成的热量)=(微元体内能的增量)+(导出微元体的总热流量)。
在此程序中通过研究每个网格能量的变化得到温度的变化:
式中,ΔQ 为网格热量的改变量;Q0 为当网格温度为T0 时相对于为绝对零度时单位体积具有的热量;Q1 为当网格温度为T1 时相对于为绝对零度时单位体积具有的热量。 当T0 大于等于熔点时,凝固潜热未释放:
当小于熔点时,凝固潜热释放完毕:
式(13~14)中,ρ 为物质的密度,kg/m3;c 为物质的比热容,J/(kg·K);γ 为物质的熔化热,J/kg;m 为质量,kg。
2 VBA 实现路径
2.1 程序设计思路流程图
本程序研究的是二维稳态导热问题,选取铸件某一截面后,将其划分为有限个网格,每个网格有一定的体积和物理性质, 网格在两个方向上有特定的长度(Δx=Δy),Microsoft Excel 中的1 个单元格代表1 个网格。 通过研究内部网格与网格间以及边界网格与环境之间的热量传输, 建立网格物理量的代数方程,基于VBA 使用Microsoft Excel 实现热量传输的迭代计算, 可以获得铸件截面的温度场和固相率。 程序设计思路如图3 所示,初始热量计算、实时温度计算以及固相率计算流程图见图4~6。

图3 程序设计思路流程图
Fig.3 Flow chart of program design
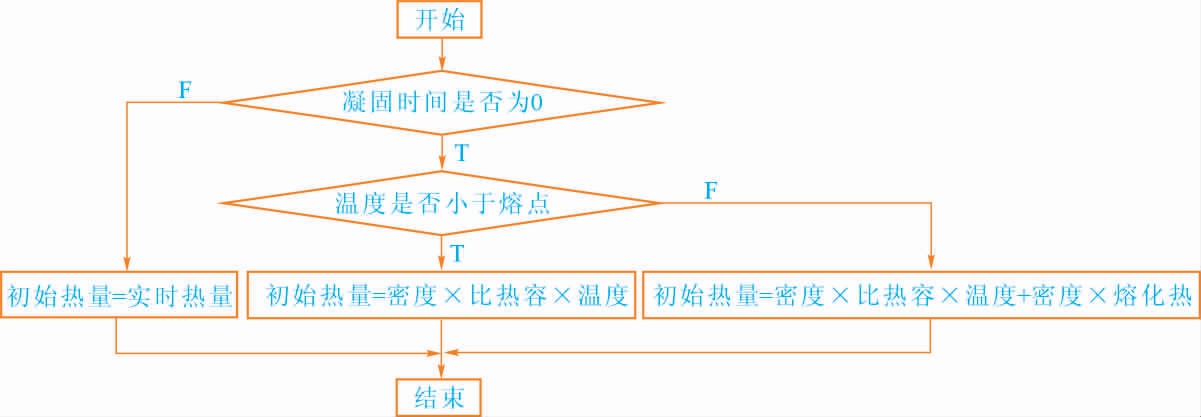
图4 初始热量Q0 计算流程图
Fig.4 Flow chart of initial heat Q0
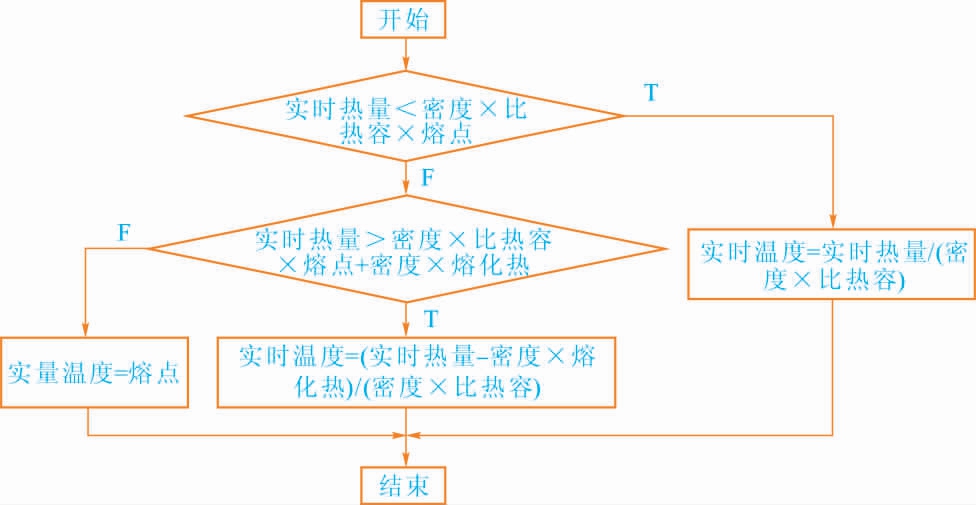
图5 实时温度Q1 计算流程图
Fig.5 Flow chart of real-time heat Q1
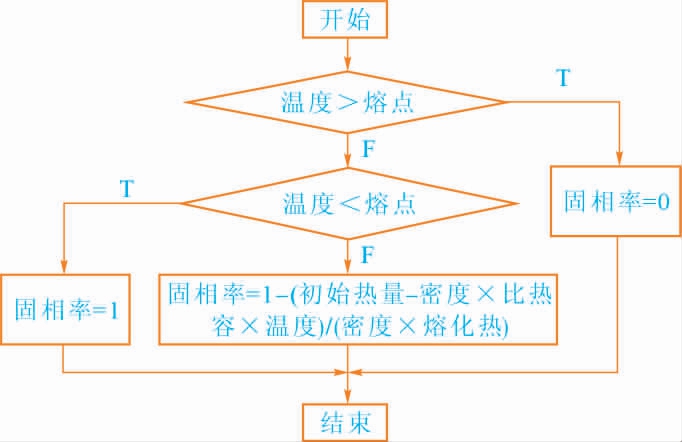
图6 固相率计算流程图
Fig.6 Flow chart of solid fraction
2.2 宏程序及执行
此程序涉及数据量较大的迭代计算,通过VBA编写宏程序,使工作表之间实现迭代计算,并能实现铸造凝固模拟的开始、暂停以及数据重置。 设计代码及执行如下:

宏“kaishi”是将工作表“实时温度T1”的值赋值给工作表”温度T”,以及使工作表“图表”中的“A2”单元格中的值与“A15”单元格中的值相加后再赋值给“A2”单元格,实现凝固时间的计算。

End Sub
宏“lianxu”是如果工作表“固相率L-S”中“A34”单元格的值不等于1 且工作表“图表”中“K8”单元格的值等于0 时,将连续执行宏“kaishi”,这能实现连续迭代计算。

宏“chonglai”是将工作表“初始温度T0”的值赋值给工作表“温度T”,并使工作表“图表”中“A2”单元格的值为0,这样就能使宏“lianxu”停止运行,并使图表恢复到迭代计算前的状态。

宏“zanting”使将1 赋值给工作表“图表”中的“K8”单元格,这样的话宏“lianxu”便不再满足执行的条件,运行将会停止。
为了方便使用宏,在工作“图表”中插入控件以使用不同的宏程序,获得简洁的操作界面。
3 算例具体实现过程
下面下举例说明铸造凝固模拟程序如何使用,所做假设如下:
(1)不考虑金属液的充型。
(2)金属液与型腔之间为理想接触。
(3)液态金属的热物理性质为常量。
铸件(图7)的尺寸为180 mm×60 mm×110 mm,取铸件中间的截面为研究对象, 浇注温度为1 883 K,环境温度为298 K。
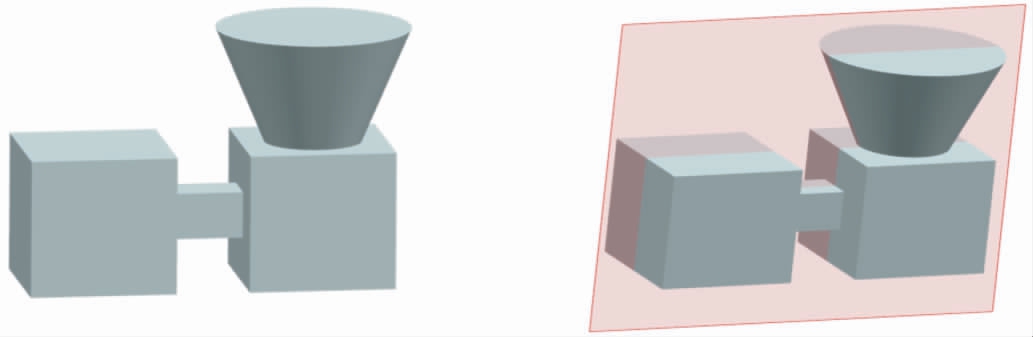
图7 铸件及其截面示意图
Fig.7 Schematic of casting and section
3.1 基本参数设定
分别建立工作表输入铸件材料和造型材料的导热系数、比热容、密度、熔点、熔化热及初始温度,这些工作表除了表示所用材料的热物理性质和环境条件外,还表示铸件截面的形状和尺寸。
假设每个网格的长度和高度为10 mm (即Δx=Δy=0.01 m), 砂型截面的长度和高度分别取320 mm和150 mm, 其对应的网格数分别是32和15 个,同理可得到铸件截面对应的网格数。表示砂型和铸件截面的网格分别用两种不同的颜色填充,一方面为了能够清楚、 直观地看出铸型和铸件截面的形状,另一方面方便之后的数据填充。 接着进行数据填充,手动输入工作量大,可以使用Excel 的“替换”功能,手动选择目标单元格的格式或直接点击目标单元格以获得其格式。 以导热系数为例,金属的导热系数为10 W/(m·K),铸型的导热系数为0.25 W/(m·K),实现一键填充。
另外, 金属材料和铸型材料的比热容分别为160、270 J/(kg·K),密度分别为7 500、1 600 kg/m3,熔点分别为1 783、2 000 K, 铸件材料的熔化热为65 000 J/kg。 同理,可使用“填充”功能将另几个工作表的数据填充上去,于是得到其他几张工作表。
3.2 热量传输
建立3 张新工作表,分别为“初始热量Q0”“热传导ΔQ”和“实时热量Q1”。先在每张工作表的1 个单元格中输入计算公式,再使用Excel 的“填充”功能将剩余单元格自动填充计算公式。
工作表“初始热量Q0”计算公式见图4;工作表“热传导ΔQ”的计算公式见式(7)和式(11)。 工作表“实时热量Q1”为工作表“初始热量Q0”与工作表“热传导ΔQ”相加所得。
3.3 温度场和固相率
建立工作表“实时温度T1”和“固相率L-S”,分别输入实时温度的固相率计算公式, 计算流程如图5~6 所示。
3.4 程序界面
为了能够直观、 清楚地观察到铸件凝固过程中温度场和物态的变化, 分别引用工作表“实时温度Tf”“固相率L-S”中的数据,在工作表“图表中”插入曲面图, 根据温度值和固相率值的变化范围设置图例大小,不同的图例大小填充不同的颜色。最后得到的程序界面如图8 所示。
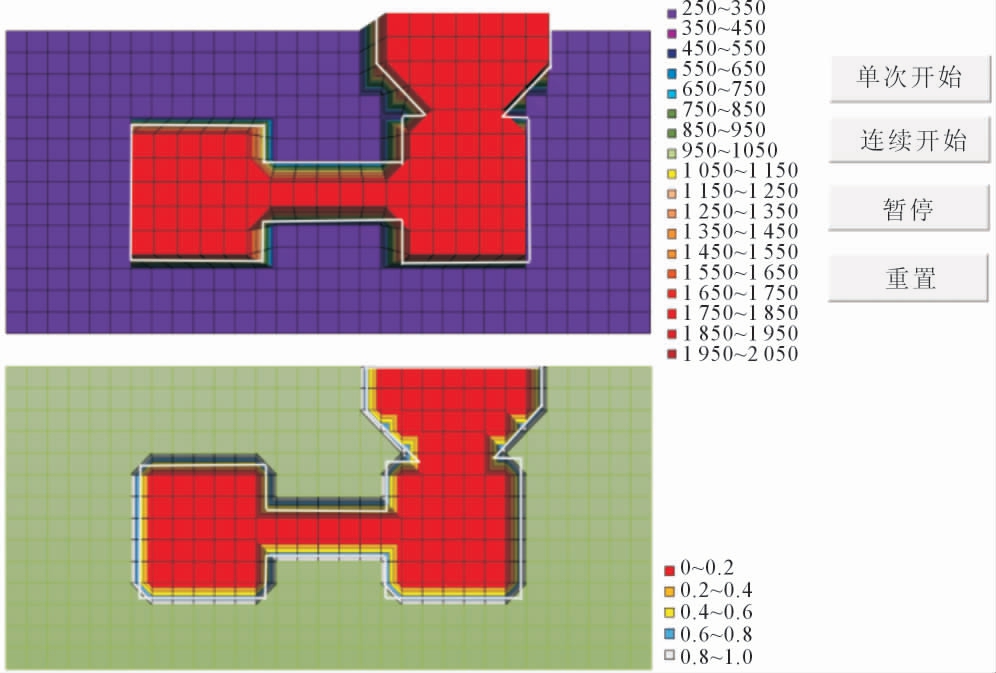
图8 程序界面
Fig.8 Program interface
3.5 模拟结果与讨论
凝固过程的温度场和固相率结果如图9 所示。由模拟结果可以看出此铸件在铸造凝固过程中左右厚大部位容易形成热节,铸件中间先凝固,厚大部位后凝固。 因此,厚大部位得不到及时补缩,铸件容易产生缩松、缩孔等缺陷,需要采取加冷铁改变铸件部位凝固顺序等措施避免缺陷的产生。
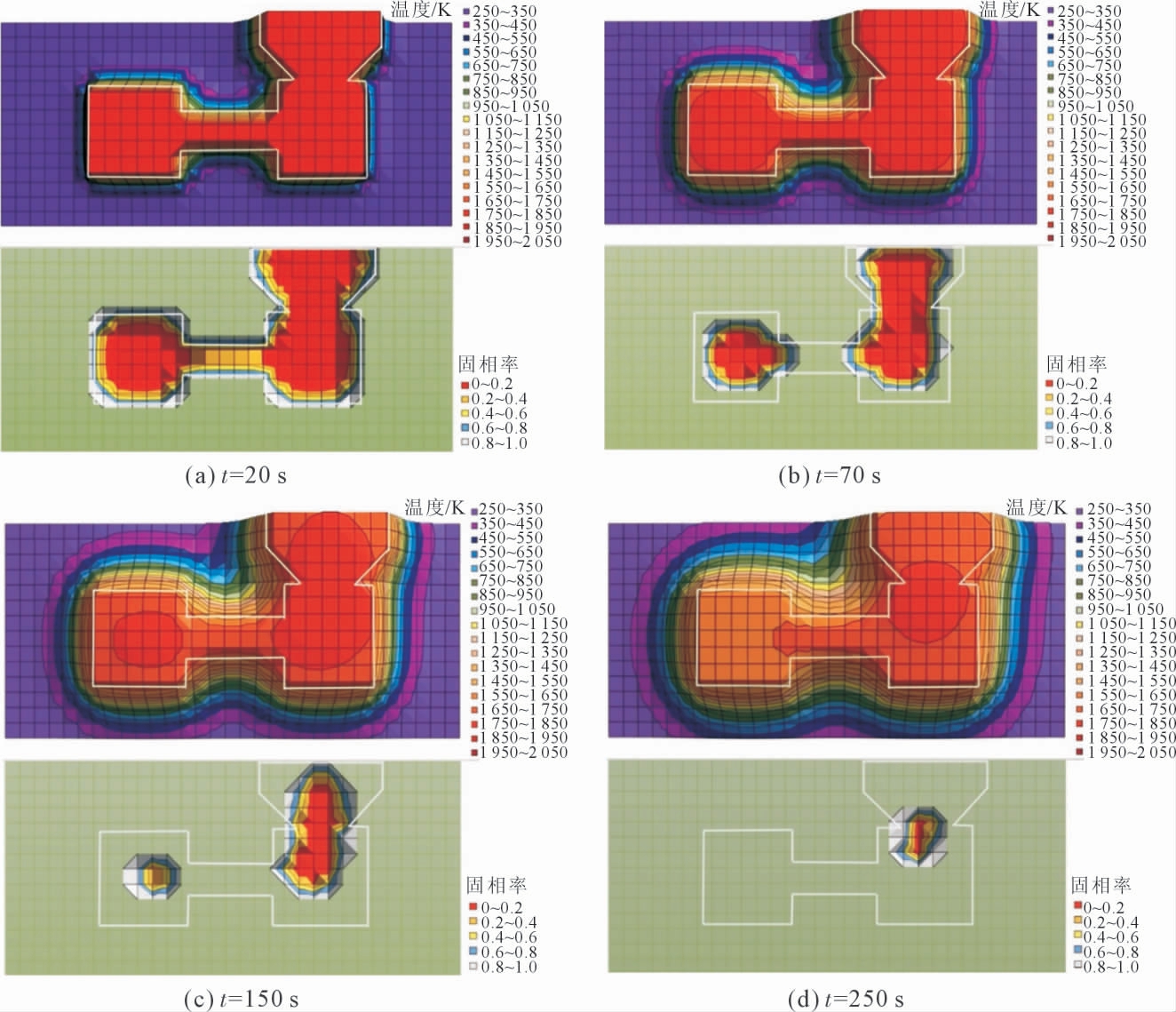
图9 温度场和固相率
Fig.9 Temperature field and solid fraction during solidification
此铸造凝固模拟程序能够进一步研究铸造过程中冷铁、涂料甚至气隙等对铸件凝固的影响。例如选取合适的冷铁或涂料的材料, 获取冷铁或涂料的导热系数,将其导热系数值填入工作表“导热系数k”,表达出冷铁大小、涂料层厚度,从而进行模拟计算。
4 结论
本铸造凝固模拟程序在Microsoft Excel 中利用传热过程控制方程的数值表达形式, 基于VBA 的宏程序,实现热量传输的迭代计算,研究铸件截面的二维导热问题。 此程序能够得到铸件截面的温度场和固相率,并通过图表反映温度场和固相率的变化过程,实现对铸件截面较为准确的铸造模拟。 虽然ProCAST,ANSYS,FlexPDE 等商业软件可以解决二维甚至三维导热的问题, 但基于VBA 的铸造模拟程序可以在Excel 表格中解决二维导热问题,而且通过深度开发并应用, 解决更加复杂的导热问题,甚至可以用来解决传质、流体流动、电流、机械应力等问题,具有广泛的应用前景。
[1] LIN P Z,LI N.Low pressure casting technology and forming process analysis of metal mold based on ProCAST FEA procedure[J].Mechanics of Advanced Materials and Structures, 2022, 29(9):1308-1315.
[2] ZUO C,WANG J,HE R D,et al.Casting simulation of fully welded ball valve core based on ProCAST[J].InternationalCore Journal of Engineering,2021,7(9):45-52.
[3] QIN S P, LV P, LI S R, et al. Casting process of gate valve steel based on ProCAST simulation[J].Journal of Physics: Conference Series,2021,1798(1):012013.
[4] 魏家强,程和法,程文. 基于ProCast 的熔模铸造安装座的应力模拟及裂纹分析[J].铸造技术,2022,43(1):19-23,27.
[5] 涂武涛,沈厚发,柳百成. 铸造凝固过程宏观偏析数值模拟研究[J].大型铸锻件,2014(2):1-3.
[6] 冀焕明,罗天骄,杨院生.AZ80 镁合金低压脉冲磁场半连续铸造过程的数值模拟和实验研究[J]. 中国有色金属学报,2017,27(3):468-476.
[7] 凌云,王红红,周建新,等. 钛合金离心铸造数值模拟技术及应用[J].铸造设备与工艺,2015(1):31-34.
[8] 郭钊,周建新,殷亚军,等. 基于改进差分网格的高温合金定向凝固数值模拟[J].特种铸造及有色合金,2019,39(6):613-618.
[9] 许庆彦,杨聪,闫学伟,等. 高温合金涡轮叶片定向凝固过程数值模拟研究进展[J].金属学报,2019,55(9):1175-1184.
[10] 王欢,王红红,周建新,等. 复杂钛合金铸件立式离心铸造过程的数值模拟[J].特种铸造及有色合金,2015,35(2):178-181.
[11] 邵珩,李岩,南海,等.Ti-6Al-4V 合金熔模铸造过程中的固态相变微观组织演变的数值模拟[J]. 金属学报,2017,53(9):1140-1152.
[12] 吴树森.材料加工冶金运输原理[M]. 北京: 机械工业出版社,2018.
[13] Luis García Blanch. Two-dimensional modeling of steady state heat transfer in solids with use of spreadsheet (MS EXCEL)[D].Poland:University of Bielsko-Biała,2011.