疲劳裂纹扩展速率是指在疲劳荷载作用下裂纹长度随循环周次的变化率,也是决定构件疲劳行为的重要特征参数,反映了裂纹扩展的快慢。根据GB/T 6398-2017 《金属材料疲劳试验疲劳裂纹扩展方法》[1]推荐,常采用割线法和递增多项式法对疲劳试验数据进行处理。上世纪,英国学者Smith 提出了一种数据处理方法即Smith 法[2]。对于上述几种试验数据处理方法,国内外学者持有不同的意见。贾法勇等[3]通过七点递增多项式法和Smith 法对20MnHR焊缝与热影响区的疲劳裂纹扩展速率进行了对比分析,发现不同的数据处理方法得到的结果不同;在较大范围的疲劳裂纹扩展区域内,七点递增多项式法具有更高的安全系数。
关于常用钢材的疲劳裂纹扩展试验已有不少学者进行了研究[4-9]。60Si2Mn 弹簧钢常用以制造高速铁路轨道扣件[10-11],热处理后的60Si2Mn 弹簧钢具有更高的屈服强度和抗拉强度,同时有着更好的弹性和耐腐蚀性[12-14]。为探究热处理对60Si2Mn 弹簧钢疲劳裂纹扩展速率的影响,本文采用割线法、递增多项式法和Smith 法3 种疲劳试验数据处理方法,探讨不同数据处理方法的差异,对比分析60Si2Mn弹簧钢调质处理前后的疲劳裂纹扩展规律。
1 疲劳裂纹扩展速率实验
疲劳试验采用标准的紧凑拉伸C(T)试样[1],如图1 所示,60Si2Mn 弹簧钢疲劳试样名义厚度12.5 mm,试样宽度50 mm,预制疲劳裂纹长度1.5 mm。调质处理工艺为:在870±20 ℃对试样在油中淬火后再进行回火处理,回火温度480±50 ℃。60Si2Mn 弹簧钢的力学性能如表1 所示,满足国家标准GB/T 1222-2016《弹簧钢》[15]的要求。
表1 60Si2Mn弹簧钢的力学性能
Tab.1 Mechanical properties of 60Si2Mn spring steel
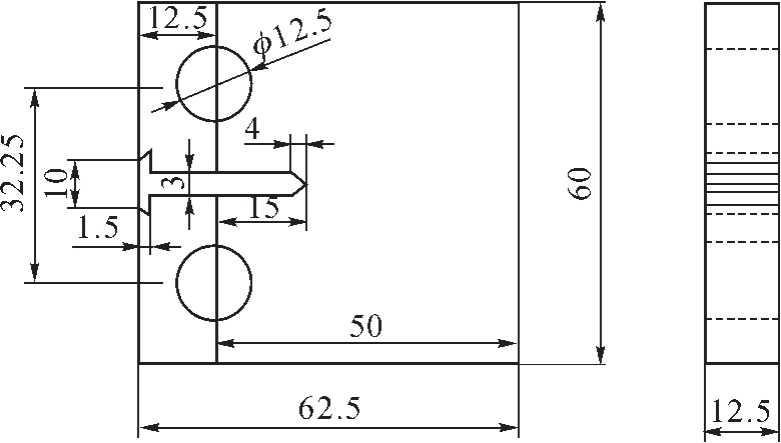
图1 C(T)试样
Fig.1 C(T)sample
在MTS 810 电液伺服疲劳试验机上进行疲劳试验,试验应力比R 为0.1,即裂纹稳定扩展阶段中最大荷载Pmax=7 kN,最小荷载Pmin=0.7 kN,加载频率为20 Hz。在试样开口处放置引伸计,基于柔度法测量裂纹扩展长度。柔度法表达式为:

基于线弹性断裂力学,对式(2)所示的Paris 公式两边取对数,即可得到疲劳裂纹扩展速率da/dN与应力强度因子幅度ΔK 的关系,如式(3)。

2 疲劳裂纹数据处理方法
(1)七点递增多项式法 在测量裂纹扩展速率试验中,有恒载增K 试验和降K 试验,而七点递增多项式法仅适用于增K 法,其主要原理是将原始数据的局部数据点拟合成一个多项式。即对任意数据中的点i 前后各N 点,共(2N+1)个连续数据点,采用式(4)进行拟合求导,N 的取值可为2,3,4。当N 取值为3 时即为七点递增多项式法。

其中系数b1、b2、b3 是在区间[ai-3,ai+3]上按照最小二乘法确定的回归参数,拟合值ai 是对应循环数Ni 上的拟合裂纹长度。
对式(4)求导即可得到Ni 处的裂纹扩展速率,如式(5)所示。
(2)割线法 割线法仅适用于计算相邻两个裂纹长度和循环周次数据对的直线斜率,但其计算方法方便,计算速度快捷,也常应用于疲劳裂纹扩展速率的计算之中。割线法的具体计算式为:
式中,a(j)avg 为平均裂纹长度,其表达式为:
(3)Smith 法 Smith 法是将m 对试验数据(Ni,ai)转换成(yi,xi)进行计算,具体表达式为:
式中,yi=Ni-N1,xi=ai/a1,系数b0、b1、b2 可通过最小二乘法得出。
对式(8)求导可得到疲劳裂纹扩展速率为:
3 实验数据处理及分析
相比于单试样数据处理方法,成组数据处理方法是将同种试样的(da/dN)i 和ΔKi 数据点整理成一组数据,再在双对数坐标下进行线性拟合。成组数据处理可以避免单试样数据处理时局部误差给数据结果带来的影响。本文采用成组数据处理方式,对比割线法、递增多项式法和Smith 法3 种疲劳试验数据处理方法的差异性。
将所计算的结果(da/dN)i 和ΔKi 绘制与双对数坐标中,如图2 所示。用最小二乘法进行线性回归分析,求得式(2)所示的Paris公式中的C 和m 值如表2 中所示。
表2 疲劳裂纹扩展速率拟合结果
Tab.2 Fatigue crack propagation rate fitting results


图2 不同疲劳试验数据处理方法下的拟合结果
Fig.2 Data fitting results under different data processing methods
3.1 疲劳实验数据处理方法的对比
相关系数表示变量间的线性相关性的强弱,其值越接近于1,表明其相关性越强,拟合效果越好。对比表2 中3 种数据处理方法的相关系数发现,七点递增多项式法的拟合效果最好,Smith 法拟合效果次之,割线法的拟合效果相对较差。这是由于七点递增多项式法是将前后七个数据点考虑为一组进行拟合,考虑了每一组数据点的前后三个数据,即使一种数据中有误差数据也不会对整体的拟合带来较大的影响;Smith 法是对整体数据进行拟合,然后在每一组数据点上进行求导得到裂纹扩展速率,在裂纹扩展后期表现出了一定的波动性;割线法是采用前后两点之间的平均速率代替前后两点之间中点的速率,所以割线法在疲劳裂纹扩展曲线中表现出了相对较大的摆动性。
由图2 和表2 可知,七点递增多项式法数据点离散性较小,可以更好的反应疲劳裂纹扩展速率。由于七点递增多项式法和Smith 法均需要进行相应的编程处理,标准推荐了更为简便的割线法。虽然割线法离散性较大,拟合精度较差,但如本文拟合结果所示,其拟合结果与另外两种方法相差不大,对于试验数据的粗略处理更为方便。
3.2 60Si2Mn 弹簧钢的疲劳裂纹扩展速率
由上述结果可知,热处理前60Si2Mn 弹簧钢的疲劳裂纹扩展曲线相比于热处理后的曲线更加陡峭。60Si2Mn 弹簧钢的应力强度因子幅值ΔK 为50 MPa·m1/2 左右,而调质处理后应力强度因子幅值提高,其ΔK 大于90 MPa·m1/2。这表明热处理前,60Si2Mn 弹簧钢抵抗疲劳的能力弱,疲劳裂纹扩展速度快并在后期表现出快速断裂的情况。
由表2 可知,无论采用那种疲劳试验处理方法,结果均表明调质处理后60Si2Mn 弹簧钢的m 值小于未热处理的,而C 值大于未热处理的。调质处理后,60Si2Mn 弹簧钢的疲劳裂纹扩展速率曲线曲线更加平缓,表明疲劳裂纹扩展速率增加的更加缓慢,抵抗裂纹扩展的能力更强。
综上所述,考虑七点递增多项式法可以更好的反应60Si2Mn 弹簧钢的疲劳裂纹扩展能力,得到热处理前后的表征60Si2Mn 弹簧钢的疲劳裂纹扩展的Paris 公式分别为:
4 结论
本文对热处理前后的60Si2Mn 弹簧钢材料进行了应力比为0.1 的疲劳裂纹扩展试验,采用不同成组数据处理方式进行数据处理并对比其差异性,得出结论如下:
(1)割线法,七点递增多项式法和Smith 法3 种疲劳试验数据处理方法均可以较好拟合60Si2Mn弹簧钢的疲劳裂纹扩展试验数据。其中七点多项式法拟合精度高,拟合效果最好。
(2)调质处理后,60Si2Mn 弹簧钢的疲劳裂纹扩展速率曲线更加平缓,抗疲劳裂纹生长的能力更强。
(3)利用七点多项式法确定了60Si2Mn 弹簧钢的Paris 公式中的材料常数m 和C。其中热处理前,60Si2Mn 弹簧钢的m 为3.368 8,C 为1.775×10-12;调质处理后的m 为2.9878,C 为7.119×10-12。
[1]全国钢标准化技术委员会:金属材料疲劳试验疲劳裂纹扩展方法:GB/T 6398-2017[S].北京:中国标准出版社,2017.
[2]SMITH R A.The determination of fatigue crack growth rates from experimental data[J].International Journal of Fracture,1973,9(3):352-355.
[3]贾法勇,霍立兴,张玉凤,等.疲劳裂纹扩展速率两种数据处理方法的比较[J].机械强度,2003,25(5):568-571.
[4]宗亮,施刚,王元清,等.Q345qD 桥梁钢疲劳裂纹扩展速率试验研究[J].中国铁道科学,2015,36(3):37-44.
[5]王春生,段兰,郑丽,等.桥梁高性能钢HPS 485W 疲劳裂纹扩展速率试验研究[J].工程力学,2013,30(6):212-216.
[6]廖小伟,王元清,石永久,等.低温环境下桥梁钢Q345qD 疲劳裂纹扩展行为研究[J].工程力学,2018,35(10):85-91.
[7]周小林,向延念,陈秀方.U71Mn 50 kg·m-1 普通碳素钢钢轨疲劳裂纹扩展速率试验研究[J].中国铁道科学,2004(3):87-91.
[8]XIAO K,LIU P,SUN S Y,et al.Study on fatigue crack propagation and fracture characterization of 7050-T7451 friction stir welded joints[J].Journal of Materials Engineering and Performance,2021,30:5625-5632.
[9]曾维虎,周晓明,冯业飞,等.固溶处理和疲劳保载时间对FGH96 合金高温疲劳裂纹扩展速率的影响[J].铸造技术,2020,41(4):366-369.
[10]黄新杰,伍曾,张景坤.高速铁路弹条疲劳对其扣压力的影响[J].铁道建筑,2020,60(2):134-136,147.
[11]聂小龙,高加强,孟开仁,等.60Si2Mn 弹簧钢弹簧钢的断裂失效分析[J].金属热处理,2021,46(8):246-250.
[12]焦志强.热处理工艺对60Si2Mn 钢弹性挡圈性能的影响[J].金属热处理,2018,43(5):153-156.
[13]周青松,郝庆国,杨旗,等.淬火分配工艺对60Si2Mn 弹簧钢显微组织和力学性能的影响[J].机械工程材料,2021,45(1):14-19,27.
[14]孟令涛,窦坤,卢新春,等.含硼60Si2Mn 弹簧钢的热处理工艺优化[J].金属热处理,2017,42(7):126-131.
[15]全国钢标准化技术委员会.弹簧钢:GB/T 1222-2016[S].北京:中国标准出版社,2016.