现代合金材料要在极端条件下保持高性能,需要加入较多合金元素满足特定需求(如耐高温的镍基合金,钴基合金)。然而,其凝固过程中形成的夹杂物、偏析及其凝固组织都对其性能有很大影响。在调整常规生产工艺参数外,电磁冶金技术已成为生产高性能合金材料的一种很重要的手段。电磁冶金技术将各类电磁场应用于冶金过程中,通过其电、磁、热、力等效应调控冶金工艺过程。利用这些物理效应,目前已开发出如:钢液中施加电磁净化技术(去除夹杂);中间包施加电磁加热和净化技术(控制温场、流场、去除夹杂);水口中施加电磁旋流技术(降低对结晶器内钢液的冲击);结晶器中施加软接触电磁连铸(减少结晶器振痕);施加板坯结晶器电磁搅拌技术(减少钢液中气泡与夹杂物、均匀钢液成分)[1]。电磁感应加热技术作为一种电磁冶金技术,早在20 世纪50 年代已进入工业应用。20 世纪60 年代已开展磁场控制金属流动的研究,其后电磁搅拌技术开始应用于工业中。1982 年,国际理论及应用力学协会召开了国际会议“The Application of Magnetohydrodynamics to Metallurgy”,随后法国、英国、日本、德国、中国等分别成立了专门的机构推动电磁冶金及材料制备技术的发展[1]。21 世纪后,随着超导磁体技术发展,超导强磁场在冶金过程中的应用受到广泛关注,并在电磁场流动控制、电磁净化、静磁场下凝固、电磁场下磁致过冷、磁致塑性、磁场影响扩散等多个方面取得显著进展[2-3]。
然而,电磁冶金技术仍然需要进一步优化工艺,而通过数值模拟仿真可以全面的分析整个区域内不同时刻的温度场、流速场、溶质分布场、电磁场,能够通过可视化技术更直观的理解并针对性提出改进方案,因此对电磁冶金过程进行数值模拟可以辅助工艺参数的探索。此外,通过数值模拟可再现出磁场下的凝固、流动等物理过程,是进一步从底层理解并发展电磁冶金技术的必要手段。本文旨在对近年来电磁场等多物理场下金属凝固模拟研究进行总结,分析模拟计算面临的难题,讨论需要进一步发展的方向。
1 电磁冶金宏观模拟(Macroscopic simulation)
电磁冶金过程本质上是多物理场下的凝固过程,其涉及多尺度下多种物理过程的交互(如不同尺度下的电场、磁场、流场、温度场、溶质场、应力场、界面形貌之间的交互)。在全尺度下第一性的计算出所有物理过程,对目前的计算设备来说是不可能的,因此需要对不同尺度的物理过程分别建模计算并分析。近年来,多物理场凝固模拟方法一直在发展中,但与实际电磁冶金工程问题结合的大多是宏观尺度模型(无法直接计算出凝固组织),而微观介观尺度模型由于其应用尺度限制较难直接与工程问题结合。本小节仅讨论近年来宏观尺度的多物理场凝固模拟研究。
1.1 连铸过程模拟
连铸过程中原本就时刻存在熔体流动,因此电磁场下连铸模拟多是研究电磁搅拌、电磁制动对连铸流动过程的影响。求解方面多使用有限元求解电磁场,有限体积求解流场,使用焓-多孔模型以及达西源项(Darcy source term)来处理宏观固液界面。
Toh 等[4]用迭代法数值求解在电磁场下连铸模具和浇注口之间所形成的弯液面形状。通过传热计算得到的凝固坯壳和电磁场影响下的弯液面,计算出了流场分布。流体的控制方程为Navier-Stokes 方程和连续性方程,采用边界拟合的有限差分法进行分析。同时,采用k-ε 模型描述湍流,并在凝固前沿采用壁面函数,弯液面采用自由边界,来模拟不锈钢圆坯的连铸凝固过程。Kim 等[5]开发了电磁制动(Electromagnetic brake,EMBr)板坯连铸过程中传输现象的三维稳态守恒方程的计算机程序,研究了EMBr对熔体湍流流动、温度场对金属液宏观凝固的影响。根据多孔介质的达西定律,根据焓-孔隙关系,给动量方程添加一项作为阻尼源项,以考虑糊状区对流动的抑制。糊状区潜热释放的处理方法依赖于基于单域的焓法。电磁场由麦克斯韦方程描述。流动方程、电磁方程均由有限体积法离散,并用显式迭代法迭代。电磁通过电磁力的方式加入到流动方程的源项中。加入电磁制动使得出口边界没有出现回流,降低了结晶器附近的流速,使结晶器下方流动更加均匀,提高了凝固壳附近的温度梯度。Li 等[6]为提高连铸时电磁制动的效率,建立了分析金属液流动的数学模型。采用k-ε 湍流模型,并将电磁力引入到Navier-Stokes 方程中,来计算电磁力对流动的影响,并基于FORTRAN 开发了模拟计算工具。当氩气注入模具时,气体强化了模具上部湍流的强度。当在模具和浇注口之间所形成的弯液面以及喷嘴下方施加两个磁铁时,体块中的速度被显著抑制。
Yamazaki 等[7]建立了0.7 wt.%铁碳合金连铸过程凝固组织形成的数值模型。该模型将元胞自动机方法与连铸过程的传热计算相结合。CA 方法基本基于Rappaz 和Gandin 等人,但是采用了一种更为简单的形核模型。为了评价电磁搅拌(Electromagnetic stirring,EMS)引起的流体流动对钢坯热流的影响,该文通过改变热导率将流体流动的影响纳入传热计算。在这种方法中,有EMS 的钢液表观热导率比没有EMS 的钢液表观热导率大。Song 等[8]应用三维非定常数学模型,对电磁搅拌连铸钢液的湍流流动、温度场和宏观凝固过程进行了模拟。研究了流体流动引起的感应电流和搅拌器末端效应。同时也考虑了感应电流引起的洛伦兹力和焦耳热。该模型在低雷诺数近似下,外部旋转磁场的计算可以与流体流动分开处理。用焓-孔隙率关系来估计糊状带内的速度。应用SIMPLE 算法求解Navier-Stokes 方程。磁场应用有限元离散求解,流场应用有限体积法求解。
Yang 等[9]基于CFX 商用软件和事先编制的Fortran 程序,来模拟连铸过程中结晶器电磁搅拌的过程。湍流使用k-ω 模型引入。在他们的计算模型中,将坯料内的浆液区视为多孔介质,并在控制方程中加入达西源项。采用有限元法和有限体积法分别求解三维电磁场数学模型和流动凝固模型。电磁方面针对连铸过程的特性,将完整的麦克斯韦方程组进行了简化(公式(1~4)),并依照算出的电磁场推出作用在流体上的力(公式(5))并作用于动量方程。

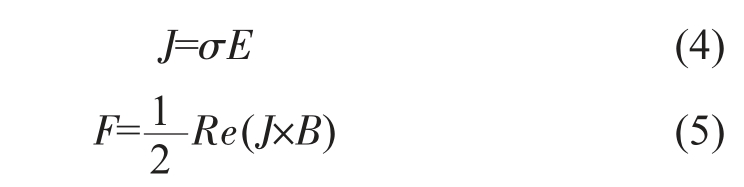
式中,H 为磁场强度,J 为电流密度,B 为磁感应强度,μH 为磁导率,E 为电场强度,σ 为电导率,Re 为实部算子,F 为洛伦兹力。
他们基于该模型研究了不同电流强度下结晶器内流动以及凝固行为,如图1。模拟结果显示,更强的电流带来更强的液相流动,有利于增加等轴晶区比例,但是过大的电流会导致凝壳厚度波动,因此电磁搅拌应注意选取合适的电流。
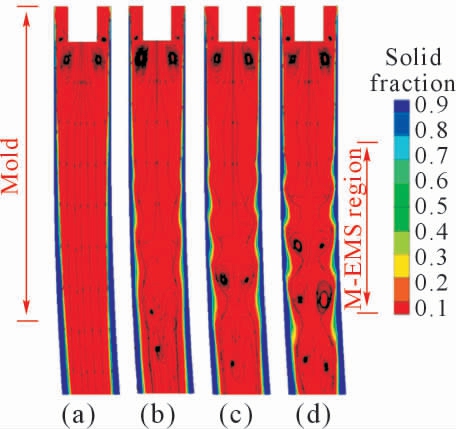
图1 不同电流强度的电磁搅拌下结晶器内流场[9]
Fig.1 Streamlines and contour of flow in mold under electromagnetic stirring of different current intensities[9]
Wang 等[10]以连铸方坯结晶器为研究对象,利用ANSYS 和fluent 软件,采用有限元和有限体积法相结合的方法,通过自编程将磁场数据导入到FLUENT 的MHD 模块中,进行磁场、流场和温度场的三维耦合计算,研究了电磁搅拌对钢液流动和传热的影响,并对钢的凝固组织进行了测试。结果表明电磁搅拌器能很好地达到提高等轴晶比和碳宏观偏析指数的目的。Shvidkiy 等[11]利用有限元软件COMSOL Multiphysics 对铝锭液相电磁搅拌连铸过程中的流体力学、电磁和热过程进行了建模并求解。其中液相流动用NS 方程进行描述,利用麦克斯韦方程组解磁势。计算出凝固前沿的温度梯度,进而得出对结晶过程的影响。Ren 等[12]建立了大方坯连铸结晶器电磁搅拌结晶器连铸的三维数学模型,研究了搅拌电流对诱导流动特性、传热和凝固的影响。通过求解麦克斯韦方程组计算连铸结晶器内电磁场,通过求解Navier-Stokes 方程和能量方程研究了结晶器内熔体的流场和温度分布。模拟结果如图2,电磁搅拌产生的旋流阻止了水口向下流动的过热射流,随着搅拌电流的增大,旋流增强,延长了熔体在结晶器中的停留时间,结晶器内熔体温度随之升高,凝固前沿温度梯度的增大,有助于扩大等轴带。
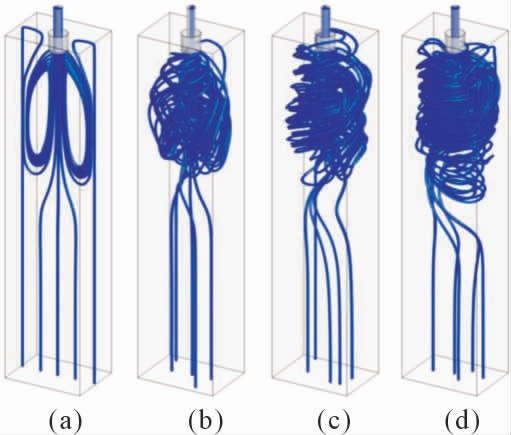
图2 不同电流强度的电磁搅拌下结晶器内流场[12]
Fig.2 Streamlines and contour of flow in mold under electromagnetic stirring of different current intensities[12]
Yin 等[13]为了研究板坯连铸过程中夹杂物的捕获问题,建立了流场、凝固过程和夹杂物运动的三维耦合模型。此外,为了研究结晶器内电磁搅拌对大夹杂物捕获的影响,还将电磁场耦合到模型中。流动采用k-ε 方法,并采用有限体积法离散。该文采用焓-孔隙法模拟传热和凝固过程,将糊状区域视为伪多孔介质,研究了有无电磁搅拌对结晶器内流场的影响,并通过夹杂捕获模型分析了电磁搅拌对夹杂物捕获的影响。模拟结果表明(图3),当电磁搅拌偏置时,结晶器内两侧流场一侧被促进,另一侧被抑制。Fang 等[14]基于商用计算流体力学软件ANSYS FLUENT 对U71Mn 钢坯连铸结晶器区熔体流动、液面波动、温度场以及电磁搅拌作用下的凝固行为进行了数值分析。传热模型采用焓方法计算温度场和凝固过程。该文采用流体体积法(VOF)对结晶器内钢/渣界面波动进行跟踪,该方法通过求解一组动量方程,在整个区域内跟踪每种流体的体积分数,从而对两种或两种以上不混相流体进行建模。黏度和热导率是预测钢的流动和凝固行为的重要热物性参数,尤其是在糊状区。黏度和导热系数随局部温度的变化由JMatPro7.0 软件计算。随后研究了水口结构和优化后的四口喷管安装方式对金属熔体结晶器内流型、液位波动、传热和初始凝固行为的影响。实验和数值模拟结果表明,优化后的斜置四端口水口不仅可以缓解钢液水平波动,降低对壁面的冲击压力,改善钢液的流动形态,也有利于消除撞击效应导致的局部凝固壳变薄现象。

图3 不同位置电磁搅拌下结晶器内流场[13]
Fig.3 Streamlines and contour of flow in mold under electromagnetic stirring of different current position[13]
Guan 等[15]为了研究复合EMS(M-EMS+F-EMS)模式对连铸重轨钢坯宏观偏析的影响,建立了基于体积平均欧拉法的三维多相凝固模型,模拟了不同EMS 模式下重轨钢坯的电磁场、流体流动、组织演变和溶质运移过程。在传质模型源项中加入动态枝晶生长模型,模拟连铸过程中的微观组织演化过程。通过在溶质输运模型的源项中考虑反扩散模型,改进了宏观偏析的精度。模型中引入了Ilegbusi提出的混合模型,以更准确地描述糊状区域内的流体流动。微观结构演化用CA 法进行描述,根据元胞自动机的概念,建立了连铸过程中柱状枝晶的动态生长模型。柱状晶的生长基于KGT 模型,等轴晶的生长基于高斯KDE 模型进行描述。利用Fluent 软件实现了多相凝固模型中各子模型的耦合计算,揭示了连铸过程中熔体流动、传热、溶质输运、晶粒形核和长大等现象。不同EMS 工艺下的实验结果与数值模拟结果吻合较好,证明了多相凝固模型的准确性和可靠性。周然等[16]在低熔点金属物理模拟的基础上,利用标准k-ε 模型对板坯连铸电磁制动的结晶器流场进行了数值模拟,所得到的基本流态、主流场,与物理模拟实验的结果相符。结果显示,就弯月面流速、液流对结晶器窄面的冲击强度而言,EMBr-Ruler 和FC Mold 电磁制动均有良好的效果。对液面流速而言,EMBr-Ruler 电磁制动会增大液面流速,而FC Mold 电磁制动则对结晶器内液面流速的抑制作用明显。EMBr-Ruler 电磁制动有利于融渣,但应注意卷渣;而FC Mold 电磁制动则有利于除杂,但不利于融渣。
1.2 模铸过程模拟
模铸过程中原本熔体流动较弱,因此电磁场下的模铸模拟,大多是研究外场引起的流动对凝固过程的影响。求解方面与上述连铸过程类似,多使用有限元、有限体积、焓-多孔模型来耦合分析。
在模铸应用方面,Kageyama 等[17]提出了针对电磁铸造数学模型。该三维模型计算了电磁场、液态金属湍流流动和熔体自由表面随时间的演化。同时求解麦克斯韦方程组,欧姆定律,Navier-Stokes 和连续性方程(大涡模拟)和自由面方程。自由表面变化在欧拉-拉格朗日网格上结合有限元(场和流方程)和有限差分(自由面方程)方法进行求解。流动方程采用混合单元格式,即单元节点处计算速度,单元中心处计算压力。流动微分方程的离散化使用流线迎风/Petrov-Galerkin 方法来表示对流项。该模型的软件基于FORTRAN77 编写,并与其他数值模拟工作进行了验证。Chaudhary 等[18]研究了磁场对金属液在方腔中流动的平均速度以及湍流参数的影响,表征了三维瞬态流动。以往的研究基于雷诺时均,难以全面分析凝固时磁场对湍流行的影响,因此使用了直接数值模拟DNS 进行计算。用分数步长法求解了压力-速度耦合问题,用多重网格求解了压力泊松方程。由于液态金属具有较低的磁雷诺数,因此忽略了感应磁场。在验证了程序的正确性后,用不同的哈特曼数对方形管道内的湍流流动进行了计算,直到流场完全分层。通过平均速度、湍流波动、涡度和湍流动能收支的分布,研究了流动速度的时间依赖性和时间平均性质(图4)。
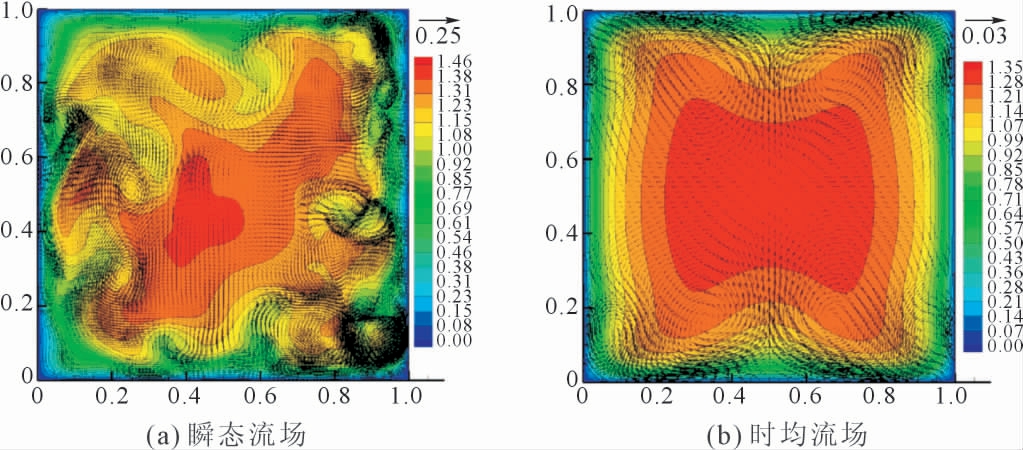
图4 电磁场作用下的瞬时和时均速度场[18]
Fig.4 Instantaneous and time-averaged velocity fields under electromagnetic field[18]
Bermúdez 等[19]对电磁场驱动下的液态金属流动进行了数值模拟。使用磁标量势的积分以及适当的金属边界渐进处理来计算模具和浇注口之间所形成的弯液面形状。将电磁场计算与弯月面形状计算通过迭代法求解。对瞬态Navier-Stokes 方程使用隐式格式进行时间离散化,使用速度/压力的混合变分公式,并在CEM2D 软件中实现了数值算法。该模型的主要创新之处在于使用渐近展开法来计算磁感应,使得金属所占据的区域可以从计算域中去除。Duan 等[20]研究了不同占空比的脉冲磁场(Pulsed magnetic field,PMF)对大尺寸镁合金方坯直冷铸造过程中熔体流动和传热行为的影响,找出合适的占空比范围。磁场与温度场和流体流动的相互作用的计算采用单独的步骤完成。基于有限元法,利用COMSOL Multiphysics 和Matlab 软件对多物理场耦合进行求解。结果显示在PMF 作用下,熔体振动是由于洛伦兹力的反复推拉作用的瞬时冲击产生的。随着占空比的增大,洛伦兹力的峰值大大减小,但熔体波动区域扩大,熔体内部速度加快,液固界面温度梯度减小。然而占空比过高的PMF 对熔体对流有不利影响,对内部熔体的影响有限。占空比为20%~50%是一个合理的范围。Drezet 等[21]通过对铝合金板坯直接冷铸(DC)和电磁铸造(EM)过程中铸锭变形的预测,优化生产扁平铸锭的模具/感应器形状。该文利用有限元软件ABAQUS 建立的瞬态热力模型预测了直流/电磁铸造过程中的变形和温度场演变。固体中的变形假定遵循黏塑性定律。根据第一部分的测量结果对该模型进行了验证。该模型能够预测铸造参数对DC 铸锭和EM 铸锭的焊头弯曲和膨胀、轧制面拉入和残余应力状态的影响。
Hatic'等[22]提出了一种无网格数值模拟低频电磁铸造宏观偏析的新方法,并对模拟结果进行了分析。铸造模型包括一组耦合的质量,动量,能量和物质守恒方程。利用感应方程计算了洛伦兹力,并将其应用于凝固模型中。该耦合物理模型在柱坐标系下求解,可用于铝合金坯料生产的模拟。时间离散采用显式格式,空间离散采用无网格扩散近似方法。该方法被本地化为包含14 个本地节点的子域。加权最小二乘最小化方法采用高斯权重。采用体积平均法来编写固液两相问题的守恒方程。在熔体中,规定各处固体的速度,液相是不可压缩的牛顿流体。熔体的黏度是恒定的,流动状态假定为处处呈层流。采用Boussinesq 近似来模拟由于密度差异引起的浮力效应,同时假定固相和液相的密度恒定且相等,在多孔介质开始凝固时,界面阻力项采用达西方程来模拟。Al-5.25 wt.%Cu 的材料性能由JMatPro 提供。计算结果表明,电动势对熔体流动和凝固有较大影响。在电磁铸造的某些几何形状中,得到了振荡非稳态的解。由于铸造几何、铸造参数和EMF 参数的强耦合作用,不使用数值模拟很难预测EMF 的影响。这表明需要对这个强耦合问题进行数值模拟,以便更好地理解该过程。
Sha 等[23]为研究电磁搅拌对Al-Ni 合金铸锭凝固过程的影响,采用数值模拟方法对真空条件下Al-50Ni 合金的电磁搅拌凝固过程进行了描述,并建立了三维数学模型。利用ANSYS 软件对电磁场进行模拟,利用FLUENT 软件对热流场进行模拟。通过自定义子程序实现了电磁场与热流场的耦合,采用动态黏度来表示凝固对流动的影响。电磁方程和运动方程均由有限元方法求解。结果表明,电流强度对流体流动和合金组织有显著影响。实验条件下的最佳电流强度为80 A,最佳频率为50 Hz,模拟结果与实验结果吻合较好。Le 等[24]利用ANSYS 软件建立了镁合金电磁直流铸造模型,研究了镁合金在有无电磁场的情况下直流铸造的流场和温度场,并对交变电流的交变频率和电磁场的穿透深度对涡流的扰动进行了研究。仿真结果表明,在相同铸造条件下,施加电磁场后,涡旋搅拌产生的强制对流会导致较低的温度梯度,促进晶粒细化和等轴晶粒的形成。同时由于洛伦兹力的作用,降低了接触压力,提高了坯料的表面质量。
1.3 定向凝固过程模拟
定向凝固过程生长速度较慢,流动主要为自然对流,因此电磁场下定向凝固模拟多是研究电磁制动对凝固过程的影响;另外定向凝固过程各物理场分布较为简单,适合探究电磁冶金作用的机理。
Wang 等[25]通过同步辐射原位实验等表征手段,研究了静磁场下热电磁对流对定向凝固过程的影响。在金属凝固过程中,施加静磁场与热电流(TEC)相互作用,会在熔体中产生流动(热电磁流动)。通过有限元软件COMSOL Multiphysics 耦合传热、电流和流体流动过程并进行三维数值模拟,探究不同磁场条件下的电磁流动对定向凝固过程的影响。无磁场模拟结果表明(图5),热电流在合金凝固过程中自然存在,通过液相和固相流动,并通过界面闭合。在磁场辅助算例中,热电流与外加磁场相互作用可产生热电磁流动。通过非原位实验、原位观察和模拟,系统研究了横向静磁场辅助定向凝固中热电磁流动及其对固液界面形状的影响。对轴向静磁场作用下的热电磁流动进行了计算,揭示了该流动围绕枝晶环形流型的行为方式。实验结果与模拟结果吻合较好,证实了热电磁流动的存在及其对固液界面形状的影响。Zhong 等[26]对铝铜合金定向凝固过程中枝晶间热电磁流动对枝晶演化的影响进行了研究,利用有限元软件COMSOL Multiphysics 对不同磁场强度下枝晶周围热电磁流动进行了模拟。计算区域人为的根据枝晶形状划分固相区和液相区。该枝晶的几何特征参照实验中观察到的柱状枝晶尖端区域。根据固相和液相区域给定不同的塞贝克系数和电导率。对各区域表面/界面施加无滑动边界条件,使熔体初始是静止的。模拟结果表明:热电磁流动的速度随着磁场的增大而增大,在6 T 附近达到最大值,同时三次枝晶臂两侧热电磁流动(Thermoelectromagnetic convection,TEMC)的大小不相等。实验结果与数值计算结果的对比表明,转轮状结构的发展与热电磁流动模式一致。这表明,三次枝晶形状的改变是枝晶尺度热电磁流动所致,不对称流场改变了局部过冷度,从而改变了三次枝晶形貌。
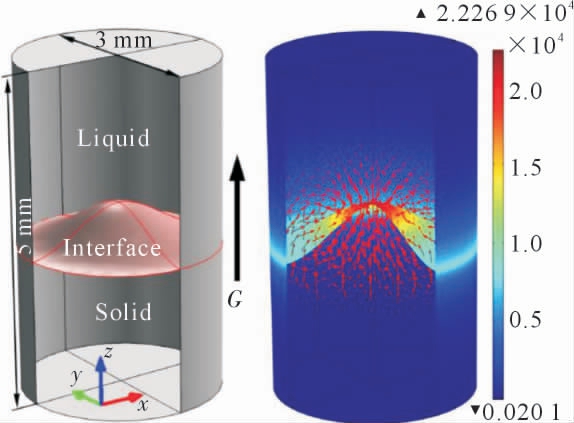
图5 固液界面示意图与固液界面周围的热电流[25]
Fig.5 Schematic diagram of solid liquid interface,thermo-electromagnetic current around the solid-liquid interface[25]
Bai 等[27]基于有限元/有限差分联合模拟方法研究了在电磁场作用下合金铸件定向凝固过程中凝固热、质量和动量传输。利用ANSYS 软件计算了相应的电磁场,通过转换文件,将有限元电磁场结果转换为差分格式,并耦合到温度、浓度、压力和液相流动速度等变量场中,采用有限差分进行求解。通过交变电磁场作用下γ(TiAl)型铸件定向凝固算例验证了该模型。Sampath 等[28]研究了在浮力、表面张力和电磁力共同作用下二元合金的定向凝固,提出了一种采用移动有限元技术的数值方法来模拟上述相变过程。将熔体模拟为布氏流体,用瞬态热方程和溶质运移方程同时求解瞬态Navier-Stokes 方程。采用Stefan 条件的保能弱形式数值确定了推进固液界面的位置。该文将不可压缩流体流动模拟的标准SUPG/PSPG 方法扩展到浮力、表面张力和电磁力共同驱动的流动,研究了稀锗合金(dilute germaniu alloy)水平开口船形定向凝固的参考问题。通过改变Bond 数,研究了热毛细对流和浮力驱动对流对凝固过程的相对影响。热毛细对流对固液界面形状和溶质偏析等凝固参数有显著影响,特别是在低重力条件下。随后研究了外加磁场对正常重力环境和减重环境下参考凝固问题的影响。结果表明,适当的强磁场可显著抑制熔体流动,改善溶质偏析模式。通过独立改变外加磁场的方向和大小,研究了外加磁场对凝固过程的相对影响。
1.4 焊接与增材制造过程模拟
焊接与增材制造过程是跨越较大时空尺度的过程,最大到零件尺度的热与应力分布,再到宏观熔池尺度的流动与传热,小到微介观尺度的枝晶生长,都会对最终产品性能有影响。本小节主要讨论电磁场下熔池尺度物理过程的模拟。
Bachmann 等[29]利 用COMSOL Multiphysics 有限元软件,对焊接过程中焊接熔池的变化进行了建模。根据不同激光穿透深度下材料的温度特性,求解了两种激光穿透深度下的三维传热、相变流体动力学和电磁场偏微分方程。用多孔介质形态的Carmen-Kozeny方程模拟凝固过程。通过增加达西源项的方式处理液固两相,并使用标准k-ε 模型的考虑湍流。Gatzen等[30]研究了在铝合金激光焊接中,磁场对焊缝形状,以及对熔池中硅分布的影响。利用CFX5.1 求解器,对外加磁场下铝激光焊接的流场进行了数值模拟。为了考虑熔池与保护气体之间的界面演化,采用体积分数法(VOF)来跟踪自由表面。结果表明,同轴施加静磁场会影响熔体的流动方向,作用机制可描述为一种非均匀电磁制动作用。于群等[31]采用有限元和有限体积法,对交变磁场作用下激光增材制造Ni45 合金过程进行了磁-热-流耦合数值分析。其中电磁部分通过有限元求解麦克斯韦方程组实现,流动传热部分通过有限体积法求解N-S 方程组实现。计算结果表明,外加磁场增强了由表面张力梯度和浮力耦合产生的强制性环流;随着磁场强度的增大,激光熔池的对流传热逐渐增强,这使得激光熔池的温度梯度逐渐减小,凝固速率逐渐增大;受此影响,合金成形体的凝固组织逐渐细化,硬度和摩擦磨损性能提高。Zhu 等[32]通过实验和多尺度数值模拟,针对静磁场对Inconel 625 高温合金选区熔化增材制造的影响进行了全面研究。利用商业有限元软件COMSOL Multiphysics 对SLM 过程熔池和枝晶间的热电磁力/流动分别进行了模拟(图6),模拟出的熔池尺寸与实验结果进行了验证。在洛伦兹力的影响下,熔池尺寸、流场、温度场没有明显变化。枝晶间模拟方面,利用实验观测的枝晶结构建立了枝晶数值模拟的几何形状,改变激光参数和磁场条件来研究其对热电磁力/流动的影响。模拟结果表明,施加磁场对枝晶生长的影响主要是固液界面上的热电磁力,而不是熔池内的洛伦兹力。在固液界面处热电流与热电磁力最大,从而影响枝晶的形貌,促进了柱状晶向等轴转变,这与0.1 T 磁场下的实验结果一致。
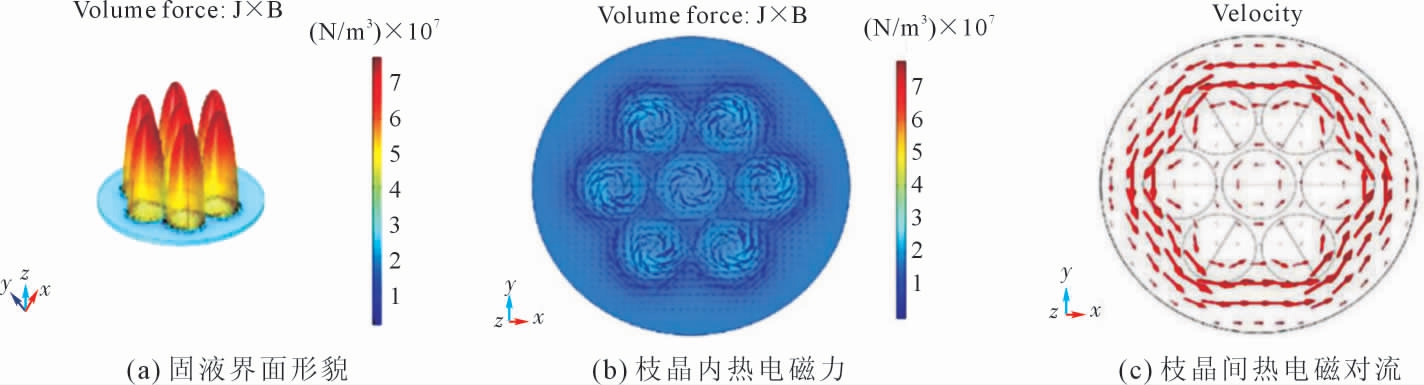
图6 模型中使用的固液界面形貌、枝晶内的热电磁力、枝晶间的热电磁对流[32]
Fig.6 Solid-liquid interface morphology used in the model,thermoelectric magnetic force in dendrites,thermoelectromagnetic convection between dendrites[32]
2 电磁冶金介观模拟(Mesoscopic simulation)
电磁冶金在宏观尺度的模拟已经发展了数十年的时间,算法相对成熟,通过对流体计算商业软件进行简单的二次开发即可完成绝大多数宏观尺度的模拟任务。然而仅通过宏观尺度模拟难以对合金凝固组织、微观偏析等进行全面分析,因此有必要进一步对凝固过程进行微观介观尺度的模拟。小尺度凝固模拟方法虽已发展四十余年,目前众多方法分支共同发展,大部分尚未形成商业化软件。本小节对近年来小尺度凝固模拟方法进行对比总结,并讨论各模型发展目前面临的问题。
2.1 晶体生长模拟
近年来,金属凝固组织计算方法一直在发展,而最直接方法就是模拟金属枝晶生长的过程。元胞自动机cellular automata(CA)法最早由冯诺伊曼在1950 年代提出,1980 年代开始应用于凝固过程模拟[33]。这一类CA 法基于尖锐界面方程组[34]。Stefanescu 等[35-36]通过改进CA 法的临胞捕获规则以降低网格各向异性的影响,该模型可以更真实的模拟0°和45°取向的枝晶。Zhu 等[37]进一步改进了他们CA 法的临胞捕获规则,使得该模型可以在均匀正方形网格内计算任意取向的枝晶生长过程,并后续扩展到三维空间[38]。引入高度函数法可以进一步消除网格各向异性[39],但由网格引起的各向异性依然存在。相场法建立在Ginzburg-Landau理论基础上,通过建立自由能/熵泛函来求解界面演化。Kobayashi[40]将相场法应用于二维枝晶生长模拟,方法表现出很低的网格各向异性。Karma 等把薄界面分析引入纯物质[41-42]以及合金[43-44]相场模型,使定量计算成为可能(图7)[45]。焓方法早期用于宏观凝固模拟[46-47],近年也被用于枝晶生长模拟[48]。Voller[49]通过引入尖锐界面方程组,将其扩展到二元合金体系。Voller 的焓方法引入溶势,溶势场被构造为在固液界面处平滑,无需在方程中单独加入溶质排出项。焓方法可比相场法应用到更大的尺度,但网格各向异性比相场大。

图7 基于相场法模拟枝晶生长[45]
Fig.7 Dendrite growth simulation via phase field method[45]
通过模拟晶粒生长也可以计算出金属凝固组织。在晶粒生长模拟的计算过程中枝晶的分支会被忽略,通过计算枝晶包络线的方式计算晶粒生长(图8[50])。晶界和晶粒取向的分布被作为研究对象,例如晶粒之间的竞争生长以及柱状-等轴转变(固液界面前沿发生大量形核时发生[51])。晶粒生长模拟中最常用的一种方法是由Rappaz[52]提出的一种元胞自动机方法(与上文中的另一类CA 法不同),使用偏行正方形临胞捕获规则来降低网格各向异性。Rap paz 引入连续形核模型算出液相中的形核概率与温度场的关系,使用Kurz-Giovanola-Trivedi (KGT)模型计算出枝晶尖端速度与温度场的关系[53-54]。为适应宏观尺度的计算,有限元被引入该CA 方法用以计算温度场,有限元算出的温度场信息(非结构化网格)以插值的方式导入正交网格的CA 模型中以实现温度场与形核生长过程的耦合[55],并在后续的工作中实现了三维化[56]。这类CA 方法在之后数年仍然持续发展[50,57-63]。相场法[64](与上文所述相场法不同)和蒙特卡洛法[65-66]也可以用于宏观晶粒生长的模拟,但是这两种方法相较于CA 法的在同尺度下对算力要求更高。

图8 基于元胞自动机法模拟晶粒生长[50]
Fig.8 Grain growth simulation via cellular automata method[50]
2.2 电磁场下晶体生长模拟
金属凝固过程不仅受到温度和溶质分布的影响,还会受到其他物理场(如流场、电场、磁场)的影响。在电磁冶金过程中,磁场下的熔体流动会切割磁感线并阻碍流体运动,同时外电场以及热电效应带来的电势差也会产生电流并作用在流体上,影响固液界面前沿溶质分布并最终影响生长过程,因此电磁冶金过程中的流动行为起到了关键的桥梁作用。要考虑各物理场对凝固过程的影响,就需要使用合适的算法计算出该物理场,并将之与凝固模拟方法进行耦合。
基于Karma 提出的相场模型[41],Beckermann[67-68]将流动过程与晶体生长过程进行耦合。其中流动部分使用一种隐式有限体积法求解,在固液界面处设置为无滑动边界条件。Sun 等[69]通过耦合相场法与晶格玻尔兹曼方法(LBM)来模拟流动中的晶体生长过程,在固液界面处使用反弹格式[70]来再现流动的无滑动边界条件,计算出的流场作用与相场方程中溶质输运的部分,以此实现晶体生长和流体流动的耦合。Rojas 等[71]同样使用了LBM 法与相场法耦合计算,但在处理LBM 流场时使用了外加的一个耗散力来保证固液界面的无滑动边界条件。此外,他们还加入了一组运动方程用于模拟晶粒在流体中的运动行为。Sakane 等[72]使用了多GPU 并行计算加速,用相场耦合LBM 计算了三维大尺度下的流动生长过程。在实际凝固过程中,枝晶周围流体可能还伴有气泡,这就涉及了固液气三相之间的交互作用。Zhang 等[73]开发了一种可以计算三种相(固液气)的相场法用于流体中的枝晶生长计算,其中固液界面以及气液界面使用相场方程描述,而液相内部以及气相内部的流动则分别耦合单相LBM 法进行模拟。Zhang 等[74]则使用不同方法处理固液气三相交互,其中枝晶生长(固液界面)部分使用了上文所述Zhu 等[37]提出的CA 法,而气相、液相及其相界面则基于shanchen-LBM 多相流模型[75]处理。
晶粒生长模拟同样可以与流场相耦合。Korner等[76-77]提出了一种尖锐界面LBM 方法,用以模拟气液界面以及液相的流动。与常规的两相流模型不同的是,这种模型将气体部分简化为饱和蒸汽压,这样处理巧妙地回避了两相流计算中两相密度差异过大带来的求解困难,同时这种模型还可以设定固液气三相的润湿角。之后他们将该模型与传热计算结合,模拟宏观熔凝过程(忽略枝晶与晶粒)[78],再将其与粉末堆积过程结合,再现了增材制造过程中的气孔形成[79-80]。他们进一步将计算晶粒生长的CA 法与尖锐界面LBM 方法耦合,计算晶粒在气液两相环境中的生长。其中CA 法与LBM 法是双向耦合的[81]。
电磁场下的金属凝固涉及到较多的物理过程。磁场下的流体流动会切割磁感线并阻碍流体运动,也就是磁阻尼作用。同时热电效应带来的电势差也会产生电流,该电流在磁场下受力也会作用在流体与固体上。根据电流与热输运的三个主要原则,热电效应可具体区分为:Peltier 效应、Thomson 效应和Seebeck 效应。在金属凝固过程中,Peltier 和Thomson 效应可以忽略不计[82]。因此,对电磁场下的凝固过程进行建模,Seebeck 效应是必须考虑的。根据Seebeck 效应,如果将具有不同热电系数的两相(如固体和液体)连接在一起,同时在两相之间施加温差,则两相之间存在电压差。在金属凝固过程中,正在生长中的枝晶时刻存在固液界面,此时若温度场不均匀,那么在固液界面周围时刻存在电势差。如图9 所示,假定此时的温场的温度梯度为竖直向上,图中心区域为枝晶,图外侧区域为液相,则界面内侧的电势逐渐升高,界面外侧电势逐渐降低,围绕固液界面将产生环形电流。而此时若在外部施加磁场,那么在液体内的这部分电流将受力产生流动,也就是热电磁流动。因此,磁场下金属凝固时,枝晶周围的流体受到两种作用,分别是流体本身切割磁感线阻碍流体流动的磁阻尼作用,和热电流在磁场下受力促进流体流动的热电磁流作用。这两种作用共同影响枝晶周围的流体流动,使之进一步影响传热与传质,并最终影响枝晶生长乃至金属凝固组织。
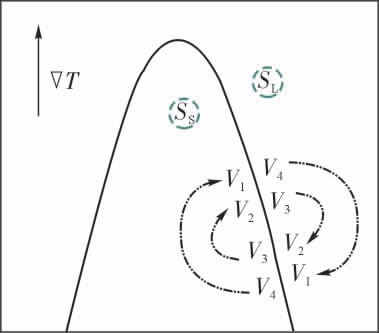
图9 热电磁流原理图
Fig.9 Schematic principle of thermoelectromagnetic flow
Kao 等[83-84]通过焓方法[49]与LBM 方法耦合计算对流中的枝晶生长,同时建立电势场,将磁阻尼以及固液界面处热电效应对电势的影响引入电势方程(6)。根据求解出的电势算出电流,将该电流对流动的作用力作为源项加入流动方程(7)中。
式(6)中,J 为电流,σ 为电导率,E 为电场强度,u 为流速,B 为磁场强度,S 为Seebeck 系数,∇T 为温度梯度。式(7)中ρ 为流体密度,t 为时间,∇p 为压力梯度,μ 为黏度。
Cao 等[85]使用相场法耦合LBM 的计算策略计算了磁场下晶体在流体中的生长过程,使用相场法替代焓方法计算枝晶生长(图10)。他们求解电势时,将固相液相以及界面分为了三个区域。如式(8~11)所示:
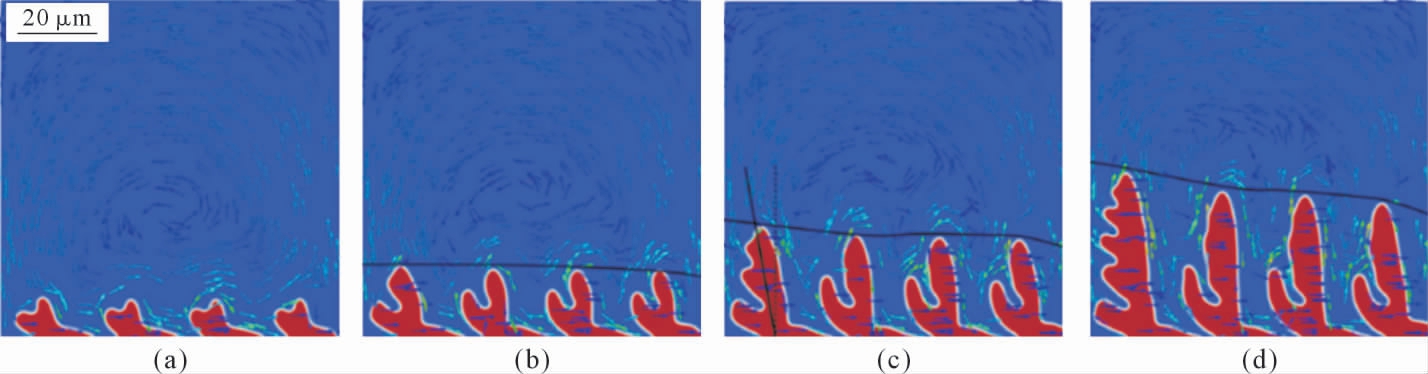
图10 横向静磁场作用下的枝晶生长[85]
Fig.10 Dendritic growth under transverse static magnetic field[85]

式中,V 为电势;Vint 为固液界面处电势。
这个计算区域内电势V 分布满足公式(8)(与公式(6)等价),但为实际求解时方便,在液相内区域使用公式(9),在固相内区域使用公式(10),在固液界面处使用公式(11)生成边界条件将固相和液相两个区域完全分隔开。由于电势方程计算边界处都是第二类边界条件,相对于直接使用公式(6)或者公式(8)求解电势场,将计算区域按照固液划分开在区域内部引入了第一类边界条件,不需要人为加入参考点,提高了计算求解的鲁棒性。Rasheed 等[86]将相场法与流动方程耦合求解磁场下的枝晶生长过程。他们的电流方程(12)除了考虑到电势梯度外,还将流体本身的流动考虑到总电流中。
式(12)中ρe 为流体中的电荷密度。但是他们的模型未考虑磁场下的热电效应。
上述这些多物理场耦合的模型中,枝晶生长部分(基于相场、焓或CA 法)一般用有限体积法或者显式有限差分法进行离散,而流动则多基于LBM方法,电磁则基于隐式差分,在离散上并不统一。Guo 等[87]使用一种并行多重网格法求解了流动中枝晶生长的过程,其中流动方程与描述枝晶生长的方程都是使用有限差分离散的。其后他们[88-89]使用并行自适应网格(Para-AMR)耦合相场与LBM,同样计算流动中的生长行为。Zhu 等[90]使用有限元求解了流动中纯物质枝晶生长的过程,其中生长部分使用自适应有限元求解相场方程,而流动部分则使用基于有限元的fractional-step projection 方法直接求解,整体的离散方法是一致的。Cartalade 等[91-92]发现相场方程的形式十分接近对流扩散方程(ADE),于是提出一种各向异性LBM 方法来直接求解描述枝晶生长的相场方程,而且该方法的网格各向异性非常低。Sun 等[93]基于Cartalade 的各向异性LBM 模型,耦合了流动过程的计算。流动部分也是用LBM 进行求解,因此这种模型处理枝晶生长与流动部分的离散方法也是一致的。之后Sun 等[94]将磁场也引入了流动-生长模型以计算不同磁场强度下枝晶生长的过程(图11)。其中晶体生长、流动、磁场全部都是使用LBM 方法求解,使用双松弛时间来分别处理磁场与流场,模型中没有包含磁场下的热电效应。
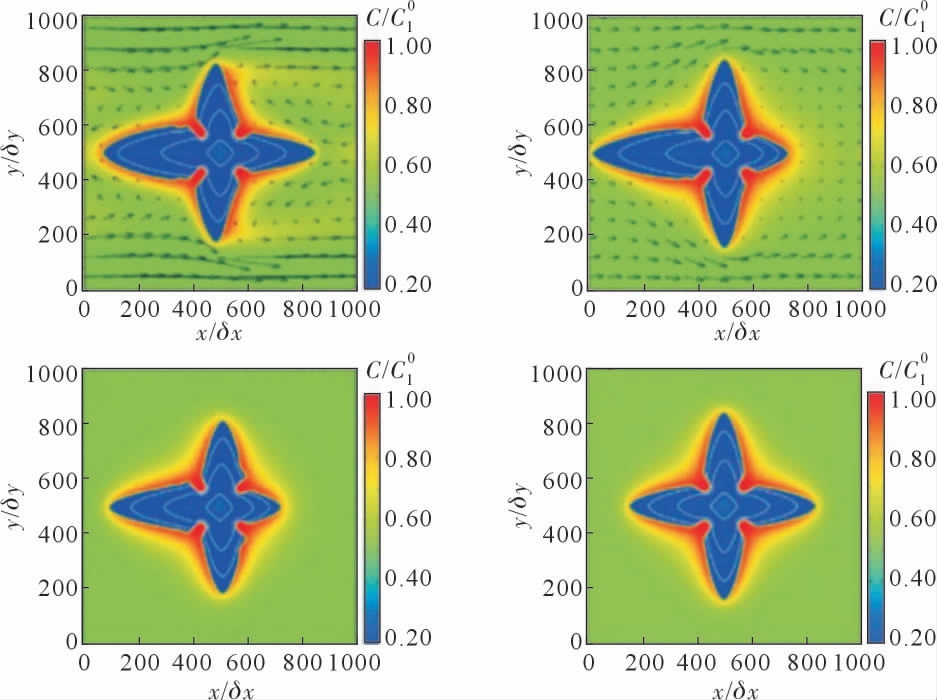
图11 不同磁场强度下流体中的枝晶生长[94]
Fig.11 Dendrite growth in fluid under different magnetic field intensities[94]
如本小节所述,在微观、介观尺度,有大量工作计算了磁场下金属凝固时宏观固液界面生长以及熔体流动,但受到计算机硬件以及模型本身的性质,难以向更大尺度扩展,也就更难与实际电磁冶金工程问题相结合。对于跨大时空尺度的情况,多尺度建模是一种十分便利的选择[95-97],但是将物理问题人为的分尺度谈论会带来一些应用难题(比如单晶增材制造等跨尺度过程)。因此,扩展现有微观、介观模拟方法的应用尺度,仍是电磁冶金过程模拟未来发展绕不开的问题。
4 结论与展望
经过几十年的发展,电磁冶金过程的大尺度模拟算法已十分成熟,在电磁、传热、传质、流动、凝固计算方面都可以借助商业软件完成。然而,大尺度凝固模型难以计算小尺度下的凝固组织形态、微观偏析等过程。电磁场下小尺度凝固模型研究得到了进一步发展,但目前仍未形成成熟的商业软件。在晶粒生长的尺度,元胞自动机法具有最高的计算效率,对于只针对晶粒生长的研究而言是最佳的选择。在枝晶生长尺度上的模拟方法中,相场法的物理基础最强,但计算时适用的时空尺度则最受限制。本文提到的多尺度模型可以一定程度上扩展小尺度方法的应用,但是由于实际冶金过程十分复杂,多尺度模型也有其局限性。
除多尺度模型外,一种处理方式是将相场方程以及流动全部使用LBM 法求解,利用LBM 易于大规模并行的特性,使用硬件加速扩大相场法的应用尺度。但是由于LBM 方法的显式特性,其求解时间步不能跨越太大,因此在时间尺度上依然受限,也同时造成了空间尺度上的限制。另一种处理方式是使用隐式方法求解相场方程,这样可以大大增加求解的时间步长,以此来显著增加相场法适用的时空尺度。隐式方法离散过程可通过特殊的离散处理以及稳定项的公式推导来保证系统的稳定性。此外,隐式求解相场方程需要组装一个很大的矩阵,对硬件内存和组装矩阵效率提出更高的要求。从发展前景来看,第二种处理方式(隐式求解)能够在跨长时间尺度的问题上充分利用高性能计算,同时进一步借助自适应方法,减少总的计算成本。也可以考虑matrix-free 方法减少内存和矩阵组装时间,提高计算效率。因此隐式求解最终适用的时空尺度更大,具有更大的应用前景,值得进一步投入资源发展。
电磁冶金过程的模拟还需要考虑多物理场的耦合计算,除了计算时需要的温度场、溶质场之外,主要考虑的场为流场与电磁场。正如上述,笔者更加倾向于使用隐式方法将所有方程隐式求解,这种处理方式会缓解物理问题时空尺度的限制,有更大的应用前景。另外,对于磁场下的凝固模拟,目前的模型都还不完善,例如磁场下的快速凝固模型(增材制造),以及枝晶在热电磁力的作用下的受力变形甚至折断的过程仍然未被实现,亟待进一步开发考虑全面物理过程的磁场下凝固模型。
[1]任忠鸣,雷作胜,李传军,等.电磁冶金技术研究新进展[J].金属学报,2020,56(4):583-600.
[2]ASAI S.Recent development and prospect of electromagnetic processing of materials[J].Science and Technology of Advanced Materials,2000,1(4):191-200.
[3]李喜,任忠鸣.静磁场下热电磁效应及其对凝固组织的影响[J].中国材料进展,2014,33(6):349-354.
[4]TOH T,TAKEUCHI E,HOJO M,et al.Electromagnetic control of initial solidification in continuous casting of steel by low frequency alternating magnetic field[J].ISIJ International,1997,37(11):1112-1119.
[5]KIM D S,KIM W S,CHO K H.Numerical simulation of the coupled turbulent flow and macroscopic solidification in continuous casting with electromagnetic brake[J].ISIJ International,2000,40(7): 670-676.
[6]LI B K,OKANE T,UMEDA T.Modeling of molten metal flow in a continuous casting process considering the effects of argon gas injection and static magnetic-field application[J].Metallurgical and Materials Transactions B,2000,31:1491-1503.
[7]YAMAZAKI M,NATSUME Y,HARADA H,et al.Numerical simulation of solidification structure formation during continuous casting in Fe-0.7mass%C alloy using cellular automaton method[J].ISIJ International,2006,46(6):903-908.
[8]SONG X P,CHENG S S,CHENG Z J.Mathematical modelling of billet casting with secondary cooling zone electromagnetic stirrer[J].Ironmaking&Steelmaking,2013,40(3):189-198.
[9]YANG B,DENG A,LI Y,et al.Numerical simulation of flow and solidification in continuous casting process with mold electromagnetic stirring[J].Journal of Iron and Steel Research International.2019,26(3):219-229.
[10]WANG B,YANG Z G,ZHANG X F,et al.Analysis of the effects of electromagnetic stirring on solidification structure of bearing steel[J].Metalurgija,2015,54(2):327-330.
[11]SHVIDKIY E L,SOKUNOV B A,USKOV I A,et al.Simulation of continuous casting process with electromagnetic influence to the ingot liquid phase[C]//2016 IEEE NW Russia Young Researchers in Electrical and Electronic Engineering Conference (EIConRus-NW).New York:IEEE Xplore,2016.685-688.
[12]REN B Z,CHEN D F,WANG H D,et al.Numerical simulation of fluid flow and solidification in bloom continuous casting mould with electromagnetic stirring[J].Ironmaking&Steelmaking.2015,42(6):401-408.
[13]YIN Y B,ZHANG J M,LEI S W,et al.Numerical study on the capture of large inclusion in slab continuous casting with the effect of in-mold electromagnetic stirring[J].ISIJ International.2017,57:2165-2174.
[14]FANG Q,NI H W,ZHANG H,et al.The effects of a submerged entry nozzle on flow and initial solidification in a continuous casting bloom mold with electromagnetic stirring[J].Metals-Open Access Metallurgy Journal,2017,7(4):146.
[15]GUAN R,JI C,ZHU M Y.Modeling the effect of combined Electromagnetic stirring modes on macrosegregation in continuous casting blooms[J].Metallurgical and Materials Transactions B,2020,51:1137-1153.
[16]周然,樊亚夫,邓康,等.电磁制动下板坯连铸结晶器内金属流场三维模拟的基本流态与主流场分析[J].上海大学学报(自然科学版),2016,22:701-709.
[17]KAGEYAMA R,EVANS J W.Development of a three dimensional mathematical model of the electromagnetic casting of steel[J].ISIJ International,2002,42(2):163-170.
[18]CHAUDHARY R,VANKA S P,THOMAS B G.Direct numerical simulations of magnetic field effects on turbulent flow in a square duct[J].Physics of Fluids,2010,22(7):075102.
[19]BERM DEZA,MUÑIZ M C,SALGADO P.Asymptotic approximation and numerical simulation of electromagnetic casting[J].Metallurgical and Materials Transactions B-Process Metallurgy and Materials Processing Science,2003,34:83-91.
DEZA,MUÑIZ M C,SALGADO P.Asymptotic approximation and numerical simulation of electromagnetic casting[J].Metallurgical and Materials Transactions B-Process Metallurgy and Materials Processing Science,2003,34:83-91.
[20]DUAN W C,YIN S Q,LIU W H,et al.Numerical study of flow and heat transfer behaviors during direct-chill casting of large-size magnesium alloy billet under pulsed magnetic field[J].International Journal of Numerical Methods for Heat&Fluid Flow,2021,31:829-857.
[21]DREZET J M,RAPPAZ M,KRA¨HENBU¨HL Y.Thermomechanical effects during direct chill and electromagnetic casting of aluminum alloys.part II: numerical simulation[M].Warrendale,PA:TMS,1995.
[22]HATIC'V,MAVRICˇB,SˇARLER B.Simulation of macrosegregation in low-frequency electromagnetic casting by a meshless method[C]//COUPLED VIII: proceedings of the VIII International Conference on Computational Methods for Coupled Prob lems in Science and Engineering.Barcelona: CIMNE,2019,118-127.
[23]SHA M H,WANG T M,BAI F D,et al.Simulation on solidification of an Al-Ni alloy under electromagnetic stirring[J].China Foundry,2012,9:258-262.
[24]LE Q C,GUO S J,ZHAO Z H,et al.Numerical simulation of electromagnetic DC casting of magnesium alloys[J].Journal of Materials Processing Technology,2007,183(2-3):194-201.[25]WANG J,FAUTRELLE Y,NGUYEN-THI H,et al.Thermoelectric magnetohydrodynamic flows and their induced change of solid-liquid interface shape in static magnetic field-assisted directional solidification[J].Metallurgical and Materials Transactions A,2016,47:1169-1179.
[26]ZHONG H,LI C J,REN Z M,et al.Effect of interdendritic thermoelectric magnetic convection on evolution of tertiary dendrite during directional solidification[J].Journal of Crystal Growth,2016,439:66-73.
[27]BAI Y F,XU D M,MAO L H,et al.FEM/FDM-joint simulation for transport phenomena in directionally solidifying shaped TiAl casting under electromagnetic field[J].ISIJ International,2004,44:1173-1179.
[28]SAMPATH R,ZABARAS N.Numerical study of convection in the directional solidification of a binary alloy driven by the combined action of buoyancy,surface tension,and electromagnetic forces[J].Journal of Computational Physics,2001,168(2):384-411.
[29]BACHMANN M,AVILOV V,GUMENYUK A,et al.Numerical assessment and experimental verification of the influence of the hartmann effect in laser beam welding processes by steady magnetic fields[J].International Journal of Thermal Sciences,2016,101:24-34.
[30]GATZEN M,TANG Z.CFD-based model for melt flow in laser beam welding of aluminium with coaxial magnetic field[J].Physics Procedia,2010,5:317-326.
[31]于群,王存山.电磁搅拌辅助Ni45 合金的激光增材制造[J].中国激光,2018,45(4):0402003.
[32]ZHU W L,YU S,CHEN C Y,et al.Effects of static magnetic field on the microstructure of selective laser melted inconel 625 superalloy:numerical and experiment investigations[J].Metals,2021,11(11):1846.
[33]REUTHER K,RETTENMAYR M.Perspectives for cellular automata for the simulation of dendritic solidification-A review[J].Computational Materials Science,2014,95:213-220.
[34]SASIKUMAR R,SREENIVASAN R.Two-dimensional simulation of dendrite morphology[J].Acta Metallurgica et Materialia,1994,42(7):2381-2386.
[35]BELTRAN-SANCHEZ L,STEFANESCU D M.A quantitative dendrite growth model and analysis of stability concepts[J].Metallurgical and Materials Transactions A,2004,35:2471-2485.
[36]BELTRAN-SANCHEZ L,STEFANESCU D M.Growth of solutal dendrites:A cellular automaton model and its quantitative capabilities [J].Metallurgical and Materials Transactions A,2003,34:367-382.
[37]ZHU M F,STEFANESCU D M.Virtual front tracking model for the quantitative modeling of dendritic growth in solidification of alloys[J].Acta Materialia,2007,55(5):1741-1755.
[38]PAN S Y,ZHU M F.A three-dimensional sharp interface model for the quantitative simulation of solutal dendritic growth[J].Acta Materialia,2010,58(1):340-352.
[39]WEI L,CAO Y Q,LIN X,et al.Quantitative cellular automaton model and simulations of dendritic and anomalous eutectic growth[J].Computational Materials Science,2019,156:157-166.
[40]KOBAYASHI R.Modeling and numerical simulations of dendritic crystal growth[J].Physica D:Nonlinear Phenomena,1993,63(3-4):410-423.
[41]KARMA A,RAPPEL W J.Phase-field method for computationally efficient modeling of solidification with arbitrary interface kinetics[J].Physical Review E,1996,53(4):R3017-R3020.
[42]KARMA A,RAPPEL W J.Quantitative phase-field modeling of dendritic growth in two and three dimensions[J].Physical Review E,1998,57:4323-4349.
[43]KARMA A.Phase-field formulation for quantitative modeling of alloy solidification[J].Physical Review Letters,2001,87:115701.
[44]ECHEBARRIA B,FOLCH R,KARMA A,et al.Quantitative phase-field model of alloy solidification[J].Physical Review E,2004,70:061604.
[45]TOURRET D,KARMA A.Growth competition of columnar dendritic grains: A phase-field study[J].Acta Materialia,2015,82:64-83.
[46]ROSE M E.An implicit enthalpy scheme for one-phase Stefan problems[J].Journal of Scientific Computing,1990,5:169-185.
[47]KRABBENHOFT K,DAMKILDE L,NAZEM M.An implicit mixed enthalpy-temperature method for phase-change problems[J].Heat and Mass Transfer,2007,43:233-241.
[48]PAL D,BHATTACHARYA J,DUTTA P,et al.An enthalpy model for simulation of dendritic growth[J].Numerical Heat Transfer,Part B:Fundamentals,2006,50(1):59-78.
[49]VOLLER V R.An enthalpy method for modeling dendritic growth in a binary alloy[J].International Journal of Heat and Mass Transfer,2008,51(3-4):823-834.
[50]ZINOVIEVA O,ZINOVIEV A,PLOSHIKHIN V,et al.A solution to the problem of the mesh anisotropy in cellular automata simulations of grain growth[J].Computational Materials Science,2015,108:168-176.
[51]HUNT J D.Steady state columnar and equiaxed growth of dendrites and eutectic[J].MaterialsScience and Engineering,1984,65(1):75-83.
[52]RAPPAZ M,GANDIN C A.Probabilistic modeling of microstructure formation in solidification processes[J].Acta Metallurgica et Materialia,1993,41(2):345-360.
[53]LIPTON J,GLICKSMAN M E,KURZ W.Dendritic growth into undercooled alloy metals[J].Materials Science and Engineering,1984,65(1):57-63.
[54]KURZ W,GIOVANOLA B,TRIVEDI R.Theory of microstructural development during rapid solidification[J].Acta Metallurgica,1986,34(5):823-830.
[55]GANDIN C A,RAPPAZ M.A coupled finite element-cellular automaton model for the prediction of dendritic grain structures in solidification processes[J].Acta Metallurgica et Materialia,1994,42(7):2233-2246.
[56]GANDIN C A,RAPPAZ M.A 3D Cellular Automaton algorithm forthe prediction of dendritic graingrowth[J].ActaMaterialia,1997,45(5):2187-2195.
[57]ZHAN X H,WEI Y H,DONG Z B.Cellular automaton simulation of grain growth with different orientation angles during solidification process[J].Journal of Materials Processing Technology,2008,208(1-3):1-8.
[58]LUO S,ZHU M Y.A two-dimensional model for the quantitative simulation of the dendritic growth with cellular automaton method[J].Computational Materials Science,2013,71:10-18.
[59]ZINOVIEV A,ZINOVIEVA O,PLOSHIKHIN V,et al.On the numerical simulation of the microstructural evolution induced by laser additive manufacturing of steel products[C]//AIP Conference Proceedings.New York:AIP Publishing,2016.040097.
[60]ZINOVIEV A,ZINOVIEVA O,PLOSHIKHIN V,et al.Evolution of grain structure during laser additive manufacturing.Simulation by a cellular automata method[J].Materials &Design,2016,106:321-329.
[61]ZINOVIEVA O,ZINOVIEV A,PLOSHIKHIN V.Three-dimensional modeling of the microstructure evolution during metal additive manufacturing[J].Computational MaterialsScience,2018,141:207-220.
[62]LIAN Y P,LIN S,YAN W T,et al.A parallelized three-dimensional cellular automaton model for grain growth during additive manufacturing[J].Computational Mechanics,2018,61:543-558.
[63]LIAN Y P,GAN Z T,YU C,et al.A cellular automaton finite volume method for microstructure evolution during additive manufacturing[J].Materials&Design,2019,169:107672.
[64]LU L X,SRIDHAR N,ZHANG Y W.Phase field simulation of powder bed-based additive manufacturing[J].Acta Materialia,2018,144:801-809.
[65]RODGERS T M,MADISON J D,TIKARE V,et al.Predicting mesoscale microstructural evolution in electron beam welding[J].JOM,2016,68:1419-1426.
[66]RODGERS T M,MADISON J D,TIKARE V.Simulation of metal additive manufacturing microstructures using kinetic monte carlo[J].Computational Materials Science,2017,135:78-89.
[67]BECKERMANN C,DIEPERS H J,STEINBACH I,et al.Modeling melt convection in phase-field simulations of solidification[J].Journal of Computational Physics,1999,154(2):468-496.
[68]DIEPERS H J,BECKERMANN C,STEINBACH I.Simulation of convection and ripening in a binary alloy mush using the phase-field method[J].Acta Materialia,1999,47(13):3663-3678.
[69]SUN D K,ZHU M F,PAN S Y,et al.Lattice Boltzmann modeling of dendritic growth in a forced melt convection[J].Acta Materialia,2009,57(6):1755-1767.
[70]MAIER R S,BERNARD R S,GRUNAU D W.Boundary conditions for the lattice Boltzmann method[J].Physics of Fluids,1996,8:1788-1801.
[71]ROJAS R,TAKAKI T,OHNO M.A phase-field-lattice Boltzmann method for modeling motion and growth of a dendrite for binary alloy solidification in the presence of melt convection[J].Journal of Computational Physics,2015,298:29-40.
[72]SAKANE S J,TAKAKI T,ROJAS R,et al.Multi-GPUs parallel computation of dendrite growth in forced convection using the phase-field-lattice Boltzmann model[J].Journal of Crystal Growth,2017,474:154-159.
[73]ZHANG A,DU J L,ZHANG X P,et al.Phase-field modeling of microstructure evolution in the presence of bubble during solidification[J].Metallurgical and Materials Transactions A,2020,51:1023-1037.
[74]ZHANG Q Y,SUN D K,PANG S Y,et al.Microporosity formation and dendrite growth during solidification of aluminum alloys:Modeling and experiment[J].InternationalJournalofHeatandMass Transfer,2020,146:118838.
[75]SHAN X W,CHEN H D.Lattice Boltzmann model for simulating flows with multiple phases and components[J].Physical Review E,1993,47:1815-1819.
[76]KO¨ RNER C,THIES M,HOFMANN T,et al.Lattice boltzmann model for free surface flow for modeling foaming[J].Journal of Statistical Physics,2005,121:179-196.
[77]ATTAR E,KO¨ RNER C.Lattice Boltzmann method for dynamic wetting problems[J].Journal ofColloid and Interface Science,2009,335(1):84-93.
[78]ATTAR E,KO¨RNER C.Lattice Boltzmann model for thermal free surface flows with liquid-solid phase transition[J].International Journal of Heat and Fluid Flow,2011,32(1):156-163.
[79]KO¨RNER C,ATTAR E,HEINL P.Mesoscopic simulation of selective beam melting processes[J].Journal of Materials Processing Technology,2011,211(6):978-987.
[80]AMMER R,MARKL M,LJUNGBLAD U,et al.Simulating fast electron beam melting with a parallel thermal free surface lattice Boltzmann method [J].Computers &Mathematics with Applications,2014,67(2):318-330.
[81]RAI A,MARKL M,KO¨RNER C.A coupled Cellular Automaton-Lattice Boltzmann model for grain structure simulation during additive manufacturing[J].Computational Materials Science,2016,124:37-48.
[82]LEHMANN P,MOREAU R,CAMEL D,et al.Modification of interdendritic convection in directional solidification by a uniform magnetic field[J].Acta Materialia,1998,46(11):4067-4079.
[83]KAO A,SHEVCHENKO N,ROSHCHUPINKA O,et al.The effects of natural,forced and thermoelectric magnetohydrodynamic convection during the solidification of thin sample alloys[C]//IOP Conference Series: Materials Science and Engineering.Bristol:IOP Publishing,2015.012018.
[84]KAO A,CAI B,LEE P D,et al.The effects of Thermoelectric Magnetohydrodynamics in directional solidification under a transverse magnetic field[J].Journal of Crystal Growth,2017,457:270-274.
[85]CAO L H,LIU D H,JIANG P,et al.Multi-physics simulation of dendritic growth in magnetic field assisted solidification[J].International Journal of Heat and Mass Transfer,2019,144:118673.
[86]RASHEED A,BELMILOUDI A.Mathematical modelling and numerical simulation of dendrite growth using phase-field method with a magnetic field effect[J].Communications in Computational Physics,2013,14(2):477-568.
[87]GUO Z,MI J,XIONG S,et al.Phase field study of the tip operating state of a freely growing dendrite against convection using a novel parallel multigrid approach[J].Journal of Computational Physics,2014,257:278-297.
[88]ZHANG X,KANG J,GUO Z,et al.Development of a Para-AMR algorithm for simulating dendrite growth under convection using a phase-field-lattice Boltzmann method[J].Computer Physics Communications,2018,223:18-27.
[89]ZHANG A,MENG S X,GUO Z P,et al.Dendritic growth under natural and forced convection in Al-Cu alloys: From equiaxed to columnar dendrites and from 2D to 3D phase-field Simulations[J].Metallurgical and Materials Transactions B,2019,50:1514-1526.
[90]ZHU C S,LEI P,XIAO R Z,et al.Phase-field modeling of dendriticgrowth under forced flow based on adaptive finite element method[J].Transactions of Nonferrous Metals Society of China,2015,25(1):241-248.
[91]CARTALADE A,YOUNSI A,PLAPP M.Lattice Boltzmann simulations of 3D crystal growth:Numerical schemes for a phase-field model with anti-trapping current[J].Computers &Mathematics with Applications,2016,71(9):1784-1798.
[92]YOUNSI A,CARTALADE A.On anisotropy function in crystal growth simulations using Lattice Boltzmann equation [J].Journal of Computational Physics,2016,325:1-21.
[93]SUN D K,XING H,DONG X L,et al.An anisotropic lattice Boltz-mann-Phase field scheme for numerical simulations of dendritic growth with melt convection[J].International Journal of Heat and Mass Transfer,2019,133:1240-1250.
[94]MAO S L,WANG X Z,SUN D K,et al.Numerical modeling of dendrite growth in a steady magnetic field using the two relaxation times lattice Boltzmann-Phase field model[J].Computational Materials Science,2022,204:111149.
[95]JIANG P,GAO S,GENG S N,et al.Multi-physics multi-scale simulation of the solidification process in the molten pool during laser welding of aluminum alloys[J].International Journal of Heat and Mass Transfer,2020,161:120316.
[96]XIAO W J,LI S M,WANG C S,et al.Multi-scale simulation of dendrite growth for direct energy deposition of nickel-based superalloys[J].Materials&Design,2019,164:107553.
[97]NIE P L,OJO O A,LI Z G.Numerical modeling of microstructure evolution during laser additive manufacturing of a nickel-based superalloy[J].Acta Materialia,2014,77:85-95.