在液态金属中,扩散是质量传输的主要形式[1-2]。它是发生在物质微粒(离子、原子和分子)间的热运动而产生的物质迁移现象。液态金属和半导体材料中的扩散在材料、冶金化学领域(如凝固、腐蚀和相变等研究)以及液体物理学中是一个常见的物理现象[3-5]。凝固过程中所涉及的偏析、枝晶臂间距和枝晶形貌演化等现象都与扩散密切相关。扩散系数作为描述熔体动力学行为的核心参数,其测量方法和理论研究一直是研究者们的关注热点。已有的研究表明,某些合金熔体扩散系数的改变会直接影响凝固组织的成分分布和微观形貌,进而最终决定材料性能。此外,金属熔体的扩散系数也是模拟微观组织演变的必要参数之一,还可作为检验和校准分子动力学模拟结果的基准[6-10]。
因此,准确测量液态金属的扩散系数有助于人们了解金属熔体的原子结构和原子迁移的物理本质,为液态金属原子的扩散机制和物理模型的建立以及后续的材料设计等诸多研究提供实验依据[10]。然而,液态金属中溶质的扩散系数大小通常为10-9m2/s。因此,流动所引起的溶质交换会对测量结果产生极大影响。由于温度梯度、真空度等影响因素,液态金属在重力和高温环境下会不可避免地存在多种类型的流动,如浮力对流和Marangoni(马兰戈尼) 流动[6]。其中浮力对流是由于扩散试样中两种金属的密度差异,导致地面环境下金属熔体状态不稳定产生的熔体对流。Marangoni 对流则是由温度梯度、成分差或金属熔体与测量装置内壁之间存在界面张力梯度差引起的熔体对流。
地面上液态金属扩散系数测量技术例如长管技术[11-17]、毛细管-熔池法[18-20]、剪切单元技术[21-23]、滑动剪切单元技术[2]等都无法从根本上抑制重力引起的对流。然而受到实验成本和空间技术条件的限制,空间微重力环境下的金属熔体扩散研究并未广泛开展[24]。且从已有的实验结果可以看出,测量得到的扩散系数依旧受到了Marangoni 流动的影响。
为此,研究者们在测量过程中施加强静磁场,希望借助磁制动效应抑制熔体对流创造一个纯扩散测量环境[25-26]。由于国内外所有强磁体的口径较小,比如超导磁体口径常在100~200 mm 范围内,而对于超强电阻磁体(Bitter 磁体),其口径也仅为50 mm。除去磁体口径尺寸限制之外,测量装置的复杂、等温扩散过程中样品的氧化、熔体中Marangoni流动等问题依然是强静磁场下合金熔体扩散行为研究的难点。因此,亟需设计一种适用于小口径超高强Bitter 磁体发生器中的液态金属扩散系数的测量装置,并利用该测量装置在不同磁场环境中进行金属熔体互扩散系数的测量实验,建立强静磁场下金属的液态扩散理论体系,以期利用强静磁场提供纯扩散测量环境来更为准确地测量合金熔体扩散系数。
本文作者综述了合金熔体扩散系数的测量方法以及测量环境对合金熔体扩散系数的影响,并指出强静磁场在合金熔体扩散系数测量中的作用。设计了一种可用于强静磁场下合金熔体扩散系数测量的装置,并探究了0~22 T 强静磁场对合金熔体扩散系数的影响。
1 合金熔体互扩散系数的测量方法
互扩散也称为化学扩散,是指发生在含有两种或两种以上的扩散组元的体系中各组元的扩散过程。表象上这些组元由浓度梯度驱动扩散,但本质上是由化学势梯度作为扩散的驱动力,产生沿浓度梯度方向上的净扩散通量,从而使宏观浓度分布不均匀的系统趋向均匀,降低整个体系的自由能。互扩散系数不仅体现了该体系中组元间相互扩散的能力,还与扩散机理密切相关。其中,原子的扩散过程通常满足菲克第二定律,即:
式中,C 为组元的物质的量浓度;t 为等温扩散时间;x 为沿扩散偶长度方向上的距离;D 为组元的互扩散系数。现有金属熔体互扩散系数的测量装置主要分为以下3 种:长毛细管装置[27]、毛细管-熔池装置[18-20]和剪切单元装置[28]。下文将详细介绍利用上述3 种测量装置进行扩散系数的测量方法以及其他测量技术。
1.1 长毛细管技术
长毛细管技术是将两个直径为0.5~2.0 mm[29]的相同尺寸的不同固态金属分别放置于长毛细管的上下两端,如图1 所示。再将放置好的试样加热到目标扩散温度并进行一段时间保温,然后将试样快速冷却至室温,对凝固试样进行成分检测,获得成分-距离分布图,最后根据菲克第二定律,结合初始条件和边界条件拟合计算得到互扩散系数。
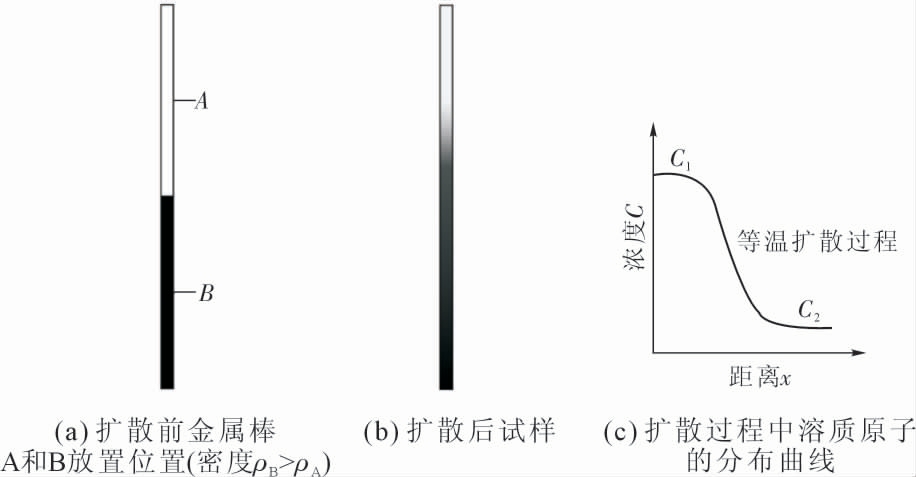
图1 长毛细管技术示意图
Fig.1 Schematic diagram of long capillary technique
毛细管直径的大小与金属熔体扩散过程中熔体对流直接相关,减小毛细管直径能一定程度上抑制熔体对流。但直径过小产生的壁效应[30]会抑制熔体扩散过程进而影响测量结果。其次金属棒放置的顺序为密度较大的金属棒在下,密度较小的金属棒在上,这也能在一定程度上减少重力对流对测量结果的影响。为了避免扩散样品被氧化和毛细管中产生气泡引起额外的Marangoni 对流,扩散实验需要在负压条件下进行。试样升温以及降温过程中金属棒A 和B 一直紧密接触,因此测量得到的互扩散系数会受到升温以及降温过程的影响而大于实际值。且样品冷却过程中的凝固收缩以及凝固偏析现象也会对后续成分测量造成影响。针对上述情况,可在一定程度上缩小实验样品的直径,且使实验样品的长度远大于样品直径。其次为减小升温以及降温过程中的影响,可以加大升温速率和延长等温扩散时间。
1.2 毛细管-熔池技术
毛细管-熔池技术是将装有一种液态金属的毛细管在目标扩散温度下浸入装有一种液态金属的大熔池内(如图2 所示),保温一段时间后,将毛细管从熔池内取出,迅速降温至试样完全凝固。沿试样不同高度测出溶质金属的浓度分布,并拟合计算得出互扩散系数值。事实上,上述的长毛细管技术和毛细管-熔池技术都无法完全避免在到达目标温度之前的升温过程以及后续降温过程中的原子扩散问题,且冷却过程中的凝固收缩问题也不能得到有效解决。与长毛细管技术相比,该方法有效地避免了升温过程中原子的扩散过程,而且对外界造成的扰动相对不灵敏。但是大熔池中会产生较大的熔体对流,且会一定程度延伸到毛细管中,对实验结果造成一定的误差。
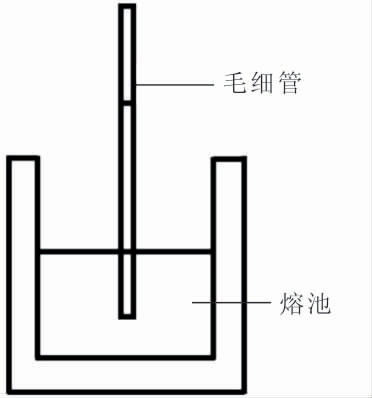
图2 毛细管-熔池装置示意图
Fig.2 Schematic diagram of capillary-melt pool device
1.3 剪切单元技术
该实验装置是由相同形状的转盘同轴罗列而成[2,31],且在偏离转盘中心处有一条扩散通道,如下图3 所示。在升温之前将两个不同成分的金属样品分别放置,升温到目标温度(扩散金属熔点以上)之前,两种成分不同的金属样品已经完全熔化时,将系统重新抽真空。在到达扩散温度下转动转盘形成扩散偶,扩散一段时间后,再转动转盘将金属熔体扩散偶分割成多层小薄片(20~30 层),待每层试样完全凝固之后,沿着长度方向对每个薄片试样进行成分分析,得到该扩散偶的溶质浓度分布,拟合计算得出互扩散系数值。扩散样品被分为多层小薄片在一定程度上避免了成分偏析对互扩散系数造成的影响。
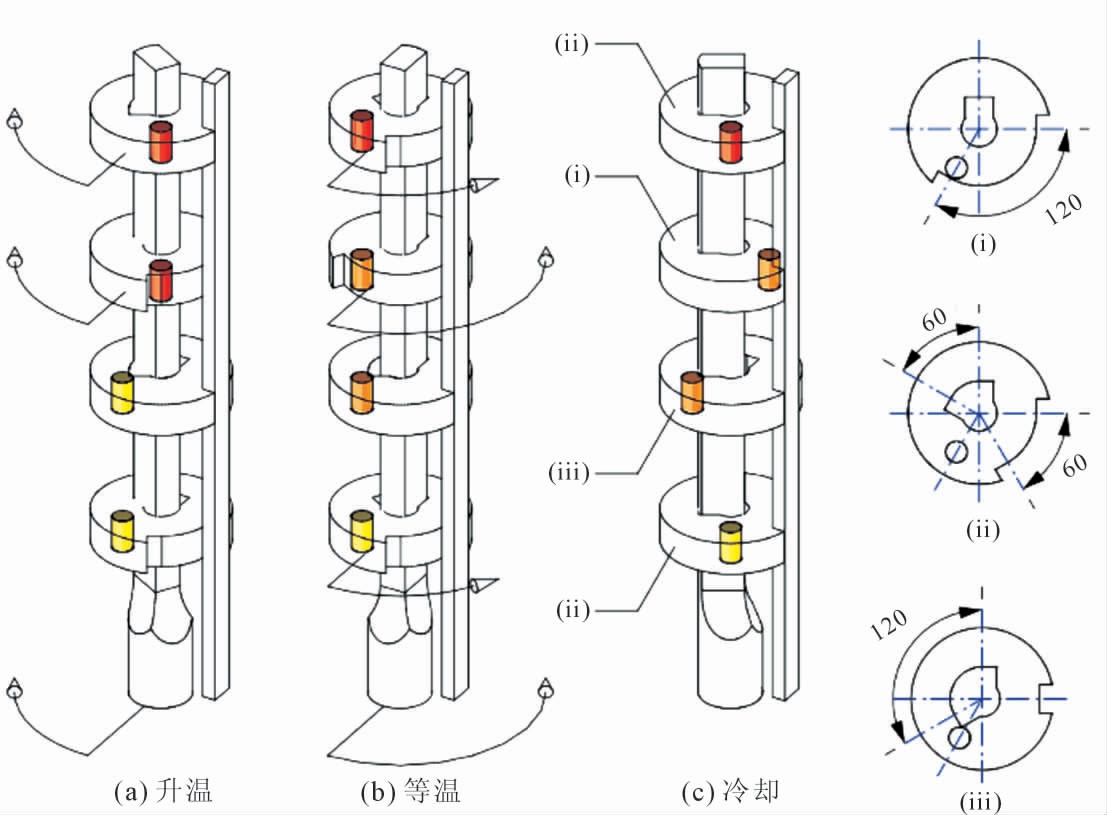
图3 剪切单元装置示意图[31]
Fig.3 Schematic diagram of shearing cell technique[31]
剪切单元技术法能够有效消除升温以及降温过程中额外的原子扩散过程的影响,包括降温过程中的热膨胀、凝固收缩等问题。但由于设备复杂,该测量方法对加热、等温扩散以及降温过程中的各部分操作要求非常细致协调,且设备本身的精密加工具有一定难度,扩散偶的对中问题很难保证。在扩散开始以及扩散结束阶段,转盘转动会对液态金属产生搅拌作用,增加熔体对流,也会对后续测量造成影响。
1.4 滑动剪切技术
虽然剪切单元技术能避免升温和降温过程的原子扩散对测量结果的影响,但是这种技术结构过于复杂,装置加工与实验操作都十分困难。因此,耿永亮等[2,32]设计了滑动剪切技术用于测量液态金属互扩散系数,如图4 所示。真空腔体侧壁上安装有一个可活动的手动推杆,可精准推动扩散工作台的滑动块单元。为了避免升温过程中的影响,首先将两段扩散样分离,加热至扩散温度(高于试样熔点)并保温一段时间后,推动手动推杆使两段扩散试样对接,待扩散时间结束,通入高纯氮气加快冷却试样,获得扩散偶试样。该技术能避免升温过程中对实验结果的影响,且操作简单,但由于降温过程中通入氮气,冷却时间较长,测量得到的互扩散系数依旧存在降温过程中的影响。且液态样品与试管壁之间的自由表面引起的Marangoni 对流也会对实验结果造成影响。

图4 滑动剪切技术的工作原理图[32]
Fig.4 Schematic diagram of sliding cell technology[32]
1.5 X 射线成像技术
随着实验技术的发展,X 射线成像技术[1]以及滑动剪切技术[2]逐渐被用于金属熔体的互扩散系数测量实验中。X射线成像技术(X-ray radiography,XRR)是基于长毛细管技术,增加了成像系统以及X-射线光源实现了金属熔体互扩散系数的原位测量,是目前较为先进的原位测量技术,成像过程如图5 所示。该技术通过X-射线光源发出的射线照射样品台,成像探测器上会得到图像,该图像与不同含量的元素相对应,结合灰度值与已知合金标准样,将图像转换为不同时刻对应的浓度变化曲线。若存在额外的物质传输,图像中会出现偏差,XRR 能监测扩散试样升温、等温扩散以及降温整个过程的原子扩散行为。此外XRR 能实时反应试样的状态,有无气泡生成,因此能大大提高互扩散系数的测量精度。
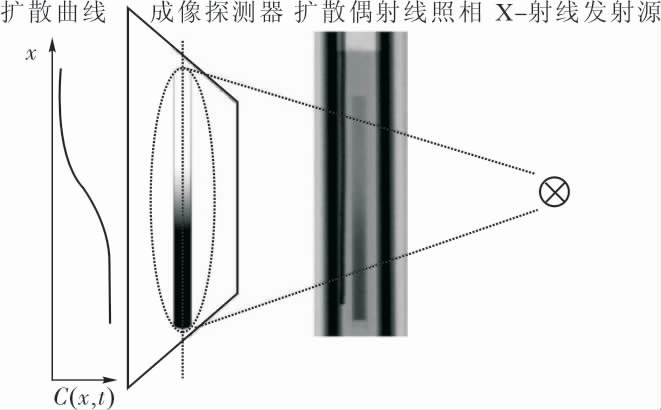
图5 X 射线成像技术测量金属熔体互扩散系数示意图[33]
Fig.5 Schematic diagram of measuring interdiffusion coefficient of metal melt by X-ray radiography[33]
1.6 重力辅助自动对接技术
为了避免扩散偶界面的氧化,并简化实验装置以适应有限体积测量环境。本课题组设计了重力辅助自动对接装置[34-35],如图6 所示。重力辅助自动对接装置主要由四部分组成:石英管、配重块、石墨坩埚(可替换为氮化硼坩埚等其他材质坩埚)和金属棒。为了减小重力产生的对流作用对扩散的影响,密度较大的合金棒试样放于底部石墨坩埚Ⅰ内,密度较小的合金棒试样放于上端石墨坩埚Ⅲ内,将黄铜棒放置在石墨坩埚Ⅲ上端,对石英管进行密封真空处理。扩散偶形成示意图如图6(b)所示。当温度超过两合金熔点时,上部的合金将在重力的作用下与下方合金形成扩散偶,多余的合金液体将被排入到周边的空腔中。该装置避免了扩散偶界面处的氧化问题且结构简单易于操作,适用于小口径磁体中熔体扩散系数的测量。
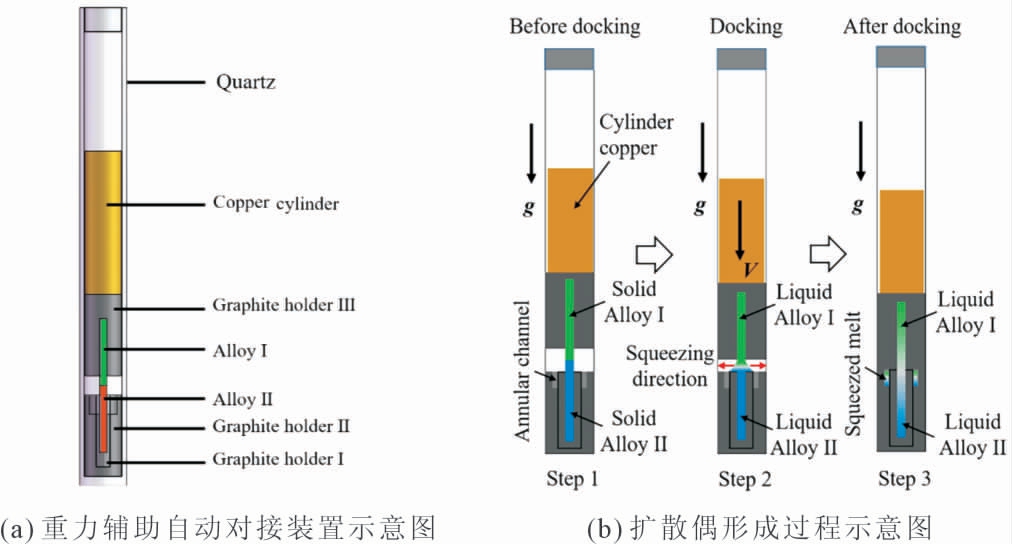
图6 重力辅助自动对接装置、扩散偶形成过程示意图[34]
Fig.6 Schematic diagram of gravity-assisted automatic docking device and the formation process of diffusion couple[34]
2 金属熔体扩散系数测量环境
2.1 常规重力下金属熔体扩散
由于地面环境下金属熔体中不可避免地存在熔体对流,学者们对液态金属的扩散系数的测量方法做了很多尝试和探索以尽量减小测量误差。在前期研究中,主要针对于低熔点金属中的扩散行为,例如Pb、Bi、Sn、Hg、Ga 等。1956 年Yang 等[36]利用长毛细管技术测量了Fe 在Fe-C 合金熔体中的自扩散系数。随后在关于自扩散系数的实验结果中发现,自扩散系数与扩散温度之间的关系主要为以下3种:①Arrhenius 关 系[21,37-39],即lnD 与T-1 成线性关系;②线性关系[40],即D=AT;③幂律关系[41-42],即D=ATn(n=1.7~2.3)。
目前对于金属熔体中原子的互扩散行为的研究主要集中在Al 基、La 基、Cu 基、Fe 基、Si 基、Zr基、Pd 基和Ce 基等合金体系[43-44]。基于传统长毛细管装置、毛细管-熔池装置以及剪切单元装置等测量技术,国内外学者改进且发明了其他的测量方法。
在蓄水池提供的压力下采用剪切单元装置测量SnBi3-Sn 合金中Bi 的互扩散系数,Suzuki 等[22]发现实验结果几乎不受对流的影响,与微重力和磁场下测得的数据一致。1989 年Khandros 等[45]采用X-射线原位测量装置测量了Bi-Sn 合金中Sn 的互扩散系数,该技术根据浓度曲线异常形状能检测到熔体对流等非扩散因素造成的质量传输。随后在2009年,德国宇航中心空间物理材料研究所的研究人员也建立了一套基于X-射线成像技术测量高温合金熔体扩散系数的装置[1]。Kargl 等[46]利用X-射线成像技术结合长毛细管技术和剪切单元技术研究了二元合金熔体中对流与扩散的关系,结果表明由自由表面和温度梯度引起的熔体对流使互扩散系数增加了两倍,且由温度梯度引起的熔体对流使得互扩散系数增加了50%。为在地面环境下更加精确的测量合金熔体的扩散系数,宛波等[47]利用滑动剪切技术和中子衍射相技术结合的方法,测量了Ce80Cu20(at.%)合金熔体的自扩散和互扩散系数,取得了较好的实验结果。
为了能够有效在地面上减小对流的影响,中国科学院物理所的研究人员[48-49]采用复合三层膜的测量方法测量了Bi-In 合金中Bi 的互扩散系数,该方法选用尺寸在几十纳米到几百纳米左右的薄膜和基体材料,使液态金属氧化问题得到解决,测量精度较高。该技术能够有效抑制浮力对流以及Marangoni 对流。此外,Weber 等[50]结合空气动力学理论创造一个无容器悬浮的实验环境(图7),在实验过程中同时采用了激光加热技术、光学高温计的温度测量技术以及X-射线成像或核磁共振(NMR)原位测量技术研究过冷液体的扩散行为。为了避免升温对扩散过程的影响,张博等[2]则在剪切单元测量装置的基础上设计了滑动剪切技术和多层平动剪切技术,该技术有效避免了升温过程对实验结果的影响,但是依旧存在由重力导致的熔体对流的影响。
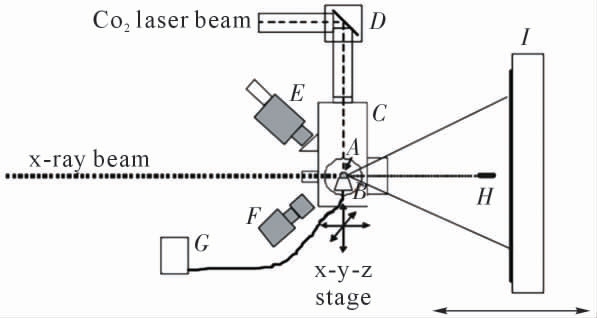
图7 Weber 等实验装置图[50]
Fig.7 Experiment device of Weber et al.[50]
2.2 微重力下金属熔体扩散
合金熔体扩散系数测量最主要的技术难题是熔体对流对测量结果产生影响。而重力环境下不可避免存在熔体对流现象。因此,美国、欧洲、前苏联以及日本的研究者在20 世纪70 年代开始陆续在空间站或运载火箭等微重力环境下开展扩散实验。
1973 年,美国学者Ukanwa 首次在太空中开展金属熔体扩散实验。他采用同位素标记法测量了65Zn 在Zn 中的自扩散系数,并与地面实验数据进行了对比,实验结果表明微重力环境能够一定程度上减小由重力引起的对流,但是由于实验条件的限制,例如温度分布不均匀,测量得到的自扩散系数依旧存在熔体对流的影响。此后,各国研究者们陆续地在微重力实验环境下开展了金属熔体扩散行为的研究。
在空间微重力条件下,Frohberg 等[24]研究了扩散系数与扩散温度之间的关系。研究结果如图8 所示,空间环境下测得的扩散系数(D)与扩散温度的平方(T2)呈线性关系。Masaki 等[31]还首次使用剪切单元装置测量了Co 在Sn 中的热迁移系数。在随后的实验中还发现空间微重力环境有利于研究热迁移行为,这是由于地面环境存在的重力对流会影响热迁移过程。此后,研究者们陆续开展了微重力实验环境下金属熔体扩散系数的研究,其中包括,Pb-Au、Pb-Ag、Pb-Sb[51-52]等合金。1998 年,Itami 等[53]和Kinoshita 等[54]分别使用剪切单元装置研究了液态AgCu 合金和熔融半导体InGaAs 中的扩散行为。
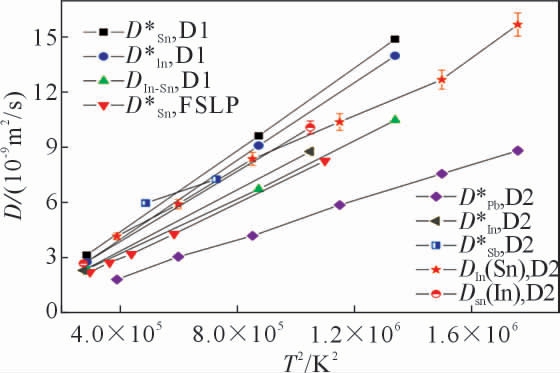
图8 Frohberg 等在微重力环境下测得的D-T2 图[24]
Fig.8 Results of D-T2 plot measured by Frohberg et.al under microgravity environment[24]
综上所述,现有测量技术例如长管技术、剪切单元技术、长毛细管-熔池技术、X-射线成像技术等都存在熔体对流抑制不完全或操作困难等问题,而微重力环境下的实验则因为成本太高且实验技术限制并未广泛开展。目前对于金属熔体扩散的研究还需要进一步深入,对于后续扩散理论的探索还欠缺大量的扩散实验数据,而对于扩散系数的精确测量则需要对测量技术不断的改进来消除熔体对流等不利影响因素。已有研究表明,磁场的施加能显著影响熔体的对流,进而对扩散系数的精确测量产生影响。
2.3 磁场下金属熔体扩散实验进展
由于地面重力的存在,对流所引起的溶质交换将会对扩散系数的测量造成较大影响[23],微重力扩散实验的研究又受到成本以及实验技术的限制并未广泛展开。且Youdelis 等[55]的研究表明,强磁场对原子迁移过程影响很小,因此在液态金属溶质扩散系数的测量实验中施加磁场,利用洛伦兹力抑制熔体对流,为实验结果的精准测量创造一个纯扩散环境是十分可行且具有重要研究意义的。
为了研究金属熔体流速对实验结果的影响,Mathiak 等[41]在In-Sn 合金扩散实验过程中施加不同磁感应强度的强静磁场。随后其[56]采用长毛细管装置(图9)在强静磁场条件下对In-Sn 合金的互扩散系数进行了测量,并将测量得到的互扩散系数与微重力条件下获得的结果进行了对比。结果发现,当垂直磁感应强度高于3 T 时,熔体对流将会被抑制,测量得到的互扩散系数几乎不受熔体对流的影响。但由于采用长毛细管装置,自由表面的存在带来界面张力梯度,从而存在Marangoni 对流,且扩散界面会存在氧化问题,影响后续互扩散系数的测量。此实验中采用双线加热器直接缠绕在试样坩埚外,存在较大的温度梯度,也会造成一定的实验误差。
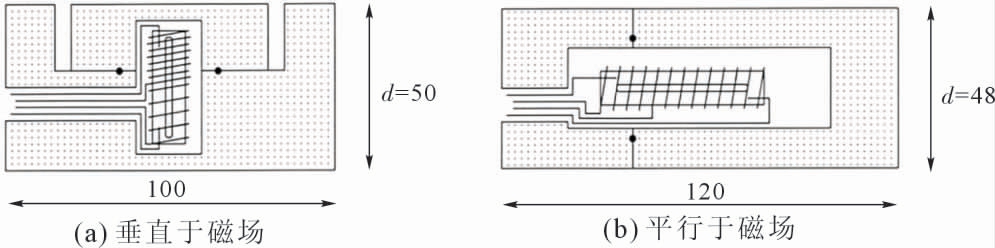
图9 磁场下加热炉中长毛细管放置方向[56]
Fig.9 Direction of long capillary in heating furnace under magnetic Field[56]
利用剪切单元法分别对磁场作用下Sn-SnIn(1 at.%)、Sn-SnBi(0.5 at.%)以及Bi (1 wt.%)在液态Sn 中的互扩散系数测定表明,该数值与微重力条件下测得的互扩散系数吻合较好,证明稳恒磁场能显著抑制对流,可近似看作微重力场[57]。该扩散实验施加磁感应强度为0~0.75 T,磁感应强度不足以完全抑制熔体对流,且剪切单元装置操作过于繁琐,不适用于强静磁场实验环境。
为进一步探究磁场对互扩散系数的影响,Miyake 等[58]在磁感应强度为4 T 的稳恒磁场下采用长毛细管装置测定了In-Sn(In-15 at.%Sn/In-25 at.%Sn)的互扩散系数。结果表明在较高的扩散温度(227~1 000 ℃)下,轴向磁场与水平磁场下测量得到的互扩散系数与Frohberg 等[24]在微重力环境下测量数据吻合,说明了磁场方向的改变对熔体对流的影响没有明显变化,施加4 T 的强静磁场足以完全抑制熔体对流。随后Onishi 等[59]采用相同的实验装置(图10) 研究了水平磁场下In80Sn20、Sn95Pb5 和Ge97.5Si2.5 3种合金的互扩散系数,发现当磁感应强度小于1 T时,In80Sn20 和Sn95Pb5 合金熔体的互扩散系数与微重力环境下的熔体互扩散系数和硬球模型计算的熔点附近的熔体互扩散系数基本一致。但在高温范围内,实验测得的互扩散系数大于模型计算的值。

图10 磁场下互扩散系数测量实验装置示意图[59]
Fig.10 Schematic diagram of experimental device for measuring interdiffusion coefficient under magnetic field[59]
由此可见,液态金属扩散实验中施加稳恒强磁场能显著抑制熔体对流,提高金属熔体扩散系数的测量精度。此外利用强静磁场抑制对流来测量金属熔体扩散系数还具有操作简单、成本低等优点。然而,从现有强静磁场下液态金属的扩散研究结果看来,还存在实验装置缺陷,实验方案不完善造成熔体对流抑制不完全等问题,且缺少更高磁感应强度的磁场对液液扩散行为影响的研究。
上海大学郑天祥等[34-35]在前人研究的基础上设计了新的适用于强静磁场下熔体扩散系数测量的重力辅助自动对接装置,并测量了轴向(0~22 T)和横向(0~2 T)强静磁场下Al-Cu 合金熔体扩散系数。本研究采用Al-Cu 合金的成分分别为Al85Cu15(at.%,熔点约为565 ℃)和Al75Cu25(at.%,熔点约为580 ℃),两者组成Al85Cu15-Al75Cu25(at.%) 扩散偶(平均成分Al80Cu20)。详细实验过程见文献[33]组装好的重力辅助自动对接装置放入电阻加热炉的恒温区,加热炉的恒温区处于轴向/横向磁场的匀强磁场区,见图11(a~b)。扩散温度为700 ℃和750 ℃并保温不同时间(480/600/720/840/960 s)。当等温扩散时间结束后,将试样进行淬火。采用EDS 测量扩散偶轴向上Cu 元素的浓度分布,并利用工业CT 的X 射线获得了扩散偶的二维浓度梯度。
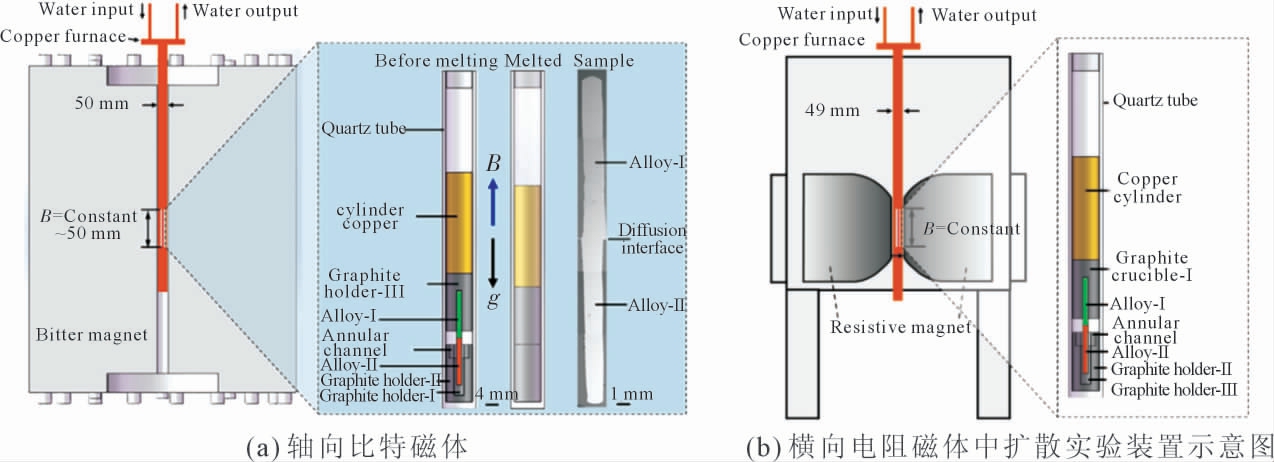
图11 轴向比特磁体和横向电阻磁体中扩散实验装置示意图[34-35]
Fig.11 Schematic diagram of diffusion experimental device in vertical and transverse magnetic field[34-35]
图12(a~b)显示了在700/750 ℃,有/无22 T 超强静磁场下不同扩散时间的浓度分布。扩散从扩散初始界面(位置x0)开始,扩展到没有浓度梯度的位置。图中的实线为修正后的菲克第二定律拟合方程,从图中可以看出,相同扩散时间下,施加22 T 超强静磁场后明显缩短了扩散距离,增大了浓度梯度。
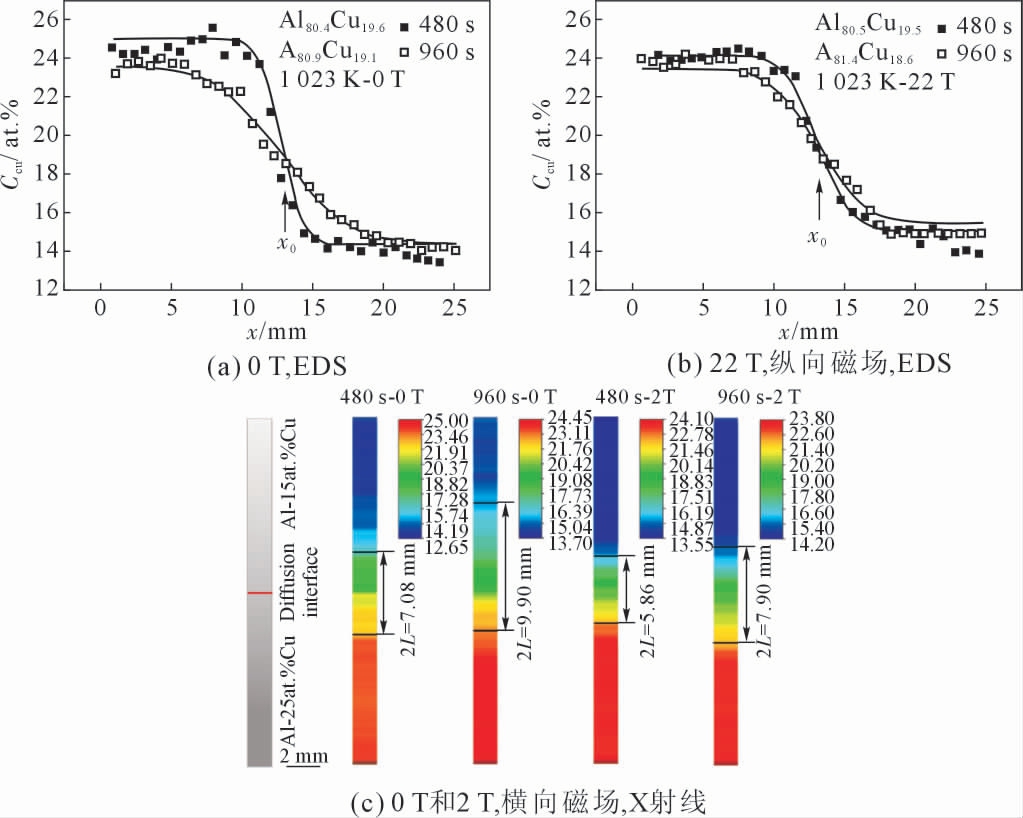
图12 Al-Cu 合金扩散偶在有/无强静磁场下等温扩散后利用EDS 和X 射线测量方法获得的浓度分布图[34-35]
Fig.12 The concentration distribution of Al-Cu alloy diffusion couples after isothermal diffusion under various magnetic fields[34-35]
图13 对比了本实验测量数据与前人研究结果。文献[60-61]报道的扩散数据以及地面实验测得的互扩散系数,由于受到熔体对流的干扰,略高于在微重力条件[62]下测量得到的数据。此外,由于强静磁场对熔体对流的抑制作用,发现在22 T 磁场下测量的Al-Cu 合金熔体互扩散系数值能够与微重力条件下利用X 射线原位观察技术以及剪切单元技术获得的互扩散系数值相媲美,甚至更优。
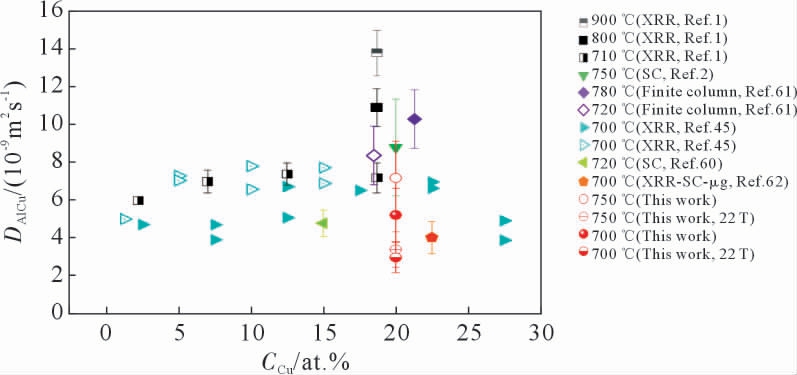
图13 不同Cu 含量下测量的互扩散系数测量结果对比[34]
Fig.13 Comparison of interdiffusion coefficients with previous studies[34]
3 结论及展望
液态金属的扩散是材料、冶金化学领域(如凝固、腐蚀和相变等研究)以及液体物理学中最基本的物理现象之一。因此,准确测量液态金属的扩散系数有助于人们了解金属熔体的原子结构和原子迁移的物理本质,为液态金属原子的扩散机制和物理模型的建立以及后续的材料设计等诸多研究提供实验依据。
作为工业应用合金材料必需的关键参数,更加准确测量合金熔体的扩散系数一直是研究者们所追求的目标,然而目前液态金属扩散系数的测量技术仍然存在很多问题。现有地面环境测量技术都存在熔体对流抑制不完全或操作困难等问题,而微重力环境下的实验则因为成本太高且实验技术限制并未广泛开展。目前中国空间站的逐渐完善,我国科学家有望实现在太空中对合金熔体扩散系数的准确测量。强静磁场已被证实能够抑制导电熔体中的对流,有望在地面上为合金熔体的扩散提供无对流的测量环境。因此,强静磁场也是在地面上创造模拟微重力环境的潜在重要方法。但由于所用实验装置存在诸多问题以及磁场强度不够,熔体中的对流依然存在。本课题组针对上述问题,设计了重力辅助自动对接装置并在高达22 T 强静磁场下开展了扩散系数的测量实验,实验结果已经表明,强静磁场下获得的数据同微重力下相当。同时,随着X 射线,中子衍射等技术的发展,采用该技术测量合金熔体的扩散系数将会进一步提高扩散系数测量的准确性。
目前合金熔体扩散系数的测量已经取得了一些进展,但关于合金熔体扩散系数变化对晶体生长影响的研究十分有限,准确测量熔体中扩散系数并探究扩散系数对晶体生长的影响,以期设计具有优异性能的合金材料是今后值得深入开展的研究方向。
[1]ZHANG B,GRIESCHE A,MEYER A.Diffusion in Al-Cu melts studied by time-resolved X-ray radiography[J].Physical Review Letters,2010,104(3):035902.
[2]GENG Y L,ZHU C A,ZHANG B.A sliding cell technique for diffusion measurements in liquid metals[J].AIP Advances,2014,4(3):037102.
[3]DAS S K,HORBACH J,KOZA M,et al.Influence of chemical short-range order on atomic diffusion in Al-Ni melts[J].Applied Physics Letters,2004,86(1):011918.
[4]GRIESCHE A,ZHANG B,HORBACH J,et al.Atomic diffusion and its relation to thermodynamic forces in Al-Ni melts[J].Defect and Diffusion Forum,2009,289-292:705-710.
[5]高建新,唐国章,齐艳飞,等.金属扩散系数的测量方法与理论研究[J].硬质合金,2012,29(1):46-52.
[6]ROS,U-PFLUMM R,WENDL W,MU¨LLER-VOGT G,et al.Diffusion measurements using the shear cell technique:Investigation of the role of marangoni convection by pre-flight experiments on the ground and during the Foton M2 mission[J].International Journal of Heat and Mass Transfer,2009,52(25-26):6042-6049.
[7]KOMIYA A,MARUYAMA S.Precise and short-time measurement method of mass diffusion coefficients[J].Experimental Thermal and Fluid Science,2006,30(6):535-543.
[8]HORBACH J,DAS S K,GRIESCHE A,et al.Self-diffusion and interdiffusion in Al80Ni20 melts: Simulation and experiment[J].Physical Review B,2007,75(17):174304.
[9]MEYER.A,KARGL F.Diffusion of mass in liquid metals and alloys-recent experimental developments and new perspectives[J].International Journal of Microgravity Science and Application,2013,30:30-35.
[10]MEYER A,STU¨BER S,HOLLAND-MORITZ D,et al.Determination of self-diffusion coefficients by quasielastic neutron scattering measurements of levitated Ni droplets[J].Physical Review B,2008,77(9):092201.
[11]FAUPEL F,FRANK W,MACHT M P,et al.Diffusion in metallic glasses andsupercooled melts[J].Reviews of Modern Physics,2003,75(1):237-280.
[12]GRIESCHE A,KRAATZ K H,FROHBERG G.A modified shear cell for mass transport measurements in melts[J].Review of Scientific Instruments,1998,69(1):315-316.
[13]GRIESCHE A,MACHT M P,GARANDET J P,et al.Diffusion and viscosity in molten Pd40Ni40P20 and Pd40Cu30Ni10P20 alloys[J].Journal of Non-Crystalline Solids,2004,336(3):173-178.
[14]GARANDET J P,BARAT C,DUFFAR T.The effect of natural convection in mass transport measurements in dilute liquid alloys[J].International Journal of Heat and Mass Transfer,1995,38(12):2169-2174.
[15]WAN X,HAN Q,HUNT J D.A diffusion solution for the melting/dissolution of a solid at constant temperature and its use for measuring the diffusion coefficient in liquids[J].Metallurgical and Materials Transactions A,1998,29A:751-755.
[16]HAN Q,HELLAWELL A.Primary particle melting rates and equiaxed grain nucleation[J].Metallurgical and Materials Transactions B,1997,28:169-173.
[17]OIKAWA K,QIN G W,IKESHOJI T,et al.Direct evidence of magnetically induced phase separation in the fcc phase and thermodynamic calculations of phase equilibria of the Co-Cr system[J].Acta Materialia,2002,50(9):2223-2232.
[18]KLASSEN M,CAHOON J R.Interdiffusion of Sn and Pb in liquid Pb-Sn alloys[J].Metallurgical and Materials Transactions A,2000,31A:1343-1352.
[19]KAWAKAMI M,KITAMURA H,YOKOYAMA S,et al.Effect of aluminum and oxygen content on diffusivity of aluminum in molten iron[J].ISIJ International,1997,37(5):425-431.
[20]TANIGAKI M,TOYOTA Y,HARADA M,et al.Mutual diffusion coefficient in molten lead-bismuth mixtures[J].Journal of Chemical Engineering of Japan,1983,16(2):92-98.
[21]CAHOON J,JIAO Y,TANDON K,et al.Interdiffusion of liquid tin[J].Journal of Phase Equilibria and Diffusion,2006,27(4):325-332.
[22]SUZUKI S,KRAATZ K H,FROHBERG G,et al.Impurity diffusion measurements of Bi in liquid Sn using stable density layering and the shear cell technique[J].Journal of Non-Crystalline Solids,2007,353(32-40):3300-3304.
[23]MACLEAN D J,ALBOUSSIÈRE T.Measurement of solute diffusivities.Part I.Analysis of coupled solute buoyancy-driven convection and mass transport[J].International Journal of Heat and Mass Transfer,2001,44(9):1639-1648.
[24]钟浪祥,胡金亮,张博.空间环境下金属熔体扩散研究进展[J].中国材料进展,2017,36(7):492-502.
[25]MATHIAK G,FROHBERG G.Interdiffusion and convection in high magnetic fields[J].Crystal Research and Technology,1999,34(2):181-188.
[26]BOTTON V,LEHMANN P,BOLCATO R,et al.Measurement of solute diffusivities.Part Ⅱ.Experimental measurements in a convection-controlled shear cell.Interest of a uniform magnetic field[J].International Journal of Heat and Mass Transfer,2001,44(17):3345-3357.
[27]GRIESCHE A,MACHT M P,FROHBERG G.Chemical diffusion in bulk glass-forming Pd40Cu30Ni10P20 melts[J].Scripta.Materialia:2005,53(12):1395-1400.
[28]HEUSKIN D,KARGL F,GRIESCHE A,et al.MSL compatible isothermal furnace insert for hightemperature shear-cell diffusion experiments[C]//Journal of Physics:Conference Series Bristol.IOP Publishing,2011.012053.
[29]UJIHARA T,FUJIWARA K,SAZAKI G,et al.New method for measurement of interdiffusion coefficient in high temperature solutions based on Fick’s first law[J].Journal of Crystal Growth,2002,241(3):387-394.
[30]LIU Y,LONG Z Y,WANG H B,et al.A predictive equation for solute diffusivity in liquid metals[J].Scripta Materialia,2006,55(4):367-370.
[31]MASAKI T,FUKAZAWA T,MATSUMOTO S,et al.Measurements of diffusion coefficients of metallic melt under microgravity-current status of the development of shear cell technique towards JEMon ISS[J].Measurement Science and Technology,2005,16:327-335.
[32]耿永亮,朱纯傲,胡金亮,等.一种新的滑动剪切技术测量Al-Cu合金的互扩散系数[J].中国科学:物理学 力学天文学,2014,44(7):728-736.
[33]GRIESCHE A,ZHANG B,SOLÓRZANO E,et al.Note:X-ray radiography for measuring chemical diffusion in metallic melts[J].Review of Scientific Instruments,2010,81(5):056104.
[34]LIU Y,LIN W H,ZHOU B F,et al.A novel gravity-assisted automatic docking device for studying diffusion in liquid metal melts assisted by a strong static magnetic field[J].Review of Scientific Instruments.2021,92(9):094903.
[35]LIU Y,LIN W H,ZHOU B F,et al.Ex-situ study of diffusion in liquid Al-Cu melts under a transverse magnetic field using X-ray imaging[J].Philosophical Magazine Letters,2022,102(4):151-159.
[36]YANG L,SIMNAD M T,DERGE G.Self-diffusion of iron in molten Fe-C alloys[J].JOM,1956,208:1577-1580.
[37]MEYER A.Atomic transport in dense multicomponent metallic liquids[J].Physical Review B,2002,66(13):134205.
[38]DEMMEL F,SZUBRIN D,Pilgrim W C,et al.Diffusion in liquid aluminium probed by quasielastic neutron scattering[J].Physical Review B,2011,84:014307.
[39]DAHLBORG U,BESSER M,CALVO-DAHLBORG M,et al.Diffusion of Cu in AlCu alloys of different composition by quasielastic neutron scattering[J].Journal of Non-Crystalline Solids,2007,353(32-40):3295-3299.
[40]BRUSON A,GERL M.Diffusion coefficients of 113Sn,124Sb,110mAg,and 195Au in liquid Sn [J].Physical Review B,1980,21(12):5447-5454.
[41]MATHIAK G,GRIESCHE A,KRAATZ K H,et al.Diffusion in liquid metals[J].Journal of Non-Crystalline Solids,1996,205-207:412-416.
[42]GRIESCHE A,MACHT M P,SUZUKI S,et al.Self-diffusion of Pd,Cu and Ni in Pd-based equilibrium melts[J].Scripta Materialia,2007,57(6):477-480.
[43]CHAUHAN A S,RAVI R,CHHABRA R P.Self-diffusion in liquid metals[J].Chemical Physics,2000,252(1-2):227-236.
[44]DAVIS K G,FRYZUK P.Application of the fluctuation theory of liquid diffusion to self-diffusion in liquid tin[J].Journal of Applied Physics,1968,39(10):4848-4849.
[45]KHANDROS I Y,OHRING M.A new experimental technique for studying mass transport in liquid metals[J].Journal of Materials Science,1989,24:252-258.
[46]KARGL F,SONDERMANN E,WEIS H,et al.Impact of convective flow on long-capillary chemical diffusion studies of liquid binary alloys[J].High Temperatures-High Pressures,2013,42:3-22.
[47]宛波,胡金亮,钟浪祥,等.Ce80Cu20 合金熔体中原子自扩散与互扩散[J].中国科学:物理学力学 天文学,2015,45(5):76-81.
[48]ZHAO D Q,WANG W H,ZHUANG Y X,et al.Measurement of diffusivity in molten films by a masking film method[J].Physica Status Solidi A-Applications and Materials Science,1999,174(2):337-342.
[49]赵建华,刘日平,周镇华,等.一种测量液态金属扩散系数的新方法—固/液-液/固复合三层膜法[J].物理学报,1999,48(3): 416-420.
[50]WEBER J K R,BENMORE C J,JENNINGS G,et al.Instrumentation for fast in-situ X-ray structure measurements on non-equilibrium liquids[J].Nuclear Instruments and Methods in Physics Research Section A: Accelerators,Spectrometers,Detectors and Associated Equipment,2010,624(3):728-730.
[51]SMITH R W,ZHU X,TUNNICLIFFE M C,et al.The measurement of precise solute diffusion coefficients in dilute liquid metals in a low orbiting laboratory-the influence of g-jitter[C]//Proceedings,first International Symposium on Microgravity Research &Applications in Physical Sciences and Biotechnology.Noordwijk:ESA Publications Division,2000.887-893.
[52]SMITH R W.The influence of g-jitter on liquid diffusion-the QUELD/MIM/MIR programme[J].Microgravity Science and Technology,1998,11(2):78-83.
[53]ITAMI T,KANEKO M,FUKAZAWA T,et al.The study of diffusion in complex metallic liquids with high melting points -the study of self-diffusion and mutual-diffusion of liquid Cu-Ag alloys[J].Journal of Japan Society of Microgravity Application,2000,17:64-69.
[54]KINOSHITA K,KATO H,MATSUMOTO S,et al.InAs-GaAs interdiffusion measurements[J].JASMA,2000,17:57-63.
[55]YOUDELIS W V,CAHOON J R.Diffusion in a magnetic field[J].Canadian Journal of Physics,1970,48(6):905-908.
[56]MATHIAK G,FROHBERG G.Interdiffusion and convection in high magnetic fields[J].Crystal Research and Technology,1999,34(2):181-188.
[57]BOTTON V,LEHMANN P,BOLCATO R,et al.Measurement of solute diffusivities.Part III.From solutal convection dominated transport to quasi-diffusive transport[J].International Journal of Heat and Mass Transfer,2004,47(10-11):2457-2467.
[58]MIYAKE T,INATOMI Y,KURIBAYASHI K.Measurement of diffusion coefficient in liquid metal under static magnetic field[J].Japanese Journal of Applied Physics,2002,41:L811-L813.
[59]ONISHI F,MIYAKE T,INATOMI Y,et al.Measurements of interdiffusion coefficients in metallic melts at high temperature under horizontal static magnetic field[J].Microgravity-Science and Technology,2006,18:86-90.
[60]ZHONG L X,HU J L,GENG Y L,et al.A multi-slice sliding cell technique for diffusion measurements in liquid metals[J].Review of Scientific Instruments,2017,88(9):093905.
[61]LEE N,CAHOON J.Interdiffusion of copper and iron in liquid aluminum[J].Journal of Phase Equilibria and Diffusion,2011,32:226-234.
[62]SONDERMANN E,JAKSE N,BINDER K,et al.Concentration dependence of interdiffusion in aluminum-rich Al-Cu melts[J].Physical Review B,2019,99:024204.