球墨铸铁是一种高强度铸铁,广泛应用于许多对强度、耐磨性等性能要求较高的场合[1],例如各种车床、铣床的主轴等。QT700 是其中具有代表性的材料之一。
金属构件的生产过程中,由于铸造和热处理引起内部的相变或切削、弯曲等冷加工工艺造成零件不均匀塑性变形,都会在零件内部产生残余应力;另外在零件使用过程中,由于与其他零件接触所造成的挤压、磨损等,也会造成残余应力。这些在零件内的残余应力会在实际使用中留下诸多隐患,当零件内部某处残余应力与外部施加应力之和大于材料的屈服强度σs 时,会造成零件在该点的屈服,发生塑性变形,从而使零件失效;当零件内部某处残余应力与外部施加应力之和大于材料抗拉强度时,甚至会造成零件直接在该点断裂[2]。
早在20 世纪30 年代开始,对于金属构件残余应力的测试研究工作就已经展开,但前期的方法对工件的破坏性较大,测量之后的工件无法正常使用。目前,已经出现了多种破坏性残余应力测试方法,如截条法、盲孔法等[3],其中盲孔法操作简单、测量结果精准,且对测试工件破坏很小,打孔后的大型设备大多数情况下仍可以继续使用,因此盲孔法测量残余应力在工程实际中得到了广泛应用[4-6]。在盲孔法测试的过程中,首先要对材料的应变释放系数进行标定。研究者对于灰铸铁[7-8]和系列钢[9-10]的应变释放系数进行了广泛的测试和研究,但目前国内外对于球墨铸铁的应变释放系数的研究相对缺乏。
普通低速钻在钻孔时,会在钻孔过程中产生较大的切削应力[11-12],加上孔边应力集中,容易发生塑性变形,给实验结果带来较大误差,并且操作较为繁琐。现有标准[13]中,给出了高速风钻钻孔的方案,还有研究者采用喷砂工艺钻孔[14],这些做法都是为了降低慢速钻孔带来的不利影响,但是同时也给操作带来了诸多不便。
因此,本文采用便携式高速钻机,研究了QT700 对应于不同应力条件下的应变释放系数。同时鉴于QT700 塑性变形的影响,对测试的应变释放系数进行了塑性修正。
1 盲孔法测量残余应力基本原理
1.1 盲孔法残余应力测试的基本原理
若零件内部存在残余应力σ,在零件上的某一点处钻一盲孔(孔径d,孔深h),盲孔周围的残余应力得到释放,并产生释放应变ε。通常使用应变花测量释放应变ε,再代入公式(1)[15]计算出该点残余应力的大小。图1 为测量残余应力的应变花。
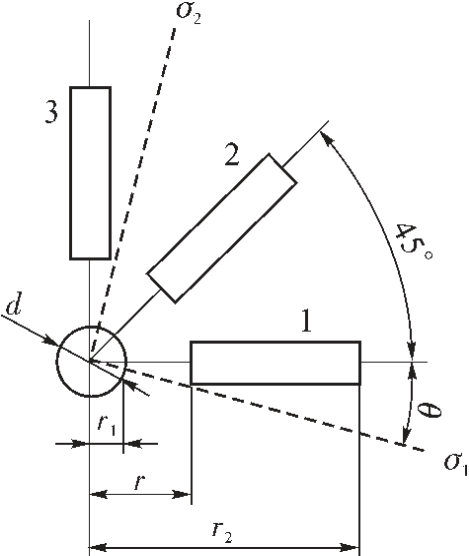
图1 应变花示意图
Fig.1 Schematic of strain rosette
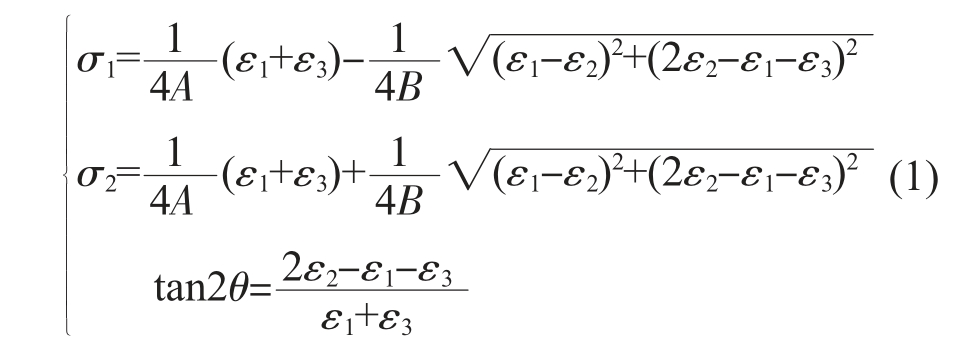
式中,σ1、σ2 分别为最大、最小主应力;ε1、ε2、ε3 分别为1 号、2 号、3 号应变片测得的释放应变;θ 为σ1与1 号应变片之间的夹角;A、B 为材料的应力释放系数;E 为材料的弹性模量。
1.2 应变释放系数标定的原理
应变释放系数A、B 值与盲孔尺寸以及材料的力学性能有关,在通孔情况下,应变释放系数A、B值可由Kirsch 理论[16]直接求得:
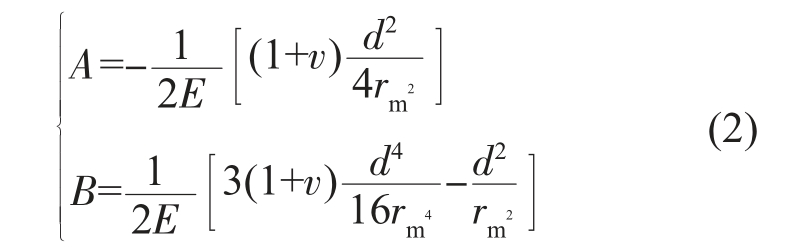
式中,E、v 分别为材料的弹性模量和泊松比;d 为钻孔的直径;rm 为应变花的平均半径。
盲孔法的应变释放系数则需要进行实验标定,应变片1、3 分别平行于σ1、σ2 方向,此时θ=0,代入公式(1)可得到如下公式:
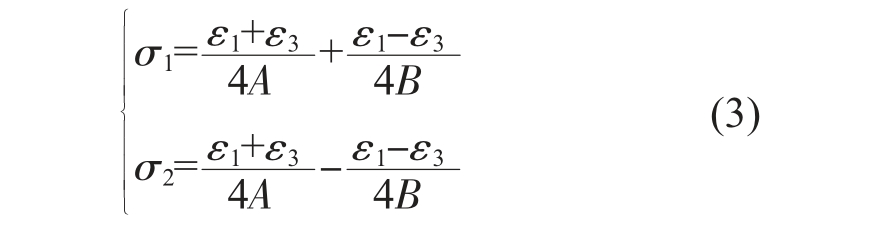
在应变释放系数标定试样上施加单向应力场(σ1=σ,σ2=0),代入式(3),可得到关于应变释放系数A、B 值公式:
根据1、3 应变片采集的应变ε1、ε3 即可求得应变释放系数A、B 值。
2 应变释放系数标定实验
2.1 QT700 应变释放系数标定试样制备
(1)QT700 试块制备 在模具中浇铸尺寸为50 mm×50 mm×300 mm 的试块,将试块进行去应力退火处理,退火温度为650 ℃,退火时间4 h。
(2)精加工 按图2 所示尺寸进行线切割和精磨,试样拉伸性能如表1 所示。
表1 QT700应变释放系数标定试样拉伸性能
Tab.1 Tensile properties of QT700 strain release coefficient calibration sample

(3)试样表面制备 将待测量的表面首先用砂纸打磨,除去锈迹及氧化层,并且使表面粗糙,便于之后应变花的粘贴。用划针在表面划出待粘贴应变花的位置,用酒精将试样表面清洗干净,去除残留的金属粉末。
(4)粘贴应变花 在划针标记位置滴一滴502胶,将应变花平整地粘贴在试样表面,尽量保证1 号应变片与拉伸方向一致,按照国家标准GB/T31310-2014,在标定试样中心粘贴一个应变花记录应变,在其两侧粘贴监视电阻应变花,使其读数差值小于5%。本文选用免焊接应变花,简化了粘贴应变花的操作,应变花外接导线被绝缘胶皮包覆,将导线粘贴在试样表面即可。
2.2 所用实验设备
应变花型号为BFH120-3CA-D150 型三向应变花,电阻值120 Ω,灵敏系数2.0±1%;应变仪及相关测试软件为江苏东华测试技术股份公司的DH5922N 动态信号测试分析系统。
拉伸设备为MTSLandmark 370.25 电液伺服金属疲劳试验机,最大加载载荷250 kN,加载频率0~50 Hz;钻孔设备为高速钻机(90 000 rpm,合肥吉纳新材料科技有限公司)和配套的圆柱形铣刀(刃径2 mm)。
2.3 标定实验
将准备好的QT700 标定试样安装在MTS 试验机上,将应变片的导线与应变仪相连接。根据表1 中QT700 试样的抗拉强度σb 计算加载应力,每拉伸0.05 σb 暂停15 s 左右,在拉伸应变曲线图上留下一段平台,便于记录数据。试验机的加载等级如表2 所示,同时在动态应变仪上采集应变数值。
表2 加载力等级
Tab.2 Loading force level
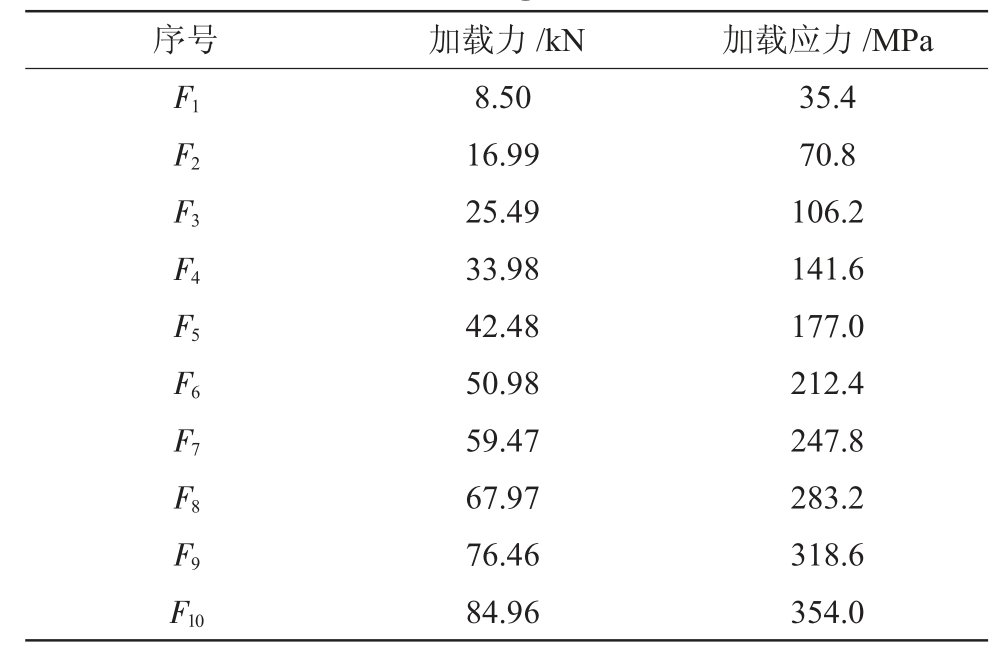
加载完成之后卸载并将试样取下,在试样上钻盲孔(φ2 mm×2.5 mm),本实验使用便携式钻机(最大转速可达90 000 rpm),安装圆柱形铣刀,在钻孔时减小对孔边切削应力,从而减小给实验结果带来的误差。
根据圣维南原理[17],当盲孔的孔深大于等于其孔径时,所测应变释放系数与通孔情况较为接近,另外根据国家标准GB/T 31310-2014,孔深大于1.2 倍孔径即可,大于1.2 倍孔径对结果无明显影响。结合应变花尺寸,本实验钻孔的孔径与孔深分别为φ2 mm 与2.5 mm。
钻孔之后将试样再次在MTS 试验机上按表2加载等级进行拉伸,在应变仪上记录应变数值。将钻孔后得到的各向应变与钻孔前所得应变相减,可得各加载等级下的释放应变值,代入公式(4)即可求得应变释放系数。
3 实验结果及塑性修正
3.1 实验结果
对钻孔前和钻孔后的试样进行加载,得到的3个应变花钻孔前及钻孔后的应变数值如表3 所示,钻孔前后的拉伸应变曲线分别如图3(a~b)所示。
表3 钻孔前后拉伸应变
Tab.3 Tensile strain before and after drilling
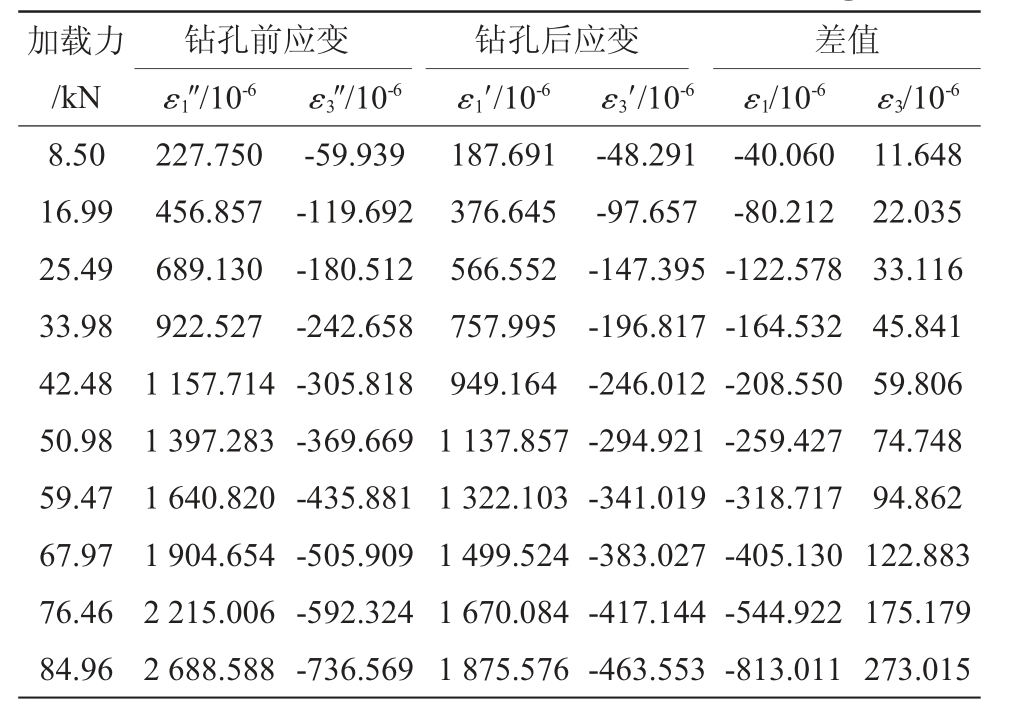
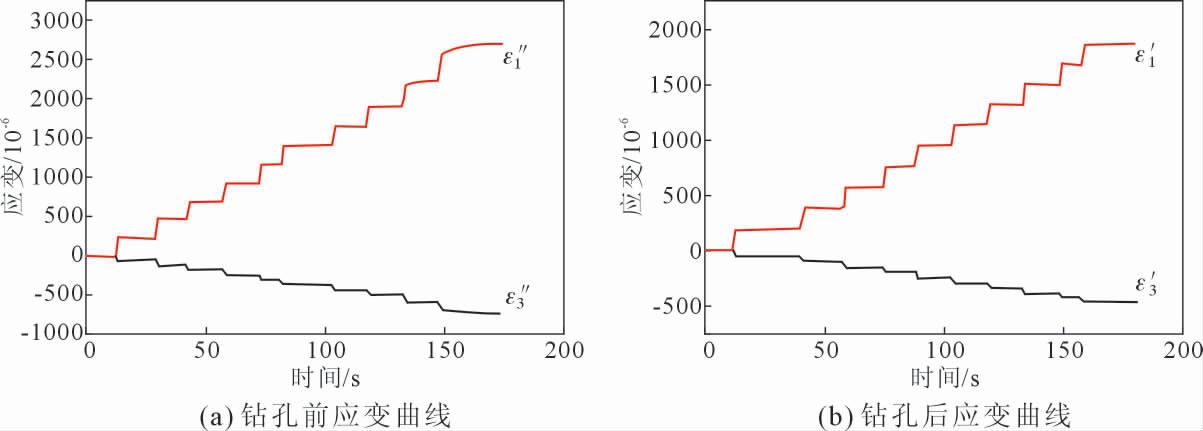
图3 钻孔前后应变曲线
Fig.3 Strain curve before and after drilling
将钻孔后得到的各向应变与钻孔前所得应变相减得到的释放应变值代入公式(4),求得应变释放系数,计算结果如表4 所示。图4 是由应变花记录数据计算出的应变释放系数与加载载荷的关系。
表4 实测的QT700应变释放系数
Tab.4 Measured QT700 strain release coefficient
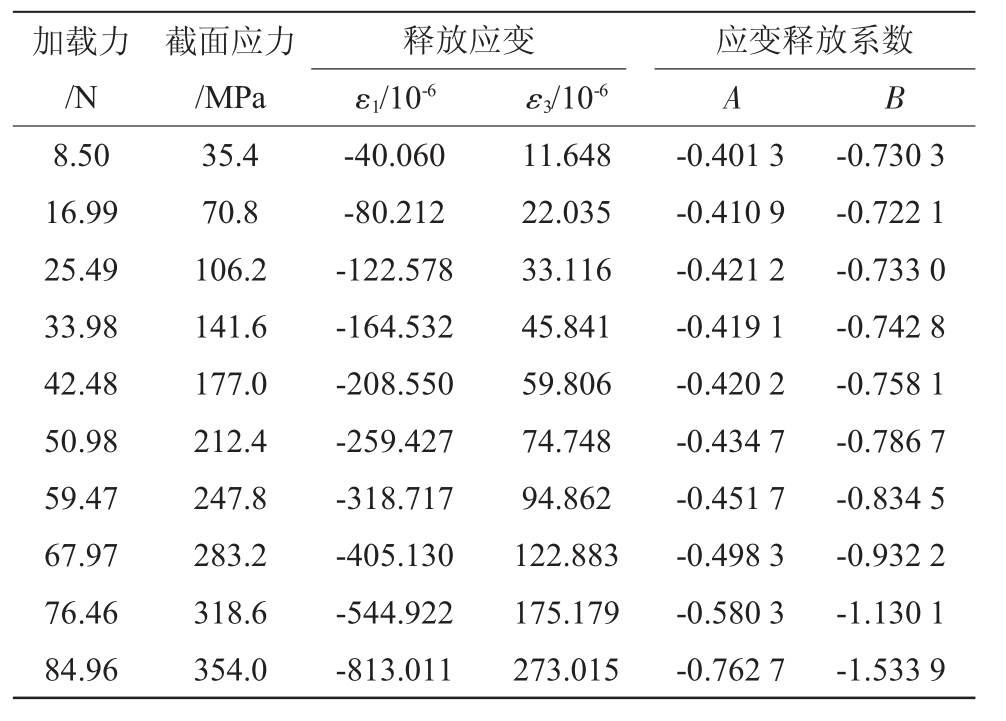
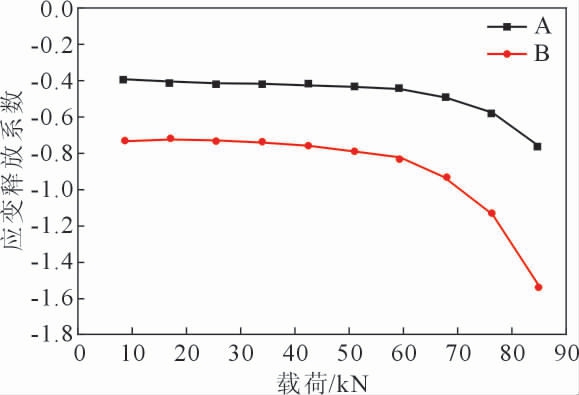
图4 应变释放系数与载荷的关系
Fig.4 Relationship between strain release coefficient and load
当加载载荷引起的截面应力大于σs/3 时,由于孔边应力集中,在拉伸时孔边会发生塑性变形。根据表1 可知本实验所用QT700 材料的屈服强度σs为427 MPa,加载力F1 至F4 引起的截面应力均小于σs/3,而当加载力大于F4 时引起的截面应力均大于σs/3,在该应力状态下得到的应变释放系数需对其进行塑性修正。从图4 也可以看出在小载荷下的应变释放系数基本一致,曲线基本保持水平,当加载载荷逐渐增大,加载载荷引起的截面应力大于σs/3,孔边开始产生塑性变形,应变释放系数曲线开始迅速下降。弹性阶段所标定的应变释放系数A、B 值平均值为:
3.2 塑性修正
3.2.1 孔边塑性变形引起的误差
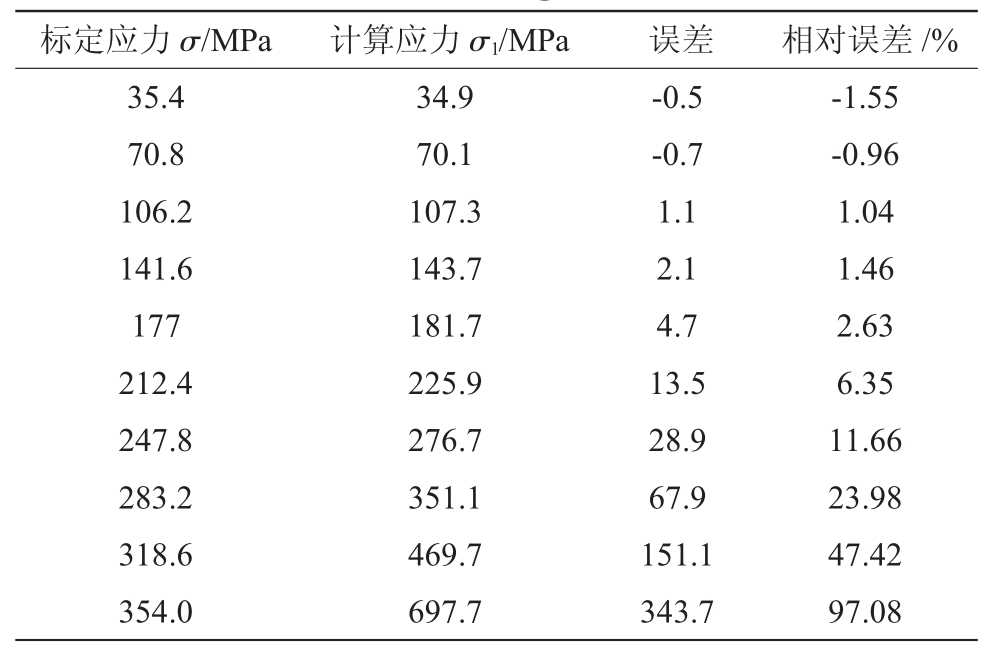
对QT700 试样作大拉力标定实验,将得到的应变释放系数A、B 值代入式(3),计算得到的应力σ1与标定应力σ 相比,误差如表5 所示。从表5 可以看出,在应力水平较低时(σ<σs/3),由应变释放系数A、B 计算得到的应力误差较小,当σ>σs/3 时,由于孔边应力集中引起的塑性变形使得误差明显增大,此时弹性理论不再适用,需要对测量结果进行塑性修正。
表5 孔边塑性变形引起的应力误差
Tab.5 Stress error caused by plastic deformation at hole edge
3.3 塑性修正公式的推导
Mises 屈服准则是指物体中某一点的应力状态达到一数值时,在该点位置就会发生屈服,在研究盲孔法测量残余应力的过程中,只考虑平面应力问题,Mises 屈服条件可表示为:
根据广义胡克定律:
代入式(6)中,则式(6)的左边部分可表示为:
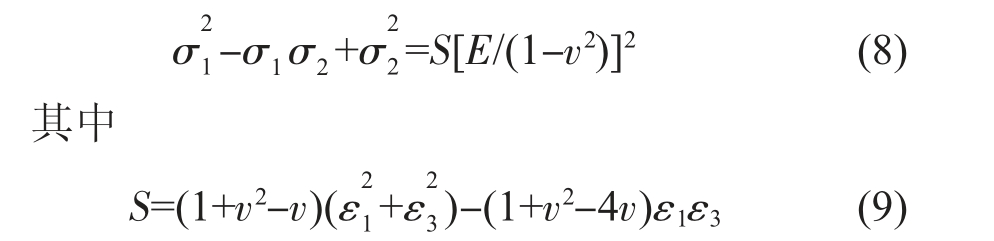
结合材料力学中形状改变比能理论,可知S 反映的是在相应应力(应变)状态下形状改变比能的大小。当S 达到一极限数值时,孔边即开始发生塑性变形。
将实验数据代入式(9),计算出各级应变的参量S。图5 是参量S 与应力σ 间的关系,从图中可以看出应力增大,参量S 也随之增大,二者成近似指数关系。
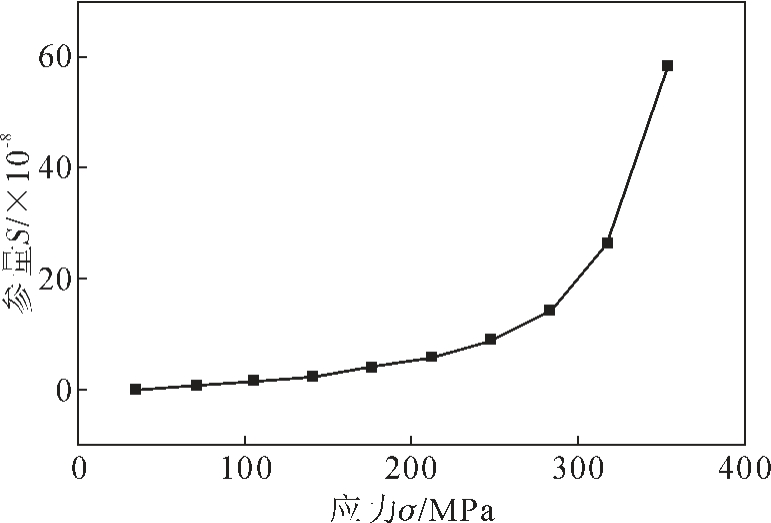
图5 参量S 与应力σ 间的关系
Fig.5 The relation between parameter S and stress σ
图6 是应变释放系数A、B 与参量S 间的关系,从图中可看出参量S 较小时,此时孔边未发生塑性变形,应变释放系数变化不大。当参量S 达到一极限数值时,受孔边塑性变形影响,应变释放系数A、B 值均开始减小,二者近似成线性关系,对其作线性拟合,得到修正后的应变释放系数A、B 值与参量S之间的关系。
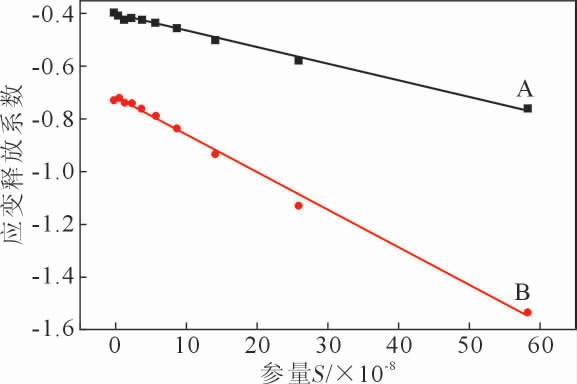
图6 应变释放系数与参量S 间的关系
Fig.6 The relation between strain release coefficient and
parameter S

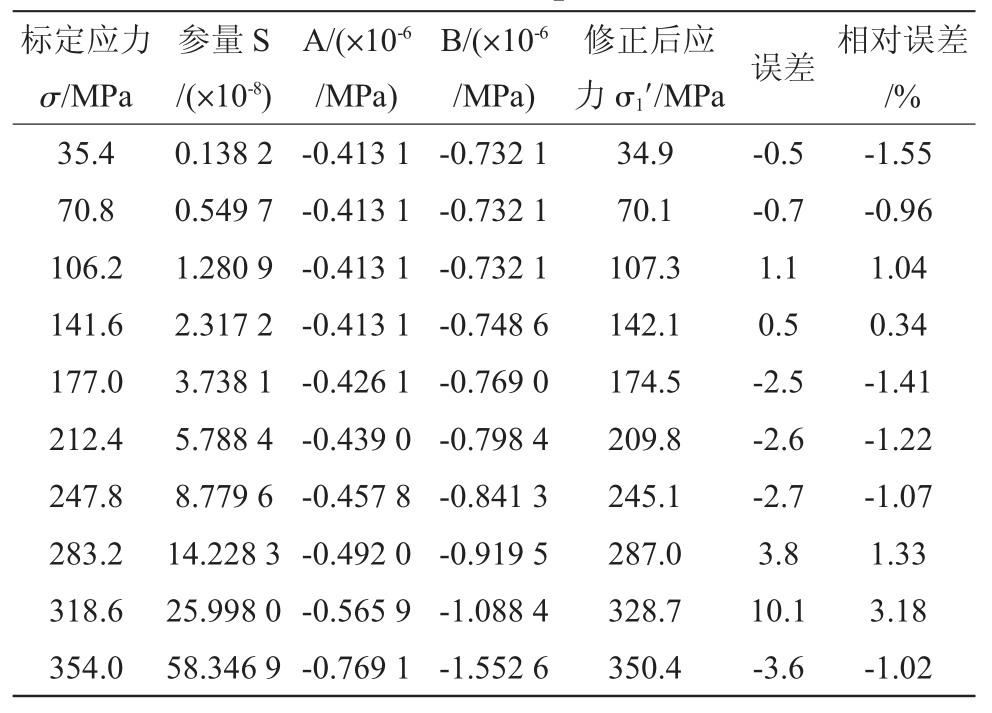
式(10)及(11)为应变释放系数A、B 经塑性修正后的公式。表6 为经塑性修正后的误差,从中可以看出在大应力状态下,经修正后的应变释放系数A、B 计算的到的应力σ1′与标定应力σ 相比,误差降低了很多。与表5 相比,经塑性修正后的最大相对误差由未修正的97.08%减小到3.18%,测量精度大幅提高。
表6 经塑性修正后的应力误差
Tab.6 Stress error after plastic correction
4 结论
(1)采用盲孔法对QT700 铸件进行了应变释放系数进行了标定,改进了盲孔法中最重要的钻孔步骤,在小型钻床上安装转速高达90 000 rpm 的高速钻及圆柱形铣刀,减小了采用低速钻及普通钻头在钻孔时产生的应力,提高了测量精度。
(2)从对QT700 试样的应变释放系数标定结果可以看出,在标定应力相对较小的情况下,各标定应力下应变释放系数A、B 值基本一致,当标定应力σ 达到177 MPa(σ/σs=0.41)时,应变释放系数A、B值开始明显随应力增大而减小。
(3)对标定得到的应变释放系数A、B 值进行塑性修正,由于孔边应力集中会给实验结果带来一定误差,当形状改变比能S 达到一定值时,应变释放系数A、B 值必须进行修正。修正之前的A、B值计算应力与实际标定应力相比,最大相对误差达到97.08%,经塑性修正后的最大相对误差仅为3.18%。
[1]盛达.球墨铸铁工业生产60 年的发展[J].现代铸铁,2009,29(2):56-60.
[2]王娜.中厚板焊接残余应力测试的盲孔法研究[D].大连:大连理工大学,2007.
[3]林丽华,陈立功,顾明元.残余应力测量技术现状及其发展动向[J].机械,1998(5):47-50.
[4]MATHAR J.Determination of initial stresses by measuring the deformations around drilled holes[J].Transactions of the American Society of Mechanical Engineering,1934,56(4):249-254.
[5]SOETE W,VANCROMBRUGGE R.An industrial method for the determination of residual stresses[J].Transactions of the American Society of Mechanical Engineering,1950,8(1):17-28.
[6]SANDIFER J P,BOWIE G E.Residual stress by blind-hole method with center hole [J].Experimental Stress Analysis,1978,1(5):173-179.
[7]潘光东,王文洁,董志鹏.HT250 材料应力释放系数值的确定[J].现代铸铁,2009(1):87-89.
[8]钱海盛,张宇,郭汉徳,等.盲孔法测量HT300 铸件残余应力的应变释放系数研究[J].热加工工艺,2016,45(19):80-83,86.
[9]BEANEY E M.Accurate measurement of residual stress on any steel using the centre hole method[J].Strain,1976,12(3):99-106.
[10]候海量,朱锡,刘润泉.盲孔法测量921A 钢焊接残余应力的应变释放系数研究[J].船舶工程,2003,25(1):57-60.
[11]WANG C C.A study on the induced drilling stress in the center hole method residual stress measurement[J].Strain,1992,28(2):45-51.
[12]MICHAEL T.Brief investigation of induced drilling stresses in the center hole method of residual stress measurement[J].Experimental Mechanic,1982,22(1):26-30.
[13]ASTM Standard E837.Standard test method for determining residual stresses by the hole-drilling strain gage method[S].
[14]王晓洪,赵怀普.盲孔法测量残余应力原理及几种打孔方式介.第15 届全国残余应力学术交流会论文[C].2009.
[15]侯海量,朱锡,刘润泉.盲孔法测量焊接残余应力应变释放系数的有限元分析[J].机械强度,2003,25(6):632-636.
[16]李华.盲孔法测量非均匀残余应力时释放系数的研究[D].合肥:合肥工业大学,2012.
[17]韩敬鉴,雷宏刚,路国运,等.基于盲孔法的焊接空心球节点网架中无缝钢管表面残余应力的测试研究[J].土木工程,2020(5):366-381.