蠕变可定义为固体材料在承受恒定载荷或应力（低于材料屈服强度）时缓慢且连续的变形[1]。 蠕变断裂是指材料在恒定应力下的连续变形，直至断裂失效，是合金中常见的高温机械故障之一[2]。 在高温高压下服役的金属零件不可避免地会产生与时间、应力、以及温度有关的蠕变行为。 当应力到达到材料的蠕变极限时，会发生蠕变断裂失效[3]，同时加上压力、 温度变化引起的应力波动带来的疲劳，会产生高温蠕变疲劳失效问题，进一步降低了在服役工况下产品的寿命，所以，合金产品的使用寿命严重受到材料蠕变性能的限制[4]。
虽然高温合金的蠕变断裂寿命可以通过试验方法确定，但高温蠕变试验通常需要几十小时才能完成，合金制造以及测量成本很高[5]。 而且用于高温应用的先进合金的设计需要考虑多组分、多相、多种物理因素以及不同尺度的多种描述符， 仅仅通过试验来促进这种复杂的研究是十分困难的，所以，研究人员希望能够对合金性能进行预测[6]。
经过数年的努力， 针对合金性能预测的研究成果显著。本文系统总结了蠕变断裂寿命的预测方法，包括传统的基于理论计算的模型、 利用声发射技术以及最近采用信息学工具如机器学习方法对蠕变寿命进行的预测， 并概述了以上方法的优势以及可能存在的问题。
1 蠕变寿命预测的传统方法
前人提出了几种加速预测合金蠕变断裂寿命的理论方法。 大致可以分为几类，包括时间-温度参数(Time-Temperature Parameter,TTP)方法和蠕变本构模型(Creep constitutive model,CCM)[7]以及利用声发射信号进行寿命预测等。
1.1 基于时间温度参数（TTP）方法的寿命预测
时间-温度参数方法最为传统，它的一个显著特点是，通过将蠕变寿命与外加应力和温度关联起来，可以将代表不同实验温度的多条蠕变断裂曲线叠加到主曲线上，这种数据处理方法可以在很大程度上缩短试验时间[8]。 其主要模型如公式(1)所示：
式中，T 是以华氏度为单位的温度；tr 是以小时为单位的断裂时间；P 是tr 和T 的函数；f(σ)是应力的函数，定义主曲线。 一旦确定f(σ)，就可以快速的计算出给定应力和温度下的断裂时间[9]。
作为依赖时间与温度对材料蠕变断裂寿命进行预测的方法中的一种， 参数化数值等温数据(Parametric Numerical Isothermal Datum, P-NID)建模方法可以以更高的精度表示数据， 并且该模型和数据之间的有密切的对应关系。 Bolton[10]发现该方法在外推中满足适当的可靠性标准，并且证明了采用该方法在中低实验温度下，断裂时间可以外推超过15 倍。 该方法通过建立应力和断裂时间之间的经验关系，将常规认为必要的总测试时间减少到不到1/10。 随后，Bolton[11]为了验证P-NID 模型的准确性与可靠性， 又采用4 组大型数据集(2.25Cr1Mo、11%CrMoVNb、304H SS 和Incoloy 800)对该方法进行验证，证明了该方法在有限数据的近30 倍的外推化上的可靠性。
Dang 等[8]使用Larson-Miller(LM)模型和Manson-Haferd（MH）模型，在650~850 ℃的温度内预测Inconel 740 和740H 的长期蠕变断裂寿命。 蠕变断裂值的LM 模型和MH 模型描述如公式(2)、(3)所示：
式中，PLM 与PMH 分别为蠕变断裂值的LM 和MH 描述；C 是LM 中的材料常数；Ta 和logta 是MH 中的材料常数，其值通常由实验数据所得，两者呈线性关系。 LM 方法表示观察到的函数与logtr 恒定应力下温度倒数的近似线性关系，而MH 方法表示与温度的近似线性关系。 用短期数据对两种合金蠕变寿命的预测结果如图1 所示。结果证实在该数据集中，对于MH 参数，由短期数据和整个数据集得到的预测结果与实验数据吻合得很好。
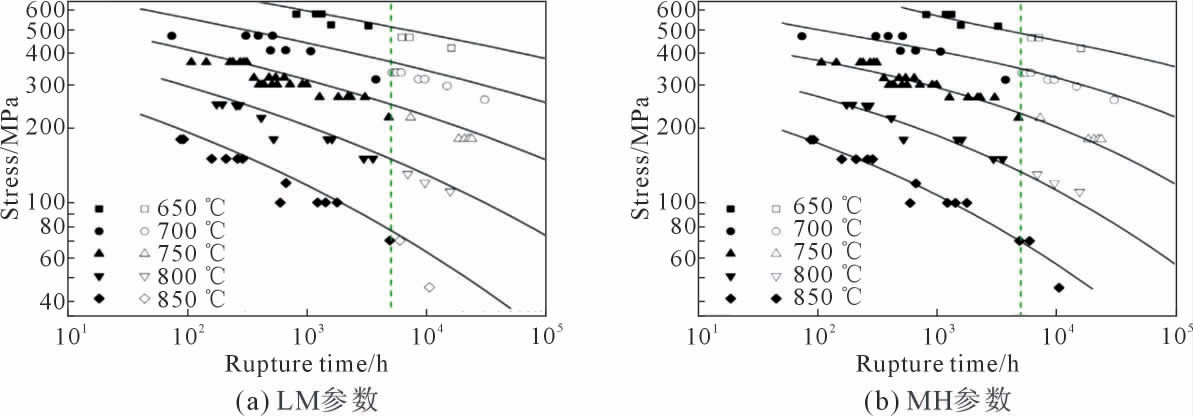
图1 使用时间-温度参数，利用tr≤5 000 h 的短期数据集，比较Inconel 740 和740 H 的蠕变破裂预测曲线和实验数据；虚线是短期和长期实验数据的边界[8]
Fig.1 Comparison of Inconel 740 and 740 H creep fracture prediction curves with experimental data using time-temperature parameters,using a short-term data set tr≤5 000 h;The dotted line is the boundary between short-and long-term experimental data[8]
因为传统方法与蠕变断裂数据不完全匹配，并且对长期蠕变寿命的预测总是存在高估现象， 而多常数法与蠕变断裂数据显示出良好的一致性。 所以Kim 等[12]为了准确预测Inconel 617 合金在900 ℃以上的长期蠕变强度，用具有两个C 值的多常数方法预测了Inconel 617 合金的长期蠕变寿命，而不是采用只有单一常数C 的Larson-Miller(LM)模型的常规方法。 采用双常数LM 模型与传统模型对Inconel 617 合金进行预测的结果对比见图2。 在950 ℃下105 h，常规方法的蠕变强度为7.2 MPa，但对于多常数方法，蠕变强度降低至4.7 MPa。 多常数法与蠕变断裂数据显示出良好的一致性，可准确预测Inconel 617 合金的长期蠕变断裂。
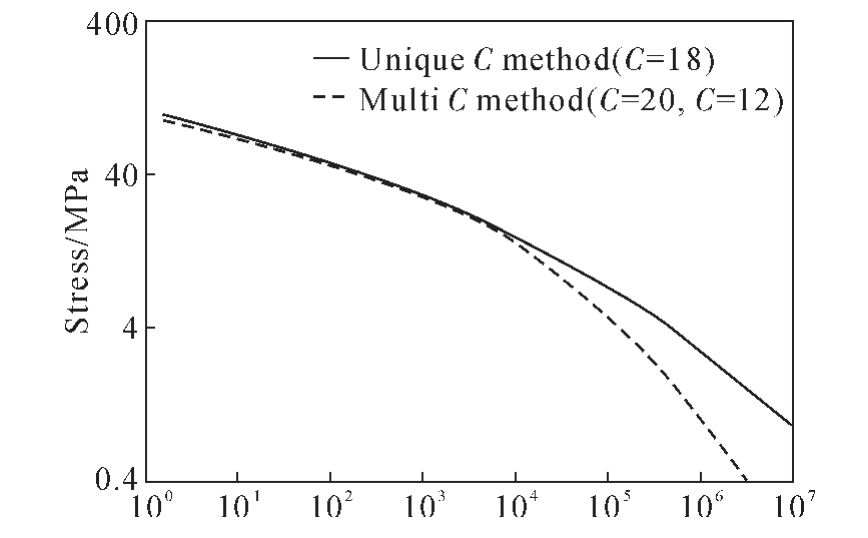
图2 在950 ℃时由单一常数和多常数方法预测的蠕变强度对比曲线[12]
Fig.2 Comparison of the creep strength curves predicted by the unique C and multi C methods at 950 ℃[12]
然而， 这些TTP 方法基于实验数据的实证分析，大多缺乏统一的理论基础。 此外，他们没有充分考虑到实际蠕变过程中的微观结构演变信息[7]。 而且，该方法对数据有较强的依赖性，对于不同来源的实验数据有可能出现不同的结果。
1.2 基于蠕变本构模型（CCM）的寿命预测
随着晶体塑性理论和连续力学的推广， 用于预测蠕变寿命的蠕变本构模型近年来发展迅速。 连续介质损伤力学理论不仅描述材料的损伤行为， 而且讨论宏观裂纹的形成过程， 并从材料科学和连续介质力学的角度研究损伤变量的演化及其对材料寿命的影响[13]。目前，国内外学者采用损伤力学原理对蠕变损伤、蠕变疲劳损伤进行了大量研究，并基于宏观变形行为提出了许多预测材料在蠕变疲劳交互作用下寿命估算模型。
MacLachlan 和Knowles[14]发展了一种改进的损伤力学方法来模拟现代单晶高温合金的应力断裂特性，其采用改进的连续损伤模型(CDM)结合与蠕变变形和微观结构变化相关的描述符， 对4 种单晶高温合金的应力断裂性能进行了模拟和预测。 以RR2000 为例， 其断裂数据与文中所建模型的拟合结果如图3，可见拟合效果良好。
图3 RR2000 应力断裂数据和文中描述模型的拟合[14]
Fig.3 RR2000 stress rupture data and fits obtained using the equations described in the text[14]
随后，Feng 等[15]提出了一种用于解释蠕变损伤的各向异性连续损伤模型， 该模型基于连续损伤力学(Continuous Damage Mechanics, CDM)的各向异性损伤力学模型来模拟单晶高温合金的蠕变行为，不仅可以测量损伤程度，还考虑了损伤的各向异性。所建立的损伤晶体模型能够反映微观组织， 证实晶格取向、自硬化、潜在硬化和速率敏感性等对蠕变和损伤发展有很大影响。
Prasad 等[16]从位错运动和界面位错网络造成的损伤出发，对不同载荷下的蠕变行为进行了建模,建立的模型用于模拟<001> 取向单晶镍基高温合金的单轴蠕变，预测结果如图4。 不难发现理论预测与高温合金CMSX-4 的实验数据吻合良好。
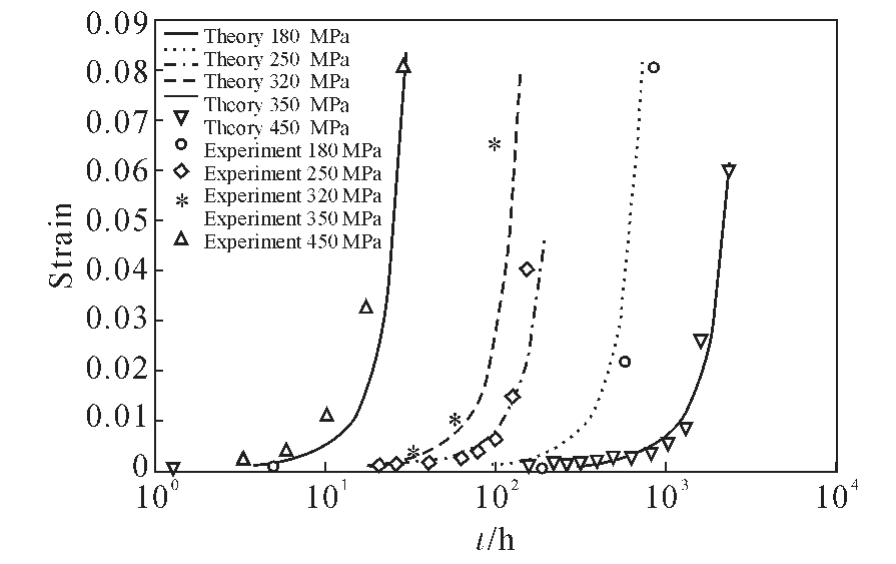
图4 CMSX-4 沿<001>方向加载时应变随时间的变化(h=950 ℃)：模型预测与实验结果的比较[16]
Fig.4 Strain variation with time when CMSX-4 is loaded along<001>direction(h=950 ℃):comparison of model prediction and experimental results[16]
随后，Prasad 等[17]又对该本构理论进行了扩展以描述单晶镍基高温合金中与晶体取向相关的蠕变各向异性。 扩展后的模型用于模拟单晶镍基高温合金CMSX-4 沿<001>、<111> 和<011> 方向加载时的单轴蠕变，得到了令人满意的结果。
Vladimirov 等[18]考虑了单晶合金蠕变各阶段的位错运动特征， 建立了一个扩展的Cailletaud 单晶塑性模型， 该模型是通过为每个滑移系统引入一个标量损伤变量的附加演化方程来实现的。 拟合结果如图5 所示。与单轴和多轴试验数据的比较表明，该扩展材料模型与试验结果吻合良好， 可用于模拟单晶高温合金的一次蠕变、 二次蠕变和三次蠕变以及寿命估算， 目前该模型已经应用于研究镍基单晶高温合金LEK94。
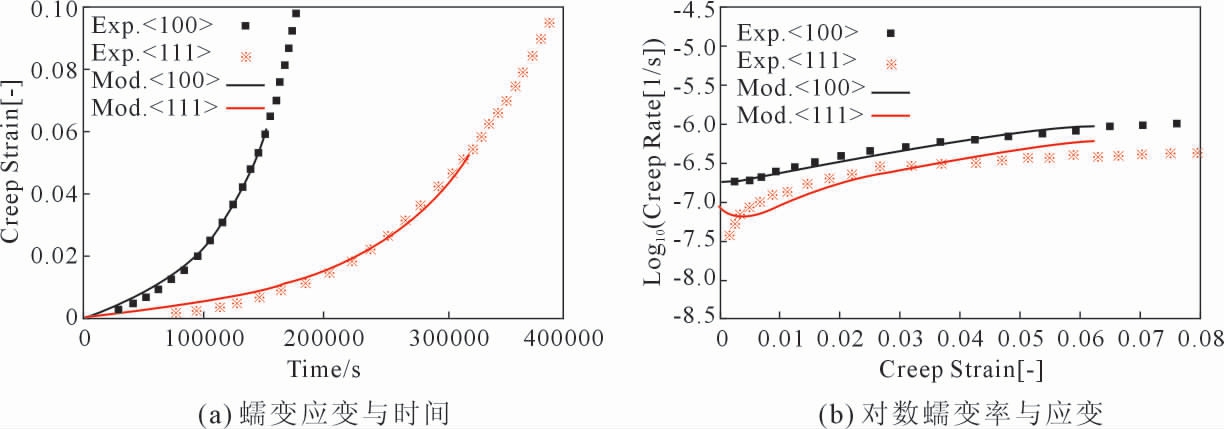
图5 取向<100>和<111>,σ=200 MPa 和T=1 020 ℃的参数拟合[18]
Fig.5 Parameter fitting for crystallographic orientations<100>and<111>,σ=200 MPa and T=1 020 ℃[18]
同样是镍基高温合金，Fedelich 等人[19]建立了单晶高温合金高温力学行为的本构模型并引入了微观结构参数，以考虑γ 相筏化引起的变化及其对合金蠕变的影响。 该模型能够表示筏化后高应力下的机械软化且已应用于模拟几种晶体取向的单轴蠕变过程中的筏化，包括缺口试样和循环加载试样，已被证明能够描述CMSX-4 合金在高温大范围载荷条件下的力学行为和筏化动力学。
为进一步加速蠕变特性的建模，Kim 等人 [20]通过对已有模型的修正和组合， 建立了一个基于微观组织、 工艺和蠕变条件以及材料性能的镍基高温合金中温蠕变性能预测模型并进行了修改， 以便根据CALPHAD(相图计算)热力学计算确定尽可能多的必要模型参数。 模型如公式(4)所示：
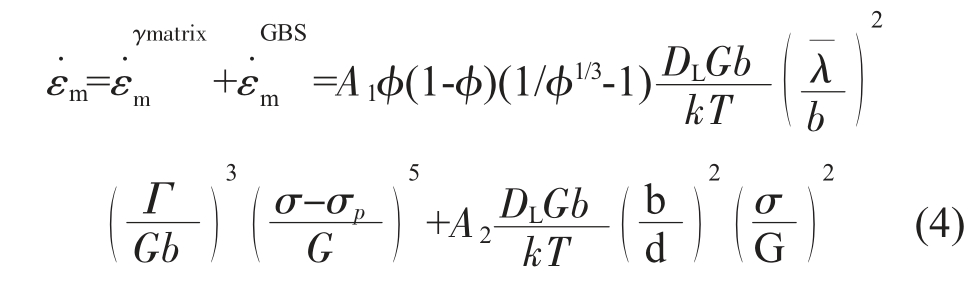
式中，DL 是晶格扩散系数；G 是剪切模量；b 为伯氏矢量；k 为波尔兹曼常数；T 为绝对温度；Γ 为堆叠层错能；σ 为外加用力；σp 为反向应力；φ 为γ′沉淀的体积分数；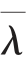
为γ′析出相的粒子间距；d 为晶粒尺寸；A1 和A2 为可调模型参数。 该模型可以重现各种镍基高温合金的最小蠕变速率、 蠕变断裂时间和比应变时间，与实验数据有很好的对应，无需进一步的蠕变实验。但该法仅限中间温度的蠕变性能预测，不适合研究高温蠕变。
相对于匀质体，大多数材料固有异质性，即使在相同的条件下， 也会导致较大的样品间寿命波动[21-23]，因此，对于非匀质材料的蠕变断裂寿命的预测同样受到研究人员的关注。Koivisto 等[24]将纸张作为一种非均质材料来研究其蠕变变形， 通过粘弹性纤维束模型的模拟， 说明了变形局部化如何控制蠕变曲线的形状，从而控制寿命可预测性的程度。文章展示了如何通过利用样品固有蠕变曲线中的“通用”特征， 特别是通过加速蠕变速率来预测单个样品的寿命。目前，纸张样品使用该方法能够粗略地预测样本蠕变断裂曲线的最后20%。
以上采用本构模型对蠕变寿命进行预测虽已取得良好的成果，但采用蠕变本构模型(CCM)对材料的蠕变性能进行预测存在一个问题， 即试验参数很难做到全面， 也很难全面考虑到某些与蠕变高度相关的微观组织结构演化信息，如晶格参数、层错能等。
1.3 利用声发射及散斑成像预测蠕变寿命
以上方法通过公式的建立、 模型的构造来对材料的蠕变断裂寿命进行预测， 而没有考虑断裂过程中所发出的更为直观的物理信号如断裂过程中所发出的声信号。 数千年前人们通过听声识别材料内部的缺陷或损伤。 如今专业人员通过声发射(AE)对材料的损伤及其机理进行识别和研究。 Viitanen 等[25]通过收集非匀质纸张试样断裂过程中的声发射(AE)信号以及利用散斑成像技术研究了在恒定外加应力和初始缺陷引起的蠕变断裂中试样失效的预测。 通过收集蠕变过程中的声发射信息以及利用散斑成像技术对蠕变寿命进行预测的结果分别如图6、 图7所示。 图6 中可以看到无论是利用声发射事件数N(t)还是声发射能量E(t)来预测蠕变寿命都表现出很大的随机性， 证明在远远超过依赖于样品的最小应变率之前， 使用间歇裂纹扩展的声发射进行预测是不可行的，而图7(b)中利用光学散斑分析技术得到的过程区长度阈值tthr,FPZ 与失效时间tc 大致呈正比，即由于断裂过程区的增长，可预测性是可能的。
图6 蠕变实验过程中的声发射事件数N(t)；蠕变实验过程中的声发射能量E(t)[25]
Fig.6 AE events N(t)over the creep experiment;AE energy E(t)over the experiments[25]
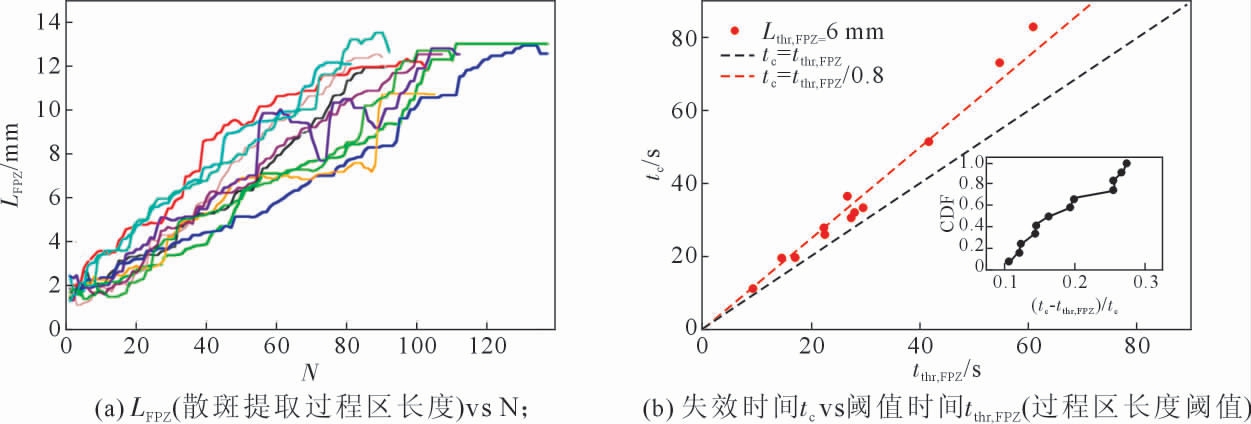
图7 LFPZ(散斑提取过程区长度)vs N；失效时间tc vs 阈值时间tthr,FPZ(过程区长度阈值)[25]
Fig.7 LFPZ vs N;Failure time tc vs threshold time tthr,FPZ for a process zone length threshold[25]
利用声发射(Acoustic Emission,AE)作为故障预测的诊断，通常是将断裂时所发出的信号作为“早期预警”[26]。通过声发射检测，裂纹扩展易于监测，具有极高的速度、精度。 但就目前的研究结果来看，通过声发射进行预测的效果并不理想， 主要因为声发射信号随机性较高，难以对断裂时刻进行准确预测，且声发射信号中携带的物理信息无法清晰辨别， 将其与机器学习进行结合或可实现更精准的预测[27]。
2 基于机器学习的蠕变寿命预测方法
最近， 数据驱动的机器学习方法已成功应用于材料性能预测、 新材料开发以及加深对材料现象的理解， 并证明了其在时间成本和预测性能方面的优越性， 机器学习成为揭示材料描述符和相关性能之间复杂关系的首选方法[28]。 机器学习不仅可以将不同合金的数据集迁移应用于目标合金， 而且可以将与蠕变高度相关的微观组织演化参数用作描述符，实现更精准的预测。迄今为止，机器学习在合金蠕变断裂寿命预测中的应用也已经取得了一定的进展。
早在十几年前，Venkatesh 和Rack 等[29]采用反向传播神经网络(Back propagation neural network,BPNN)(反向传播神经网络)预测Inconel 690 镍基单晶超合金在1 000 ℃和1 100 ℃下的蠕变断裂寿命。反向传播神经网络配置见图8。 两种温度下神经网络疲劳寿命的预测结果如图9。 基于统计设计训练集的反向传播神经网络技术，与改良的Coffin-Manson 法、 线性寿命分数法和滞后能量法相比，在1 000 ℃以及1 100 ℃时，模型的预测精度分别可达到100%和90%。
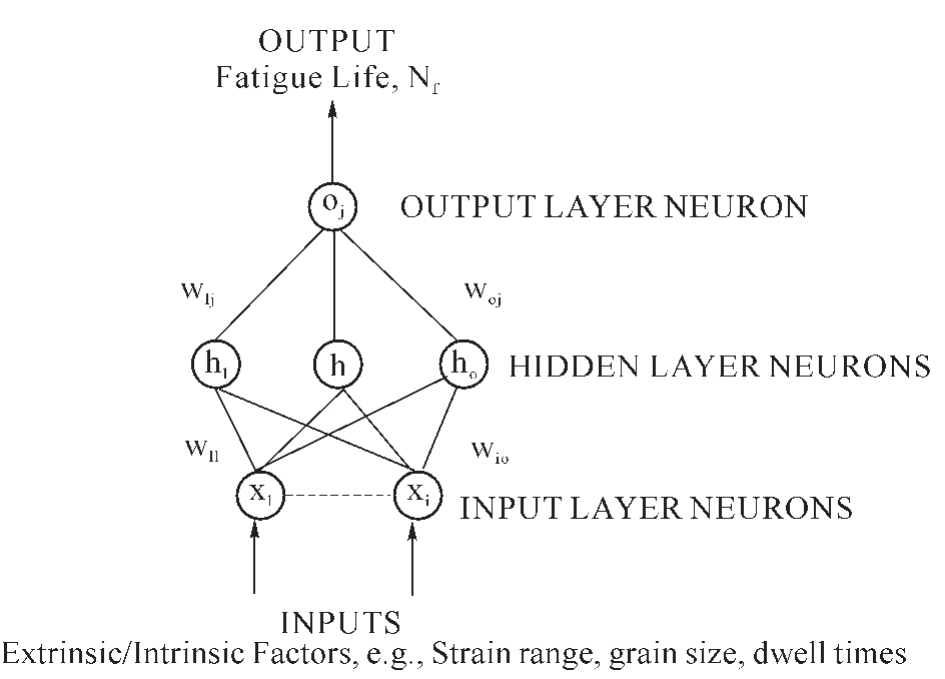
图8 典型反向传播神经网络配置[29]
Fig.8 Typical backpropagation neural network configuration[29]
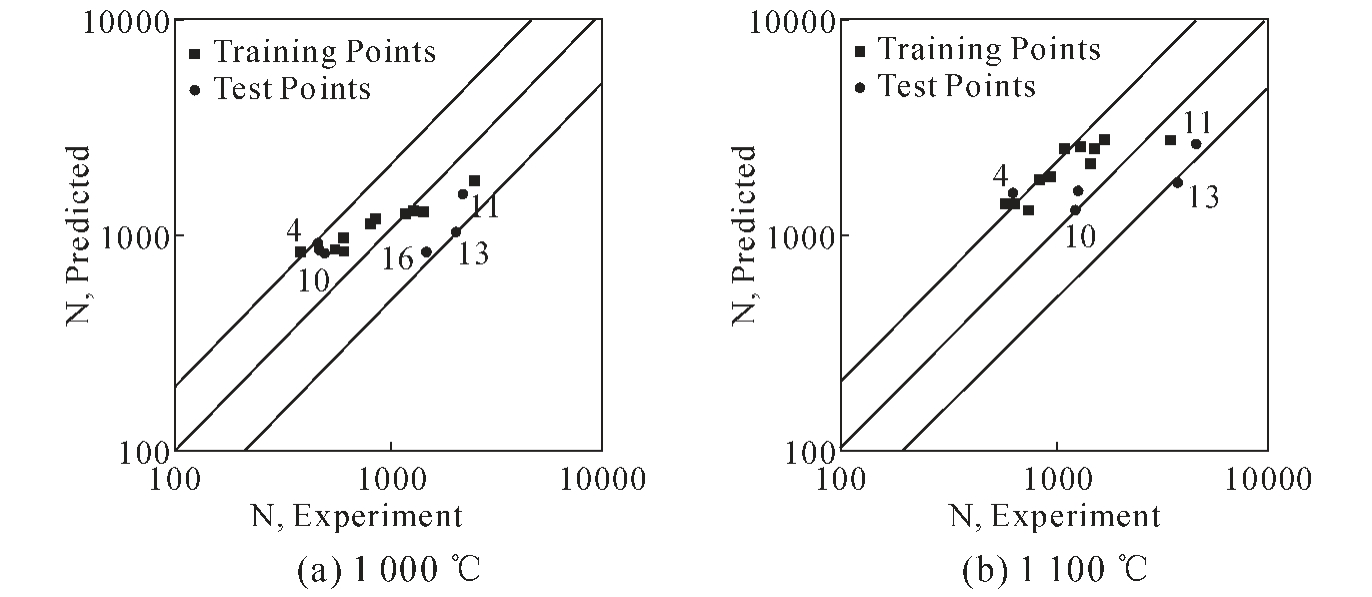
图9 1 000 ℃和1 100 ℃下的神经网络疲劳寿命预测结果[29]
Fig.9 Neural network fatigue life prediction results at 1 000 ℃and 1 100 ℃[29]
同样是利用神经网络，Yoo 等[30]利用贝叶斯神经网络(BNN)和马尔可夫链蒙特卡罗方法(MCMC)，使用相关材料描述符(包括化学成分、试验应力和试验温度)研究单晶高温合金蠕变性能的机理。预测结果如图10 所示，模型的预测精度达到93.2%。
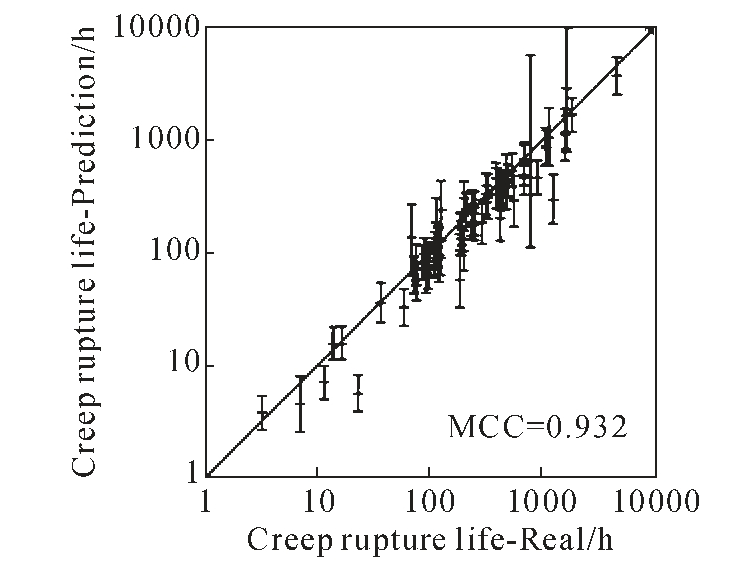
图10 数据的实际和预测蠕变断裂寿命[30]
Fig.10 Real and predicted creep rupture life for reserved data[30]
最近几年机器学习在蠕变寿命预测方面的应用飞速发展，Shin 等[6]使用高通量计算方法为高温合金生成新的热力学输入特征， 并基于Pearson 相关系数(PCC)和最大信息系数(MIC)分析所有输入特征与蠕变寿命之间的相关性， 重要性排序见图11。此外，作者根据特征重要性排序，选出不同数量特征描述符训练了包括随机森林(RF)，线性回归(LR)，最近邻(NN)，核岭回归(KR)，贝叶斯岭回归(BR)等模型。 证实应力(stress)和蠕变试验温度(T2)是对AFA合金蠕变性能影响最大的特征， 且该方法可扩展到除热力学以外的其他重要描述符。 Verma A K 等[31]使用多种机器学习方法， 包括线性回归、lasso 回归和t-分布随机邻域嵌入， 建立9E12 wt pct Cr 钢的加工/微观结构和蠕变性能之间的统计关系。高精度预测结果为在650 ℃和100 MPa 下蠕变寿命达到105 h 以上的新型马氏体钢的设计提供了参考。
图11 描述符重要性排序[6]
Fig.11 Importance ranking of descriptors[6]
Yue 等[7]将机器学习应用于镍基单晶高温合金材料的蠕变断裂寿命预测。 他们开发了一种分治自适应(DCSA)方法。 首先通过K 均值聚类算法，根据描述符自动将具有各种蠕变机制的合金样品分为若干集群； 然后为揭示不同集群中样品蠕变机制的差异，根据设计的适应度函数，每个集群从五种候选模型中自适应地选择最优模型， 以加速寿命预测。 此外，除基本描述符外，文中利用CALPHAD 方法及结构-性能关系， 计算并引入了能反映蠕变变形机制的5 个微观结构因子。 预测结果如图12。 该方法决定系数R2 达到0.917 6， 为蠕变寿命建立了有效的结构-性能关系， 为研究人员预测性能提供了新的视角。
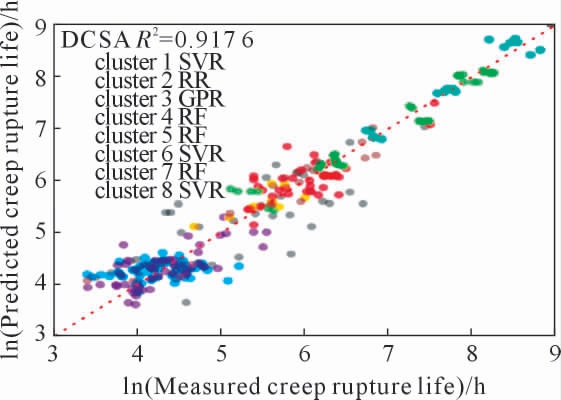
图12 DCSA 预测效果[7]
Fig.12 DCSA prediction effect[7]
前述采用机器学习对蠕变的断裂寿命进行预测的方法在预测精度和数据分析方面明显优于传统方法， 但是在有限的基于机器学习蠕变寿命预测研究中，大多数研究人员只分析了材料数据的统计关系，没有运用传统的蠕变研究。 基于此，Wang 等 [32]将TTP 方法与机器学习相结合， 探索了利用机器学习建立定量模型的想法， 以借助常规蠕变知识预测Cr-Mo 钢的蠕变寿命。 将目标特征(蠕变寿命)转换成3 个时间温度参数 (Larson-Miller 参数(LMP)、Manson-Haferd 参数（MHP)和Manson-Succop 参数(MSP))，使用皮尔逊相关系数(PCC)和斯皮尔曼相关系数(SCC)来讨论影响蠕变寿命的重要特征。 图13展示了4 种形式的目标特征的回归模型。如图所示，将蠕变寿命转化为LMP、MHP 和MSP 3 种参数，有效地提高了预测精度。图14 中特征重要性排序为专家分析影响Cr-Mo 钢蠕变性能的主要特征提供了新的见解且该研究成功地证明了将机器学习与时间-温度参数相结合预测蠕变寿命的可行性， 为研究人员预测钢的蠕变寿命提供了基本思路和工作流程。
图13 4 个目标特征的回归模型[32]
Fig.13 Models for four target features with the highest R2 score[32]
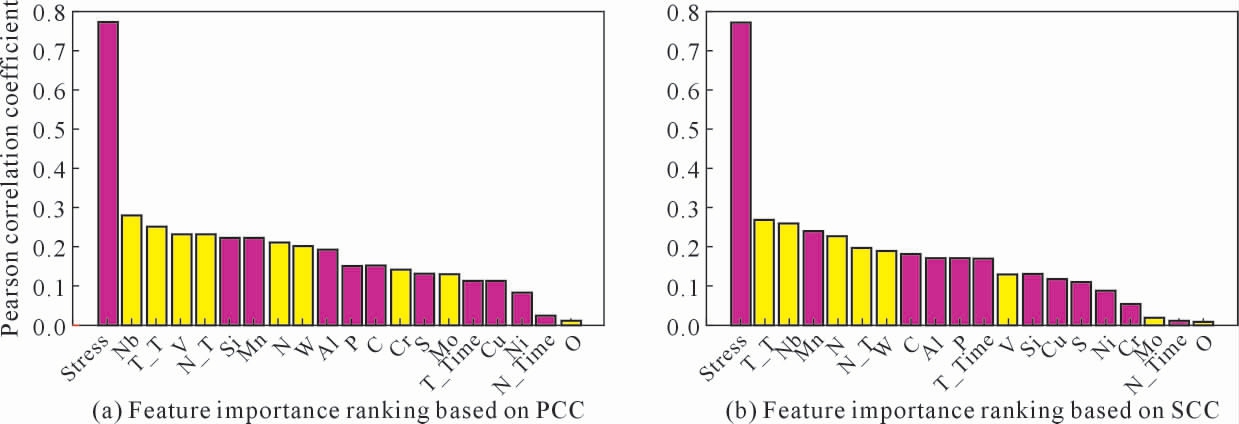
图14 基于相关性的特征重要性排序[32]
Fig.14 Feature importance ranking based on correlation[32]
前述利用声发射信号(AE)来预测蠕变寿命取得的效果并不理想，但随着失效的临近，损伤在空间上变得越来越相关， 而声发射信号在一定程度上可以代表损伤累积，其时空模式很可能反映这种相关性。然而，由于数据的高维性和相关性复杂，识别所述相关性以及由此产生的断裂前兆信号并不容易。 随着计算技术的发展， 人们开始采用基于AE 和机器学习(ML)的方法智能化识别损伤、研究其机理[27]。Biswas 等[33]使用监督机器学习来估计无序材料样本的剩余失效时间。 机器学习算法将无序材料蠕变损伤演化的中尺度弹塑性模型提供的时间信号作为输入， 从剪切样本的声发射时间序列评估故障的接近程度。 结果表明，对于较高的无序度，材料的可预测性相对较高，而对于更大的系统尺寸，材料的可预测性相对较低， 并提出在绝大多数情况下， 机器学习预测比文献中提出的其他预测方法表现得更好。
目前研究人员为了更快速、 更精准地对高温合金的蠕变断裂寿命进行预测，相继开发了多种基于机器学习的新预测方法，且很多都得到了较高的预测精度，但大多蠕变断裂无法完全阐明。 因此，利用机器学习等方法，合金的蠕变断裂强度仍有进一步研究的潜力[34]。
3 结论与展望
目前，对于蠕变断裂寿命的预测已经取得了显著的成果，很多对蠕变断裂寿命预测的研究已经达到了很高的预测精度，但总体上看仍然存在不足之处。 无论是采用传统基于理论计算的方法，还是应用机器学习对合金蠕变断裂寿命进行预测，均是围绕着初始材料特征信息进行预测， 例如成分信息、试验条件、工艺参数等，且大多预测的只是合金的最大蠕变断裂寿命，即便尝试通过收集断裂过程中的声发射(AE)信号对断裂的过程进行预测，得到的效果也并不算理想，还达不到精准预测蠕变断裂的断裂过程走向及曲线的效果。
长短期记忆网络 (Long Short-Term Memory,LSTM)是一种能够预测时间序列相关事件的时间循环神经网络，对于材料的研究而言，有望预测材料的响应曲线。 但是，目前该技术很少应用于材料的寿命预测领域。利用长短期记忆网络(LSTM)技术结合声发射手段，通过采集并分析材料响应过程中组织演化所释放的声信号，有望达到快速预测合金蠕变断裂行为或蠕变断裂曲线的目的。
[1] TANEIKE M, ABE F, SAWADA K. Creep-strengthening of steel at high temperatures using nano-sized carbonitride dispersions[J].Nature,2003,424:294-296.
[2] 陈传尧.疲劳与断裂[M].武汉: 华中科技大学出版社,2002.
[3] POLLOCK T M, TIN S. Nickel-based superalloys for advanced turbine engines:chemistry,microstructure and properties[J].Journal of Propulsion and Power,2006,22(2):361-374.
[4] 张力文，高珍鹏.304H 焊接接头高温蠕变疲劳行为研究及寿命预测[J].合成材料老化与应用,2021,2:60-63.
[5] CUI L,YU J,LIU J,et al.The creep deformation mechanisms of a newly designed nickel-base superalloy[J]. Materials Science and Engineering:A,2018,710:309-317.
[6] SHIN D,YAMAMOTO Y,BRADY M P,et al.Modern data analytics approach to predict creep of high-temperature alloys[J].Acta Materialia,2019,168:321-330.
[7] YUE L A, JW A, ZW B, et al. Predicting creep rupture life of Ni-based single crystal superalloys using divide-and-conquer approach based machine learning[J]. Acta Materialia, 2020, 195:454-467.
[8] DANG Y Y, ZHAO X B, YUAN Y, et al. Predicting long-term creep-rupture property of Inconel 740 and 740H[J].Materials at High Temperatures,2016,33(1):1-5.
[9] MARUYAMA K,ARMAKI H G,YOSHIMI K.Multiregion analysis of creep rupture data of 316 stainless steel[J].International Journal of Pressure Vessels and Piping,2007,84(3):171-176.
[10] BOLTON J.The potential for major extrapolation of creep rupture and creep strain data[J].Materials at High Temperatures,2014,31(2):109-120.
[11] BOLTON J. Extension of: Reliable analysis and extrapolation of creep rupture data[J].International Journal of Pressure Vessels and Piping,2019,172:348-359.
[12] KIM W G, YIN S N, LEE G G, et al. Creep oxidation behaviour and creep strength prediction for Alloy 617[J]. International Journal of Pressure Vessels&Piping,2010,87(6):289-295.
[13] MURAKAMI S.Notion of Continuum Damage Mechanics and its Application to Anisotropic Creep Damage Theory[J]. Journal of Engineering Materials＆Technology,1983,105(2)：99-105.
[14] MACLACHLAN D W, KNOWLES D M. Modelling and prediction of the stress rupture behaviour of single crystal superalloys[J].Materials Science&Engineering A,2001,302(2):275-285.
[15] FENG L, ZHANG K S, ZHANG G, et al. Anisotropic damage model under continuum slip crystal plasticity theory for single crystals[J].International Journal of Solids and Structures,2002,39(20):5279-5293.
[16] PRASAD S C, RAO I J, RAJAGOPAL K R. A continuum model for the creep of single crystal nickel-base superalloys[J].Acta Materialia,2005,53(3):669-679.
[17] PRASAD S C, RAJAGOPAL K R, RAO I J. A continuum model for the anisotropic creep of single crystal nickel-based superalloys[J].Acta Materialia,2006,54(6):1487-1500.
[18] VLADIMIROV I N, REESE S, EGGELER G. Constitutive modelling of the anisotropic creep behaviour of nickel-base single crystal superalloys[J]. International Journal of Mechanical Sciences,2009,51(4):305-313.
[19] AFEDELICH B,EPISHIN A,LINK T,et al.Experimental characterization and mechanical modeling of creep induced rafting in superalloys[J].Computational Materials Science,2012,64:2-6.
[20] KIM Y K, KIM D, KIM H K, et al. An intermediate temperature creep model for Ni-based superalloys [J]. International Journal of Plasticity,2016,79:153-175.
[21] LEOCMACH M,PERGE C,DIVOUX T,et al.Creep and fracture of a protein gel under stress[J].Physical Review Letters,2014,113(3):038303.
[22] LIN J, LERNER E, ROSSO A, et al. Scaling description of the yielding transition in soft amorphous solids at zero temperature[J].Proceedings of the National Academy of Sciences,2014,111(40):14382-14387.
[23] LEMA
TRE A. Structural relaxation is a scale-free process[J].Physical Review Letters,2014,113(24):245702.
[24] KOIVISTO J, OVASKA M, MIKSIC A, et al. Predicting sample lifetimes in creep fracture of heterogeneous materials[J]. Physical Review E,2016,94(2):023002.
[25] VIITANEN L,OVASKA M,RAM S K,et al.Predicting creep failure from cracks in a heterogeneous material using acoustic emission and speckle imaging[J]. Physical Review Applied, 2019, 11(2):024014.
[26] LENNARTZ-SASSINEK S,MAIN I G,ZAISER M,et al.Acceleration and localization of subcritical crack growth in a natural composite material[J].Physical Review E,2014,90(5):052401.
[27] MUIR C,SWAMINATHAN B,ALMANSOUR A S,et al.Damage mechanism identification in composites via machine learning and acoustic emission[J]. npj Computational Materials, 2021, 7(1):1-15.
[28] ZHANG M, SUN C N, ZHANG X, et al. High cycle fatigue life prediction of laser additive manufactured stainless steel: A machine learning approach[J].International Journal of Fatigue,2019,128:105194.
[29] VENKATESH V,RACK H J.Neural network approach to elevated temperature creep-fatigue life prediction[J]. International Journal of Fatigue,1999,21(3):225-234.
[30] YOO Y S,JO C Y,JONES C N.Compositional prediction of creep rupture life of single crystal Ni base superalloy by Bayesian neural network [J].Materials Science&Engineering A, 2002, 336(1-2):22-29.
[31] VERMA A K,HAWK J A,BRUCKMAN L S,et al.Mapping Multivariate Influence of Alloying Elements on Creep Behavior for Design of New Martensitic Steels[J].Metallurgical and Materials Transactions A,2019,50(7):3106-3120.
[32] WANG J, FA Y, TIAN Y, et al. A machine-learning approach to predict creep properties of Cr-Mo steel with time-temperature pa rameters[J].Journal of Materials Research and Technology, 2021,13:635-650.
[33] BISWAS S, FERNANDEZ CASTELLANOS D, ZAISER M. Prediction of creep failure time using machine learning[J].Scientific Reports,2020,10:16910.
[34] HE L, WANG Z L, AKEBONO H, et al. Machine learning-based predictions of fatigue life and fatigue limit for steels[J].Journal of Materials Science&Technology,2021,31:9-19.