Cu-Sn 合金俗称青铜,是人类使用最早的合金之一,Sn 的添加使得合金材料具有良好的弹性、耐磨性、抗磁性及耐腐蚀性,可在冷态和热态进行机械和压力加工,并且易于进行塑性变形和焊接,切削性较好,在大气和淡水、海水中抗蚀性良好,主要用于接触线以及各种弹性元件、管配件、化工器械、耐磨零件和抗磁零件等[1-4]。但是通过传统铸造方法生产的Cu-Sn 合金具有严重的偏析现象,而上引连铸具有较大冷却强度,可以有效缩短固液相区凝固时间,从而减少偏析,同时能够连续化制备,主要有3 种加工工艺:上引连铸-冷轧法、上引连铸连续挤压法[5]以及连铸连轧-拉拔法[6]。
随着电子器件小型化、便携化的发展趋势对Cu-Sn 合金的铸坯质量与加工性能提出了更高要求。这两项指标与晶粒尺寸、取向及分布密不可分。作为有效提升合金材料综合性能的手段,铸件晶粒组织调控成为当前研究热门,但有关Cu-Sn 合金凝固组织模拟的研究报道尚不多见。目前主流微观组织仿真模拟方法有3 种:蒙特-卡罗(Monte Carlo MC method)法,相场法(Phase field method)以及元胞自动机(cellular automata,CA)法。
1 微观组织仿真模拟方法
1.1 相场法
相场模型是一种建立在热力学基础上综合有序化势与热力学驱动力共同作用而建立的用于描述系统演化动力学的模型。20 世纪80 年代,Collins[7]、Caginalp[8]最早提出相场模型,于1994 年Kobayashi[9]首先利用相场法实现纯金属过冷溶体中枝晶生长的二维仿真模拟。Avila-Davila[10]等人运用相场法对等温时效下的Cu-Ni 系合金进行了自旋分解组织模拟数值模拟和实验。Long[11]等人建立三元合金自旋节分解的相场模型,对等温时效过程中Cu-Ni-Si 的旋转分解组织进行仿真模拟。
1.2 MC 法
MC 法作为一种随机性模型方法,广泛应用于材料中的随机过程以及随机现象,包括薄膜长大、扩散与相变以及凝固过程晶粒生长等。1984 年Srolovitz、Anderson [12]等人最早提出图形蒙特卡罗法用于模拟凝固过程中微观组织演化。20 世纪80年代末,Spittle[13]与Brown[14]率先将MC 运用到合金凝固组织模拟中,分别得出小铸件等轴晶的形成主要机制是非均质形核,当柱状界面的等轴晶体积分数达到50%时,开始发生柱状晶向等轴晶转变。Baibuz[15]等人通过动力学蒙特卡罗(Kinetics Monte Carlo)法计算得到Cu 自扩散的迁移壁垒数据。
1.3 CA 法
20 世纪80 年代开始,一些学者逐渐提出将CA 法应用于凝固模拟,用元胞自动机法揭示金属凝固过程。CA 方法是确定性模型与随机性模型的结合体,其直径尖端动力学生长速率是基于物理理论的确定性模型,而形核分布与晶粒取向采用随机性模型。因此,CA 方法在吸收MC 法长处的同时,在晶体效应和晶粒选择上也具有物理意义。1993 年Rappaz、Gandia[16]率先将CA 法用于合金凝固仿真模拟,并于1994 年将元胞自动(CA)法与有限元法FE(Finite element)进行耦合,结合高斯分布的连续形核模型,对Al-Si 晶粒结构进行仿真模拟 [17]。Wang [18] 运用CA-FE 模型演化Cu-10Al 热型连铸过程中晶粒结构变化,再现了在连铸过程中晶粒由等轴晶向柱状晶的转变。王松[19]等人采用CA-FE 法对Cu-Cr-Zr-Ag 在3 种冷却条件下凝固过程不同阶段显微组织,成功的预测了铸件内部晶粒形状与其分布。
由于CA-FE 法结合随机方法、确定性方法的优点,基于形核的物理机制和枝晶生长动力学,能有效预测铸件凝固过程中晶粒生长取向以及尺寸,因此本研究采用CA-FE 法预测模拟Cu-0.3Sn 合金在上引连续铸造工艺中通过改变铸造温度、铸造速度其宏观温度场与微观晶粒组织演变过程,讨论不同铸造参数对合金凝固过程中S/L 界面以及晶粒形貌的影响规律。
2 数学模型及参数选取
2.1 宏观温度场模型
宏观数值模拟模型基于Navier—Stokes 方程,采用焓处理凝固过程中合金元素结晶相变[20-21]。公式(1)、(2)、(3)、(4)分别包含了质量、动量及能量的金属熔体三维瞬时流动和传热过程。在实际铸造过程中伴随重力作用,因此公式中加入重力项,同时将此方程代入标准的动量方程中,合金液凝固过程中的固相区、糊状区也可以运用此控制方程。
(1)质量守恒方程
(2)动量守恒方程(以x 方向为例,y、z 方向类似)
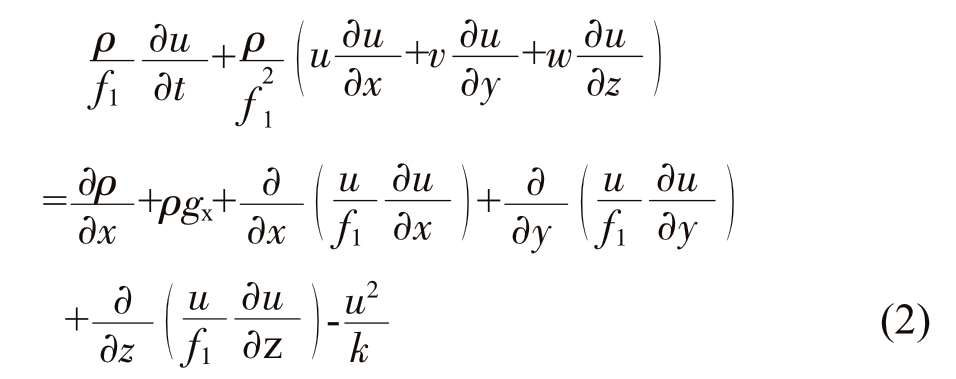
(3)能量守恒方程
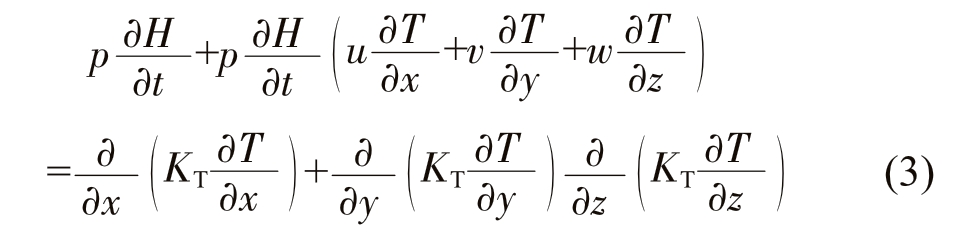
其中,
式中,u、v、w 为x、y、z 方向上的速度分量,m/s;f1、f2为液、固相率;P 为压力,Pa;gx 为x 方向上重力分量,m/s2;ρ 为密度,kg/m3;u 为渗透率,m2;Cp 为比热容,J·kg-1·℃-1;H 为热焓,J/mol;L 为凝固潜热,J/kg。
2.2 形核模型
形核是凝固过程中组织演变的基础及主导阶段,是最终晶粒组织形成的关键。分为两种均质形核与非均质形核,根据上述理论本研究采用非均质成核模型。在非均质形核时,于合金熔体内不同位置发生形核,这些位置可以通过dn/d(ΔT)来描述[22-23]:
式中,ΔT 为过冷度,K;ΔTmax 为平均形核过冷度,K;ΔTσ为形核过冷度标准方差,K;nmax 为最大形核密度,m-3。
当给定过冷度时,晶核密度n(ΔT)可由下式分布曲线的积分求得[24]:
实际凝固过程中,铸件中心和表面的形核相差较大,需采用两套形核参数,即体形核参数(ΔTv,max平均体形核过冷度,ΔTv,σ 平均体形核标准方差以及nv,max 体形核密度)和面形核参数(ΔTs,max 平均面形核过冷度,ΔTs,σ 平均面形核标准方差以及ns,max 面形核密度)。形核参数是通过理论分析和实验相结合估算得出的。体与面的非均匀形核通过高斯分布函数来描述(见图1),体形核参数单位和面形核参数单位分别为:m-3、m-2。
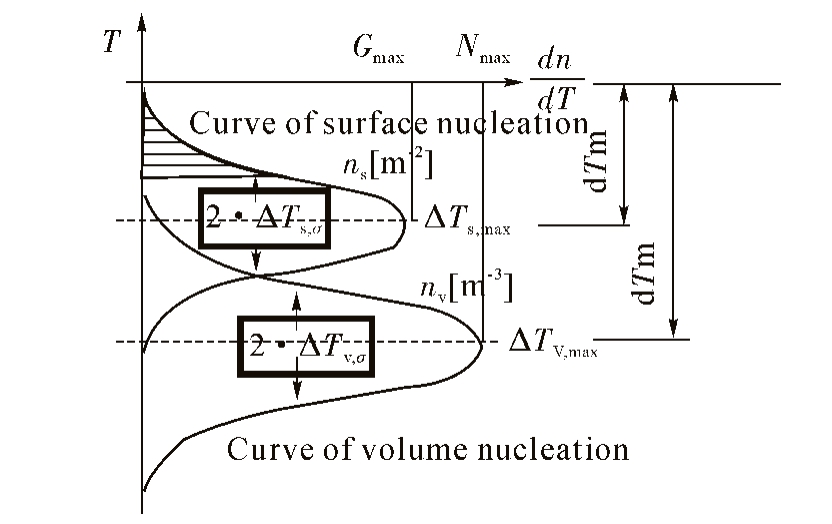
图1 体和面非均匀形核的高斯分布曲线
Fig.1 Guass distribution of volume and surface heterogeneous nucleation
2.3 枝晶尖端动力学生长模型
根据凝固理论,晶粒生长是由于枝晶前沿存在过冷熔体,同时受到动力学过冷和成分过冷的共同影响[25-26]。枝晶尖端总过冷度ΔT 是以下4 个过冷度的总和。
式中,ΔTc 为成分过冷度;ΔTt 为热力学过冷度;ΔTr为固-液界面曲率过冷度;ΔTk 为生长动力学过冷度,单位均为K。
绝大部分金属在正常凝固条件下,相对于成分过冷,其它3 个过冷度均可以忽略不计,则式(7)可近似为ΔT=ΔTc。Kurz [27] 等人提出的KGT (Kurz-Giovanola-Trivedi)模型可用来模拟凝固时枝晶生长过程。为加快计算速度,Rappaz 和Kurz 简化了KGT 模型中v 与ΔT 之间的关系并进行拟合,得到以下公式:
式中,a2、a3 为枝晶前沿动力学生长系数,可通过公式(9)、(10)求出:
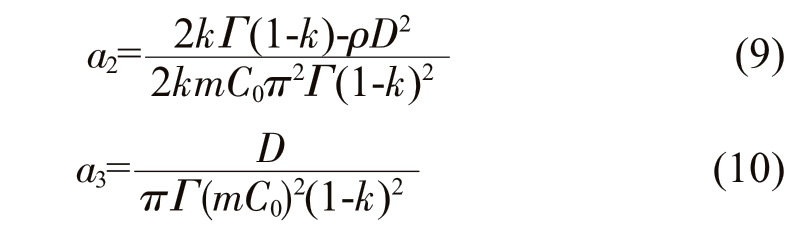
计算所得,a2=8.928 534×10-6,a3=4.057 223×10-4。
2.4 模拟参数选取
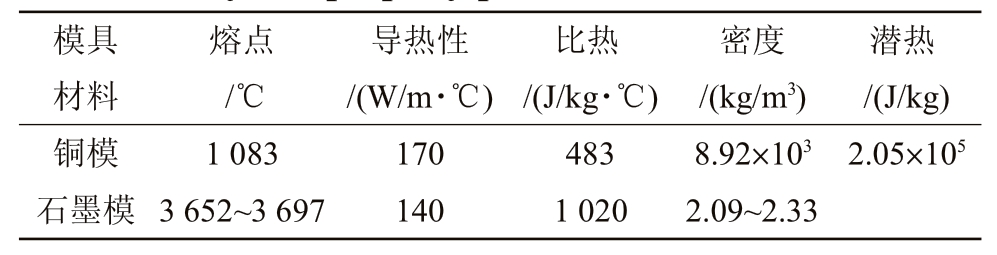
本研究温度场采用混合欧拉—拉格朗日算法(Mixed Lagrangian-Eulerian algorithm)进行仿真计算,其原理如图2(a)所示。整个计算模型分为5 部分,1为石墨结晶器,2 为水冷铜套,3 为纯铜引杆,4 为提供金属液部分,5 为与引杆接触的铜液,6 为扯叠层。本研究连铸计算模型如图2(b)所示,(b)中Ⅰ、Ⅱ、Ⅲ与(a)中1、2、3 对应,模型网格大小为1 mm,网格总数为1 131 887,其中面网格数为98 855,体网格为1 033 032,模具材料物理参数如表1。
表1 模具材料物理性质参数
Tab.1 Physical property parameters of die materials
?
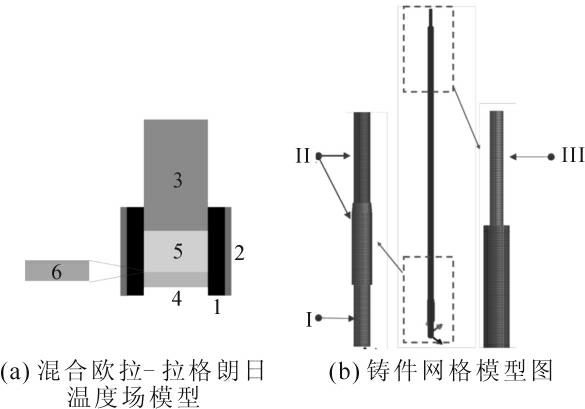
图2 凝固模型示意图
Fig.2 Schematic solidification model
通过实验测得Cu-0.3Sn 合金液相线TL 为1 356 K,TS 为1 180 K。数值计算中合金材料物理性质随温度变化曲线如图3。此外,3D—CAFÉ 模型直径尖端动力学生长系数根据液相线斜率、溶质平衡分配系数以及扩散系数求得a2=8.928 534×10-6,a3=4.057 223×10-4。面、体形核参数可根据ASTM(American Society of Testing Materials)标准最大形核密度计算公式![]() (NV 为单位体积晶粒数,NA 为单位面积晶粒数,NL 单位测量线上晶粒数)计算,也可通过文献调研获得。本研究采用体形核密度nv,max=3.0×108,ns,max=5×106。根据实验凝固组织,通过数值模拟调整形核参数,最终形核参数见表2。
(NV 为单位体积晶粒数,NA 为单位面积晶粒数,NL 单位测量线上晶粒数)计算,也可通过文献调研获得。本研究采用体形核密度nv,max=3.0×108,ns,max=5×106。根据实验凝固组织,通过数值模拟调整形核参数,最终形核参数见表2。
表2 上引连铸过程微观模拟参数
Tab.2 Micro simulation parameters of upward continuous casting process

?
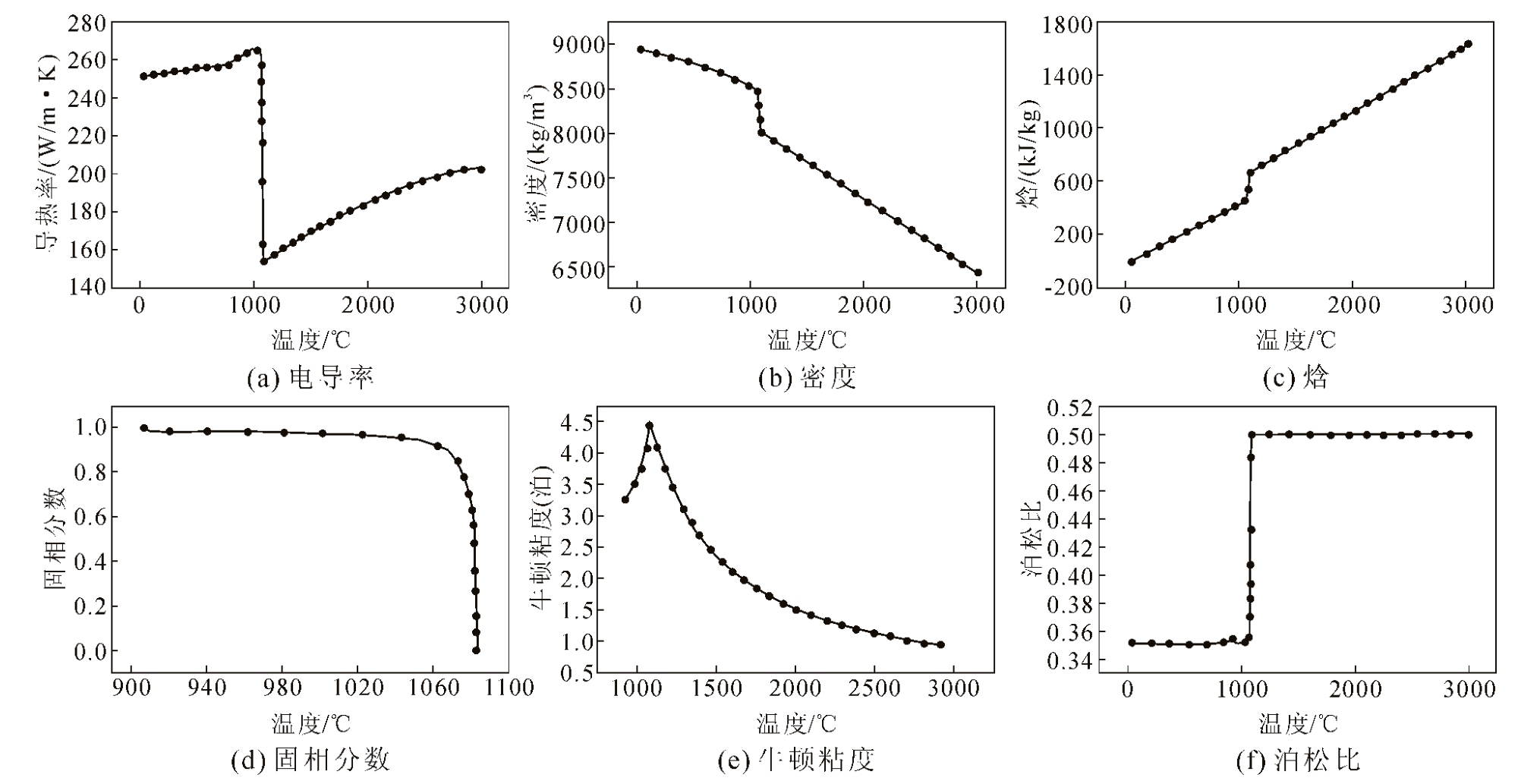
图3 材料物理性质随温度变化曲线
Fig.3 Variation curve of material physical properties with temperature
边界条件参数合理性决定了模拟的正确性,在本研究过程中宏观温度场主要受两个换热条件影响,铸件—石墨结晶器界面换热系数与一冷区内水冷强度。根据文献调研[28],铸件—结晶器界面换热系数取2 500 W/(m2·K)。水冷强度可根据下式计算:
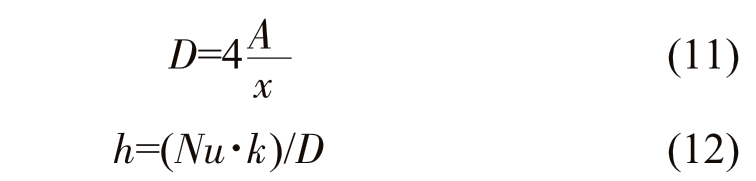
冷却水通道为环状管道,故公式(11)则变为:
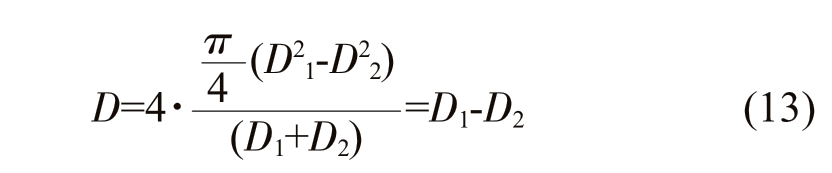
式中,D 为液压直径,A 为定义管道截面积,x 为管道湿润周,D1、D2 分别为环状管道的两个直径。计算得到水冷强度为5.525 3×103 W/(m2·K)。
3 实验
图4 为上引连铸铸造示意图。首先在连铸炉坩埚内放入50 kg 纯度为99.9%铜杆,调节电流为40~50 A对坩埚进行预热烘烤,后间隔30 min 调节一次电流至110 A,步长为20 A/次。待Cu 杆熔化后,加入定量锡粒。调节电流保温,间隔5 min 测温一次,使铸造温度为稳定在1 150、1 200、1 250 ℃(±10 ℃)。温度达到后调节铸造速度为1、3、5 mm/s,调节工艺时,停止铸造一分钟后继续铸造。对不同工艺的杆材选取位置将铸件切割成20 mm 的纵截面并镶入环氧树脂模块中,进行研磨、抛光和腐蚀蚀刻30 s,使晶粒、晶界清晰可见。使用ADSM301 安东星Andonstar 数码显微镜进行金相拍摄,根据GB/T 6394-2017《金属平均晶粒度测定法》[29]测定截面平均晶粒面积。
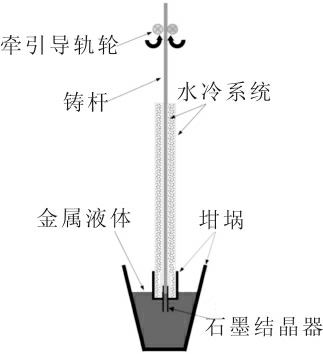
图4 上引连铸铸造示意图
Fig.4 Schematic upward continuous casting
表3 上引连铸实验参数
Tab.3 Experimental parameters of upward continuous casting

?
4 结果和讨论
4.1 仿真模拟结果与验证
4.1.1 宏观温度场
图5、图6 分别为1 150、1 200、1 250 ℃3 个温度,不同铸造速度下合金杆材经过一冷区出口温度以及宏观温度场温度分布云图。在实际实验过程中,在不同温度不同铸造速度下,通过红外测温设备测得铸坯一冷区出口温度稳定在31~32 ℃,不会因为铸造温度的升高以及速度提高变化而明显变化,模拟中温度为31 ℃,验证温度场模拟的合理性。

图5 不同铸造温度下,合金杆材出口温度随速度变化图
Fig.5 Variation of outlet temperature of alloy rod with speed at different casting temperatures
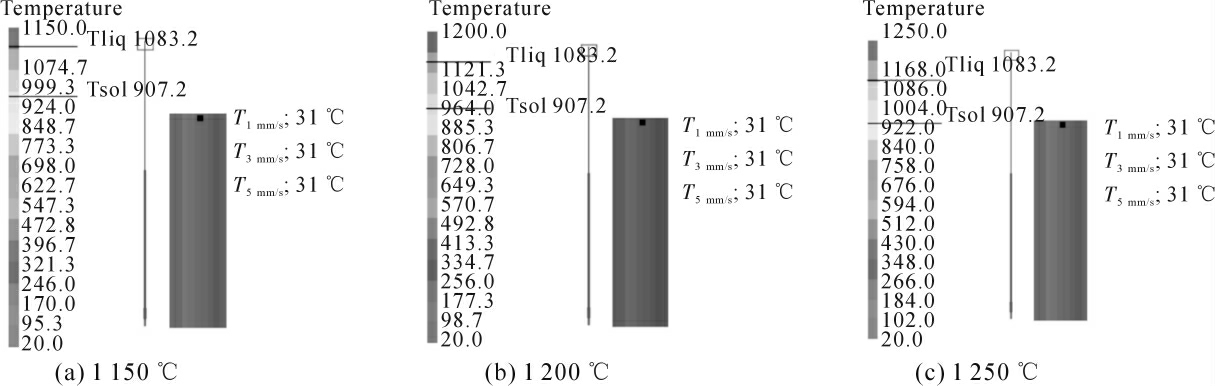
图6 不同铸造温度下,合金杆材随速度变化温度云图
Fig.6 Temperature nephogram of alloy rod with speed under different casting temperatures
4.1.2 S/L(固/液)界面形状及深度
图7 为1 150、1 200、1 250 ℃3 个温度,不同铸造速度下S/L 界面变化图。图8 为不同铸造温度下S/L 界面深度及S/L 界面温度梯度随铸造速度变化曲线。结合图7、图8,相同铸造速度下,铸造温度对S/L 界面形状、深度及界面温度梯度影响较小。如当铸造速度为1 mm/s 时,1 150 、1 200 、1 250 ℃3个温度下的S/L 界面基本维持平面状,深度分别为1.4、1.5、2.0 mm,温度梯度为5.0、5.4、6.7 K;但是,当温度固定改变铸造速度时,S/L 界面随着速度的增加由原先近似直线状开始隆起,呈尖锐山峰状。如当铸造温度变为1 150 ℃时,S/L 界面由铸造速度为1 mm/s时的平面状变为5 mm/s 的窄梨形。此时1、3、5 mm/s 3 个铸造速度下对应的S/L 界面深度分别为1.6、2.8、6.0 mm,温度梯度分别为5.0、5.4、6.7 K。
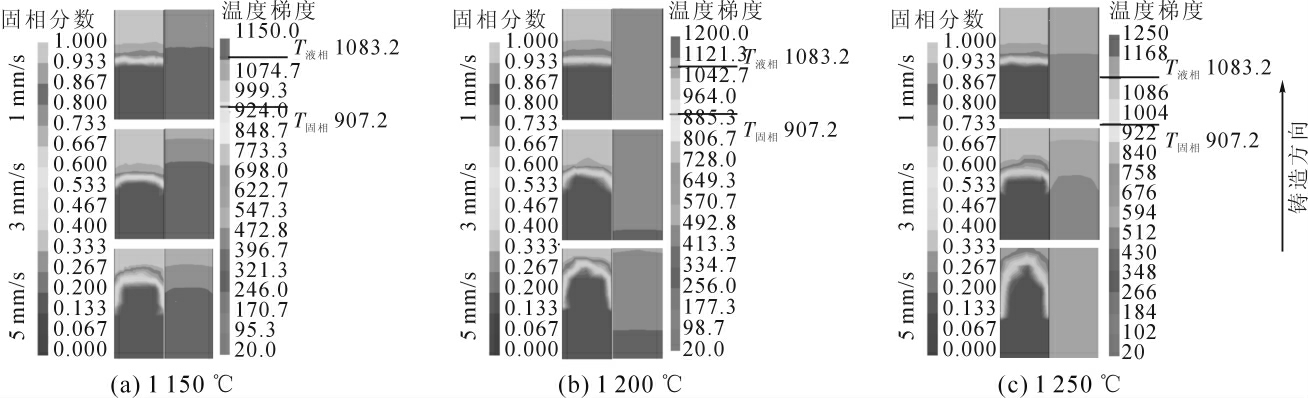
图7 不同铸造工艺下S/L 界面变化图
Fig.7 Variation of S/L interface under different casting processes
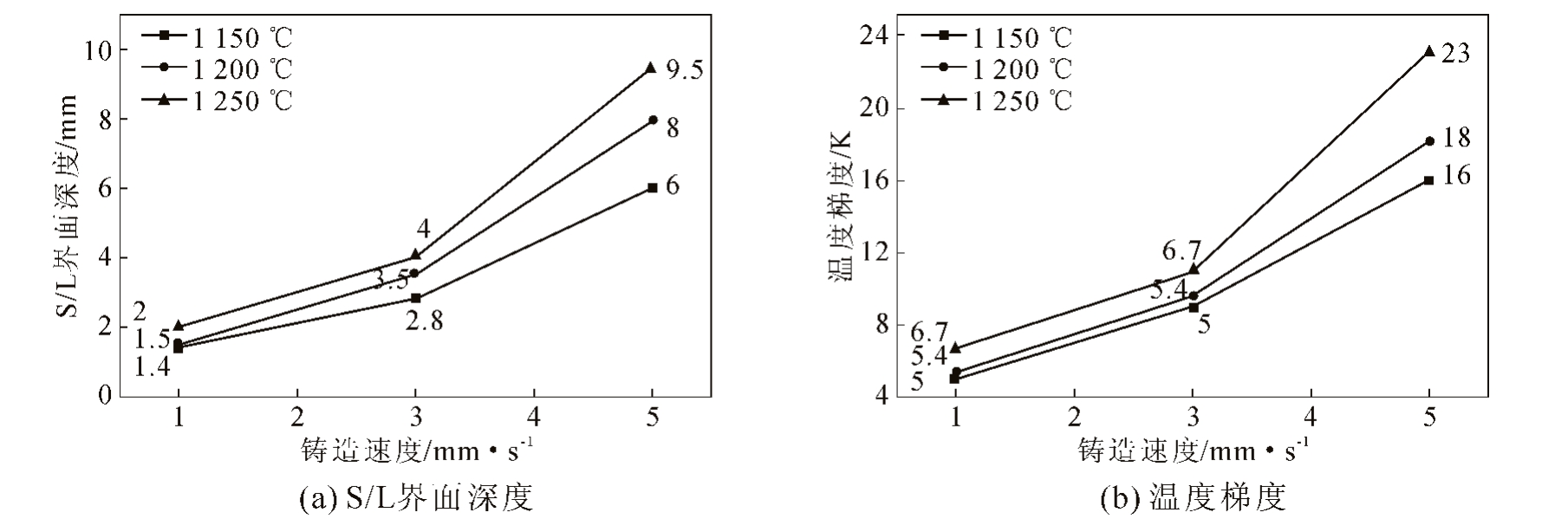
图8 不同铸造工艺下S/L 界面深度及温度梯度随铸造速度变化曲线
Fig.8 Variation curves of S/L interface depth and temperature gradient with casting speed under different casting processes
4.1.3 微观凝固组织
图9不同铸造温度、速度下实验与模拟微观晶粒组织对比图。S/L 界面及深度随着温度和速度的提升而尖锐,晶粒生长方向与S/L 界面密切相关,当铸造速度为1 mm/s,根据图7,S/L 界面基本保持平面,此时晶粒组织生长方向以轴向为主;当速度为3 mm/s 时,浇铸温度开始影响S/L 界面,微微凸起,此时晶粒组织生长方向虽仍以轴向为主,但是出现径向生长趋势,但是随着温度升高,晶粒径向生长驱动力减弱;当铸造速度提高到5 mm/s 时,S/L 界面凸起,呈窄梨形,晶粒生长方向为轴向、径向混合方式生长。

图9 不同铸造温度、速度下杆材晶粒组织变化云图
Fig.9 Nephogram of grain structure change of rod under different casting temperature and speed
图10 为铸态晶粒组织尺寸对比图。从图10 可以看出,相较于铸造速度,铸造温度对晶粒尺寸影响更小,如铸造速度为1 mm/s,此时1 150、1 200、1 250 ℃晶粒尺寸分别为40.32、28.51、20.16 mm2;当温度为1150 ℃时,1、3、5 mm/s 晶粒尺寸分别为20.16、2.53、1.78 mm2。
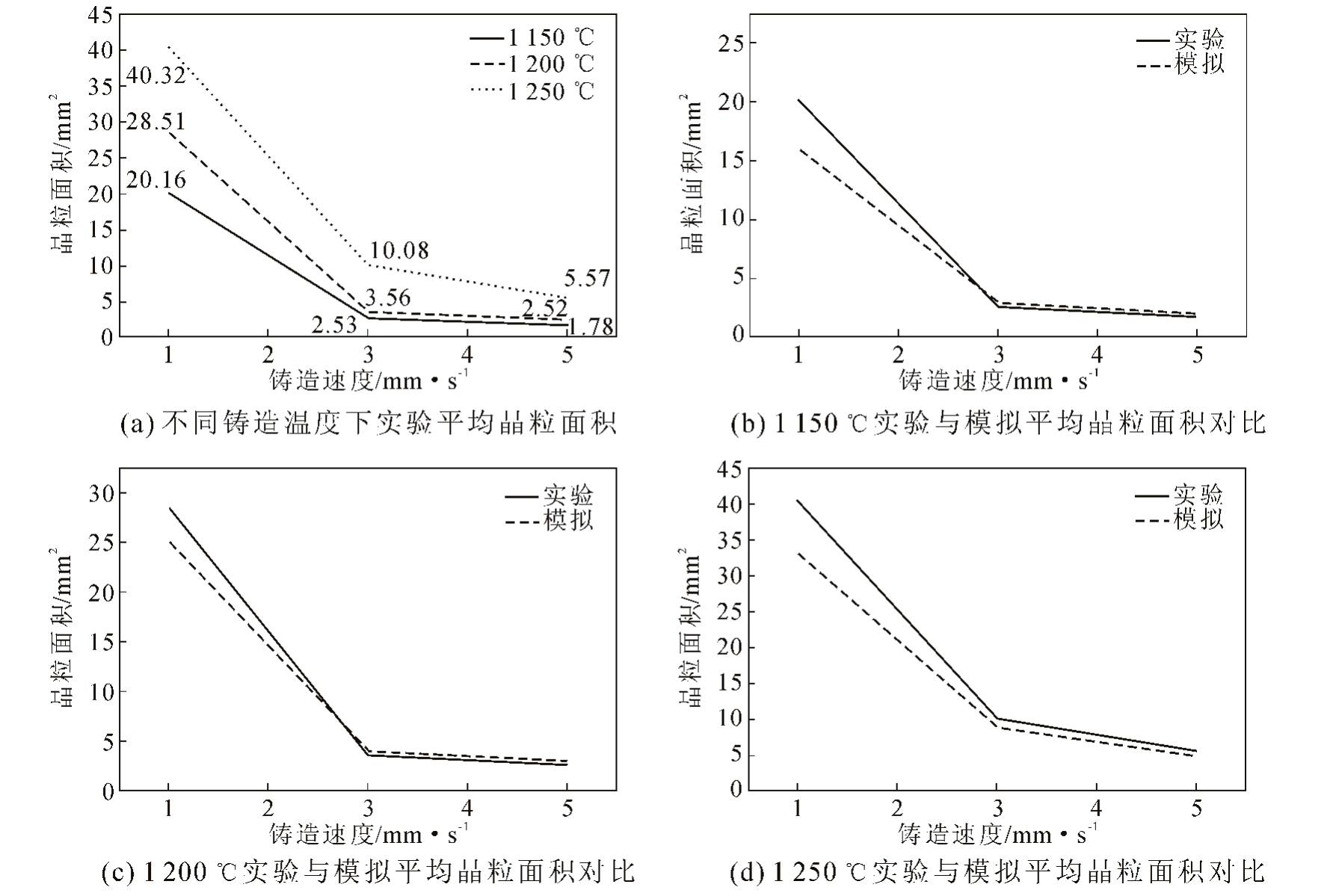
图10 平均晶粒面积变化示意图
Fig.10 Variation of average grain area
4.2 形状因数
图11 为水冷强度为5.525 3×103 W/(m2·K)下铸造速度、铸造温度、S/L 界面深度3 个参数非线性曲面拟合结果。表达式为见公式(14),引入一个形状因子ξ,它定义了Cu-0.3Sn 合金杆材S/L 界面的形状和与铸速、铸造温度、水冷强度的关系。
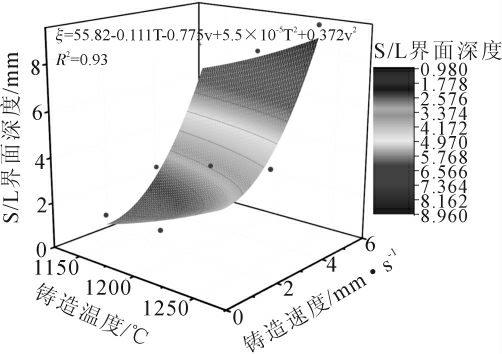
图11 水冷强度为5.525 3×103W/(m2·K)下S/L 界面深度拟合结果
Fig.11 Water cooling intensity is fitting results of S/L interface depth at 5.525 3×103 W/(m2·K)
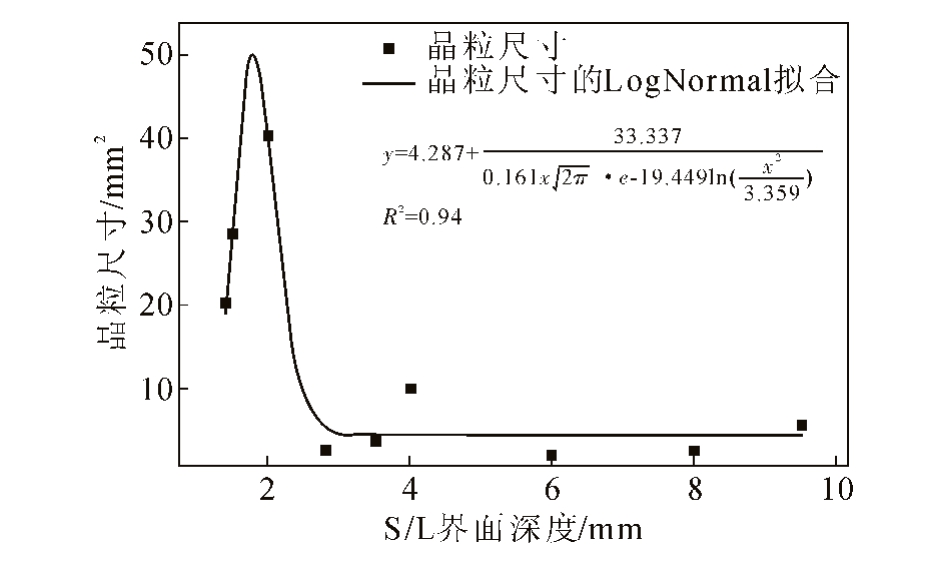
图12 S/L 界面深度与晶粒尺寸拟合图
Fig.12 Fitting diagram of S/L interface depth and grain size
其中,T 为铸造温度;v 为铸造速度;H 为水冷强度。其方差R2=0.91。
同时对S/L 界面深度及晶粒尺寸进行对数正态分布拟合如图11,晶粒尺寸与S/L 界面深度满足公式(15),其方差R2=0.94
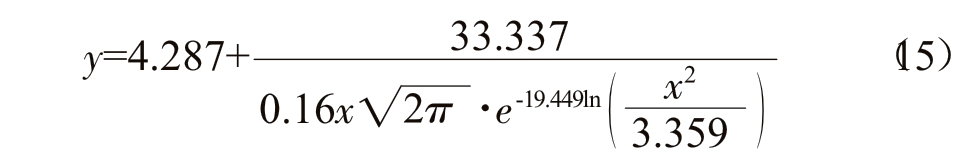
通过公式(14)、(15)使得低含量第二合金元素铜合金在上引连续铸造前通过对铸造工艺的确定计算出S/L 界面大致形状及深度,以及对应的平均晶粒尺寸,对铸造工艺进行指导。
5 结论
(1)采用混合欧拉-拉格朗日算法对不同铸造温度、不同铸造速度下Cu-Sn 合金杆材温度场进行模拟仿真,与试验结果基本一致。
(2)采用CA-FE 方法对不同条件下合金杆材微观晶粒组织进行仿真模拟。当铸造速度增加时,晶粒由轴向生长变为轴向-径向混合生长,随着温度的升高晶粒变得粗大。
(3)讨论不同铸造温度、速度以及水冷强度对S/L 界面深度的影响,得出一般公式,对S/L 界面深度与晶粒尺寸进行拟合得出公式。
(4)Cu-Sn 合金凝固组织模拟所选模型及参数设置的合理性,可为进一步优化铸造工艺参数提供一定依据,也为其他合金提供参考。
[1] ZHANG M, ZHANG Z, ZHAO Z, et al. Tunable Selectivity for Electrochemical CO2 Reduction by Bimetallic Cu-Sn Catalysts:Elucidating the Roles of Cu and Sn[J].ACS Catalysis,2021,11(17):11103-11108.
[2] LYU Y, CAI M, LIU S, et al. Cu-Sn low-temperature stack bond ing for 3D packaging[C]//2013 14th International Conference on Electronic Packaging Technology.IEEE,2013.84-87.
[3] RAJ R, SHRIVASTAVA P, JINDAL N, et al. Development and characterization of eutectic Sn-Zn,Sn-Ag,Sn-Bi and Sn-Cu solder alloys [J]. International Journal of Materials Research, 2019, 110(12):1150-1159.
[4] HANG C, TIAN Y, ZHANG R, et al. Phase transformation and grain orientation of Cu-Sn intermetallic compounds during low temperature bonding process[J].Journal of Materials Science:Materials in Electronics,2013,24(10):3905-3913.
[5] 庄楠,袁远,潘利科,等.Cu-Sn 合金接触线孔洞缺陷分析[J].铁道技术监督,2020,48(10):3.
[6] 杨运川.SCR 连铸连轧法制备Cu-Sn 接触线工艺及Sn 对组织和性能的影响[J].材料导报,2012,26(1):86-89.
[7] COLLINS J B, LEVINE H. Diffuse interface model of diffus ion-limited crystal growth[J]. Physical Review B, 1985, 31(9):6119.
[8] CAGINALP G, FIFE P C. Dynamics of layered interfaces arising from phase boundaries[J].SIAM Journal on Applied Mathematics,1988,48(3):506-518.
[9] KOBAYASHI R.Modeling and numerical simulations of dendritic crystal growth [J]. Physica D: Nonlinear Phenomena, 1993, 63(3-4):410-423.
[10] Avila-Davila E O,Melo-Maximo D V, Gutierrez-Mendez C, et al.Numerical simulation of microstructural evolution in isothermal ly-aged Cu-Ni based alloys [C]//Advanced Materials Research.Trans Tech Publications Ltd,2007.672-677.
[11] LONG Y Q,LIU P,LIU Y,et al.Numerical Simulation of Spinodal Deposition in Cu-6at.%Ni-3at.%Si Ternary Alloy Using of Phase Field Method [J]. Materials Science Forum, 2011, 704-705(12):1410-1415.
[12] ANDERSON M P,SROLOVITZ D J,GREST G S,et al.Computer simulation of grain growth—I. Kinetics[J]. Acta metallurgica,1984,32(5):783-791.
[13] SPITTLE J A, BROWN S G R. A computer simulation of the influence of processing conditions on as-cast grain structures[J].Journal of Materials Science,1989,24(5):1777-1781.
[14] BROWN S G R, SPITTLE J A. Computer simulation of grain growth and macrostructure development during solidification[J].Materials Science and Technology,1989,5(4):362-368.
[15] BAIBUZ E, VIGONSKI S, LAHTINEN J, et al. Data sets of migration barriers for atomistic Kinetic Monte Carlo simulations of Cu self-diffusion via first nearest neighbour atomic jumps[J].Data in Brief,2018,17:739-743.
[16] RAPPAZM,GANDINCA.Probabilisticmodellingof microstructure formation in solidification processes [J]. Acta metallurgica et materialia,1993,41(2):345-360.
[17] GANDIN C A, RAPPAZ M. A coupled finite element-cellular automaton model for the prediction of dendritic grain structures in solidification processes[J]. Acta Metallurgica et Materialia, 1994,42(7):2233-2246.
[18] WANG Z, LUO S, WANG W, et al. Numerical Simulation of Solidification Structure of Continuously Cast Billet with Grain Motion[J]. Metallurgical and Materials Transactions B, 2020, 51(6):2882-2894.
[19] 王松,谢明,王塞北,等.基于CA-FE 法的Cu—Cr-Zr-Ag 合金凝固组织模拟[J].贵金属,2013,34(3):50-54.
[20] NASTAC L.Modeling and Simulation of Microstructure Evolution in Alloys[M].New York:Kluwer Academic,2004.
[21] JABUR A S, JALIL J M, TAKHAKH A M. Experimental Investigation and Simulation of Al-Si Casting Microstructure Formation[J].Arabian Journal for Science and Engineering,2012,37(3):777-792.
[22] 胡庚祥,蔡洵,戎咏华.材料科学基础[M].上海:上海交通大学出版社,2010.
[23] MARTORANO M D A, BISCUOLA V B. Predicting the columnar-to-equiaxed transition for a distribution of nucleation undercoolings[J].Acta Materialia,2009,57(2):607-615.
[24] BAI L, WANG B, ZHONG H, et al. Experimental and numerical simulations of the solidification process in continuous casting of slab[J].Metals,2016,6(3):53.
[25] LIU D R,YANG Y,SUN Q Y,et al.2D cellular automaton-finite element simulation of grain structure and macrosegregation during solidification of Al-4wt% Cu Alloy[J]. International Journal of Cast Metals Research,2016,29(6):393-402.
[26] WANG J, WANG F, ZHAO Y, et al. Numerical simulation of 3D-microstructures in solidification processes based on the CAFE method [J]. International Journal of Minerals, Metallurgy and Materials,2009,16(6):640-645.
[27] KURZ W,GIOVANOLA B,TRIVEDI R.Theory of microstructural development during rapid solidification [J]. Acta metallurgica,1986,34(5):823-830.
[28] 潘德清. Cu-15Ni-8Sn 合金圆锭的连续铸造成形研究[D].广东:华南理工大学,2020.
[29] GB/T,6394-2017,金属平均晶粒度测定法[S].