形核是自然界中最常见的相变现象之一，如蒸汽凝结、水结冰、矿物结晶等，同时还是工业生产中的重要控制环节，如生物制药、铸造、金属热处理等。因此，深入研究形核过程不仅有助于揭示相变机制，还具有重要的工业应用价值。然而，形核是一个发生在原子空间尺度及扩散时间尺度上的多尺度复杂问题，这导致实验上原位研究金属材料的形核过程依然面临较大困难。迄今为止，这一领域最重要的成果仍是20 世纪初提出的经典形核理论（Classical Nucleation Theory,CNT）及其修正模型。然而，由于CNT 对形核问题做了一系列简化，如单原子吸附、尖锐界面假设等，这使得CNT 不能定量描述临界相变点附近的形核过程[1]。近年来，研究人员为克服CNT 这一不足，进行了大量实验及模拟研究，发现晶体材料的结晶过程往往会经历一些中间态[2-4]，如高密度区域、非晶、亚稳晶体等，并提出中间相类型对形核率及形核路径具有重要影响。目前这类形核过程被统称为非经典形核或分步形核（Two-step nucleation,TS）。通常采用奥斯特瓦尔德的分步相变理论来解释分步形核问题，即形核过程首先形成与母相结构、能量相近的中间相，进而转变为晶体相。Guo 等[5]通过计算研究证实，中间相的存在往往可以降低形核势垒、促进形核。虽然TS 的一般机制已达成共识，并认为符合奥斯特瓦尔德的分步原则，但我们对晶体材料分步形核过程中的结构转变路径、中间相类型以及物性参数（如温度、浓度等）对形核动力学影响的认识仍然不足。
形核发生在原子尺度上，对CNT 和TS 机制的深入了解需要实验和数值模拟工作来提供形核过程的原子图像。对于真实的分子、原子体系，形核具有位置随机性、孕育时间长、存在时间短的特点，这导致采用实验方法原位观察形核过程仍然十分困难。所幸，随着计算机技术及数值方法的不断发展，仿真技术被广泛接受为除理论及实验手段外的第3种科学研究方法。其中，分子动力学[6]（MD）和动力学蒙特卡洛方法[7](KMC)是形核研究中常用的数值方法。MD 是一种基于牛顿力学理论的动力学方法，在形核路径研究上揭示了众多新机制，由于其模拟时间尺度在皮秒级，适用于大过冷或异质形核过程研究；KMC 是一种统计学方法，计算得到的形核率与实验值较吻合，然而，该方法不能正确处理界面扩散、界面形核等问题，不适合研究形核动力学路径。综上所述，虽然数值模拟工作给形核研究带来了一些新认识，由于方法缺陷的存在，分步形核机制仍未得到彻底揭示。
近年来，Elder 等[8]基于经典密度泛函理论提出了一种能够描述原子空间尺度及扩散时间尺度现象的新模型，晶体相场模型（Phase Field Crystal Model,PFC）。Voigt[9]采用单模PFC 研究了形核的最小能量路径；Guo 等[10]模拟了经典形核中的团簇涨落过程；Tóth 等[11]采用PFC 模拟了三维BCC 相的分步形核过程；最近，Guo 等[5,12]采用双模XPFC 研究了二维四方相形核的动力学路径。这些前期工作充分表明PFC 适合研究形核问题，因此，进一步采用该模型研究不同结构晶体相的形核路径以及不同物性参数下的形核过程能够给形核研究带来新的认识。本文作者将采用晶体相场模型，研究二维三角晶体相的形核过程，明确其形核路径，并考察温度、密度等物性参数对形核过程的影响。
1 晶体相场模型
本文采用Elder 提出的单模近似晶体相场模型，其泛函形式为[13]：
式中，ψ 为原子数密度；ε 为与温度有关的参数。
动力学方程为：
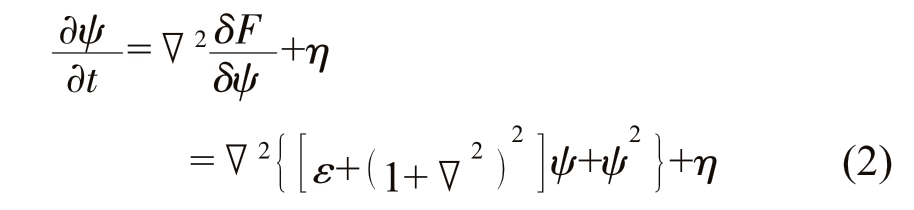
式中，t 是无量纲时间；η 是噪声。
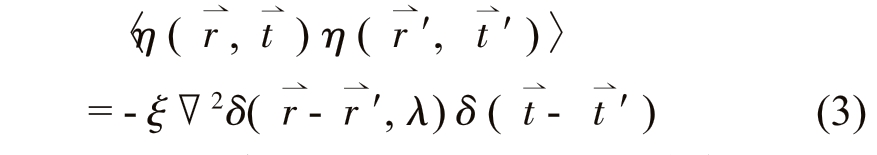
式中，ξ 为噪声强度，λ 为常量，取λ=a，其中a 为晶格常数。
时间步长Δt=0.5 ，空间步长Δx=Δy=π/4 ，模拟区域网格数为L×M=1 024×1 024，相参数取值在固液两相区内，这里温度取值范围为ε=[-0.3, -0.29]，初始密度取值范围为ψ=[0.31,0.32]，所有参数均为无量纲参数。
2 模拟结果与讨论
2.1 形核方式
过冷液相引入噪声后，系统内部开始形核，通过考察固液两相区（相图见文献[14]）内不同参数下的形核过程，发现二维三角晶体结构相结晶过程存在两种形核方式：单步形核和分步形核。单步形核过程为三角相核心直接在液相内部形成；而分步形核过程则是液相内部先出现高密度区域，而后三角晶核在高密度区域内部形成。其中，固相线附近以及低温条件下以分步形核为主，其它相区则以单步形核为主，这与胶体实验结果相一致[15]。
图1 为模拟得到的不同时刻模拟区域内某个晶粒单步形核过程的原子图像（图1a～1c）和横穿晶核直线上不同时刻的原子密度演化曲线（图1d～1f），相图参数取值在液相线附近为(ε,ψ)=(-0.3,0.32)。由图1a～1c 可知，形核过程表现为均匀液相内部直接出现具有三角点阵结构的短程有序团簇，这与经典单步形核理论相一致。而后，稳定晶核通过原子不断层层堆垛到短程有序团簇上得到，这表明经典形核理论中的单原子吸附脱附假设存在较大局限性。图1d～1f 中虚线峰为固相原子峰，本文定义振幅大于等于晶体原子振幅80%的密度峰（即图中虚线峰）代表固相原子，振幅小于晶体原子振幅50%的密度峰代表液相原子。通过考察密度峰演化过程，可清晰看到小团簇中心原子密度振幅已十分接近晶体相密度峰振幅，即形核过程是单步过程。进一步考察原子密度曲线发现，固液界面厚度约为2 个原子直径，表明纳米尺度晶核团簇的热力学性质应由界面主导，与宏观晶体相的热力学性质具有显著差异。因而，经典形核热力学采用尖锐界面假设及宏观热力学条件处理形核过程存在较大误差，仍需要进一步对经典模型进行修正。
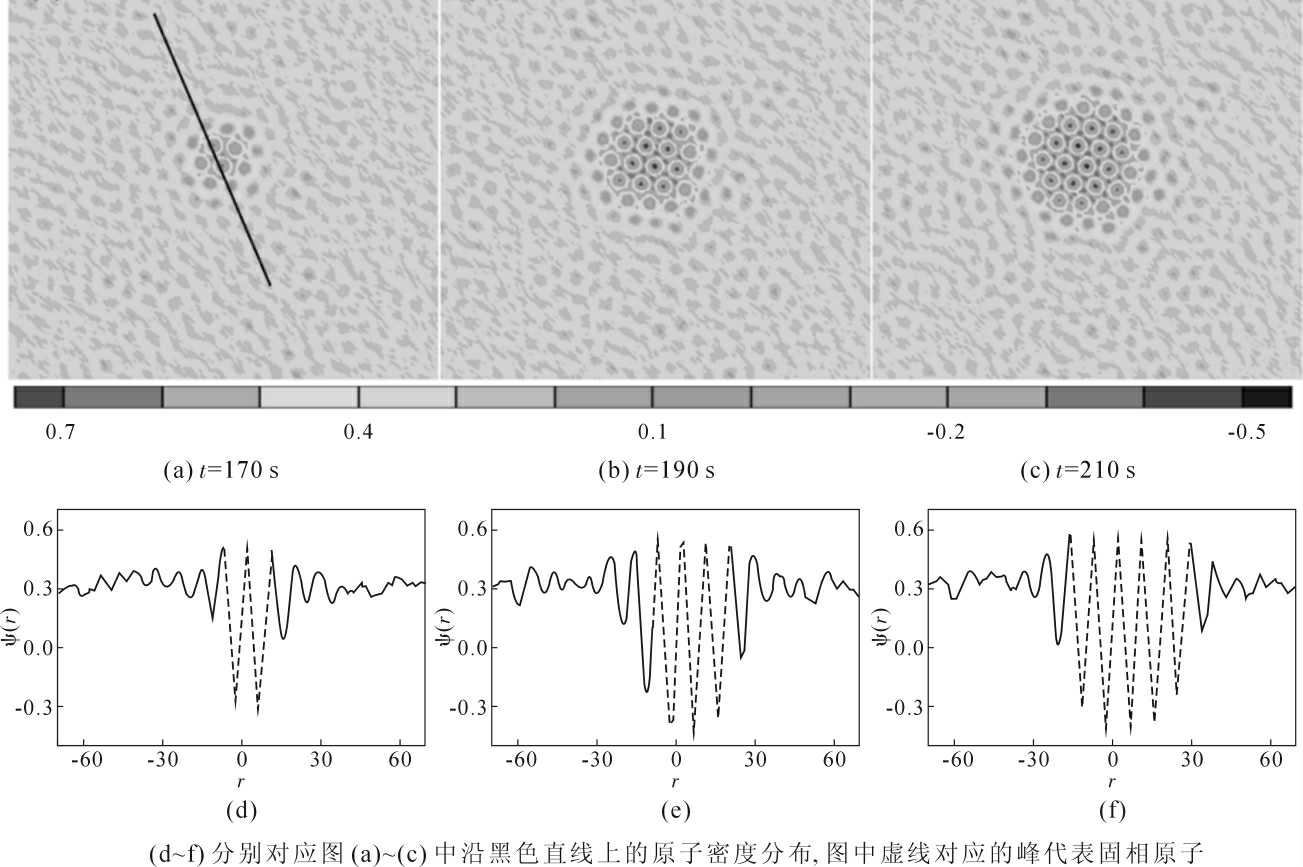
图1 经典单步形核过程的原子图像及穿越晶核某一直线上的原子密度曲线
Fig.1 Temporal evolution process of nucleation and density filed for classical one-step nucleation
图2为模拟得到的不同时刻分步形核过程的原子图像（图2a～2d）和穿过晶核方向上不同时刻的原子密度演化曲线（图2e～2h），图中虚线密度峰代表固相原子，(e),(f)虚线密度峰振幅介于固相与液相之间并具有短程有序特点，该类密度峰代表亚稳相，相图参数取值在固相线附近为(ε,ψ)=(-0.3,0.31)。由图2a～2d 可知，与单步形核过程相似，液相中首先出现具有三角晶格类型的短程有序小团簇，进而通过原子层层堆垛长大完成形核过程。然而，通过考察密度场演化曲线，发现二者形核过程具有本质区别。分步形核过程首先出现类晶体相亚稳团簇，其密度值介于液相与晶体相之间（见图2e、2f 虚线峰）；而后高密度区域内部出现晶体原子（图2g 虚线峰）；最终亚稳相完全转变为稳定相（见图2h）。这一形核过程已被胶体实验[3]及蛋白质结晶[16]实验所证实。此外，模拟结果表明，亚稳团簇并非完全无序的高密度液相或非晶相，其原子排列具有一定周期性，这与最新的实验及模拟结果相吻合[4,5]。
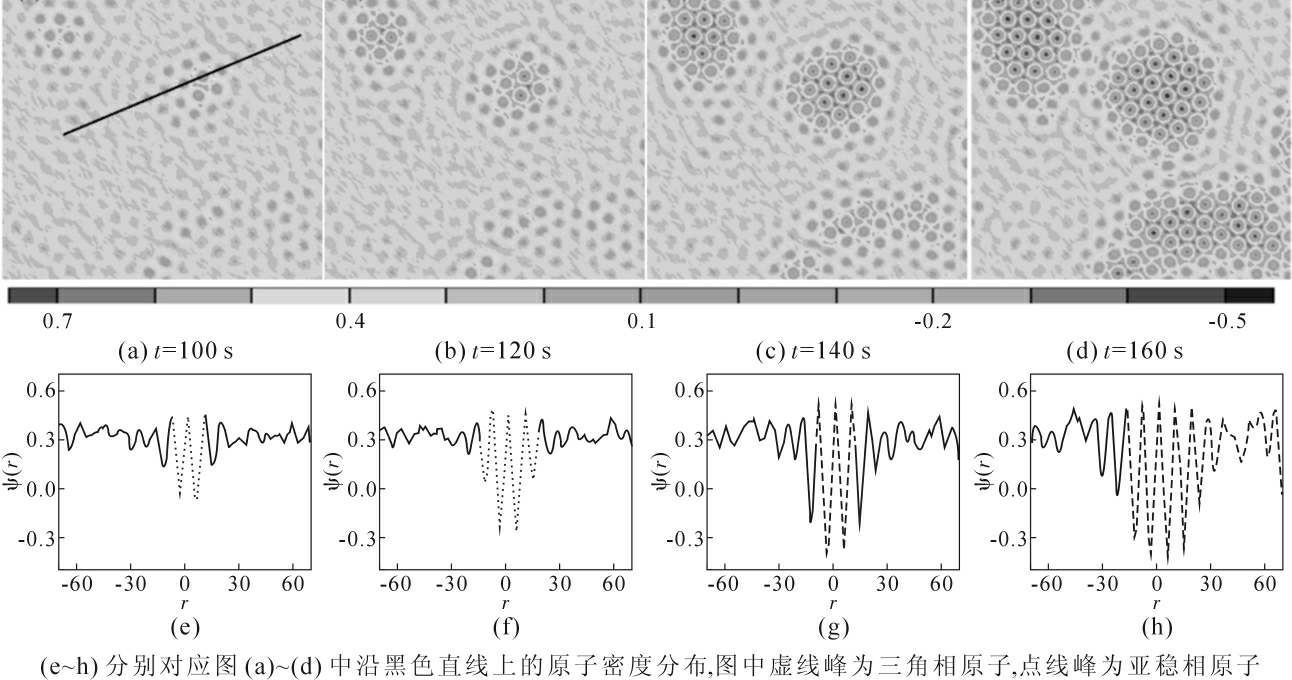
图2 分步形核过程的原子图像及穿越晶核某一直线上的原子密度曲线
Fig.2 Temporal evolution process of nucleation and density filed for nonclassical nucleation
2.2 初始密度对形核过程的影响
图3 给出了相同温度参数、不同初始密度条件下的形核过程以及后续结晶过程的原子图像，温度参数为ε=-0.3，初始密度分别为0.31（图3a）、0.315（图3b）、0.32（图3c）。由图可得，初始密度越小，形核越容易，晶核个数越多。参考相图可知，固相线在低密度区域，此时相变驱动力较大[10]，故而形核容易发生。进一步观察不同参数下的晶核形貌发现，晶核形貌往往并不规则。低密度条件下结晶驱动力较大，相变过程受界面动力学控制[17]，此时固液界面较弥散，扰动存在时固液界面将变得凹凸不平并容易出现多晶结构（见图3a）。高密度条件下相变受扩散过程控制[18]，此时界面能影响晶核形貌，晶核表面被高密排面包裹（见图1、图3c）。对于三角晶体不同密度下形核方式的差异是源于生长动力学及界面形貌的不同，低密度条件结晶驱动力大倾向于先形成有序亚稳团簇，进而通过密度扩散转变为稳态三角晶体，高密度扩散控制条件下则倾向于直接形成三角晶核。
图3 相同温度不同初始密度条件下的形核过程
Fig.3 Snapshots of atomic configurations during nucleation process with different initial atom number densities
为了量化初始密度对形核过程的影响，进一步统计了不同初始密度条件下的形核率和形核孕育时间，为了降低统计误差每个数据点均是5 组模拟结果的平均值，结果见图4。由图4(a)可得知，随着初始密度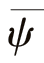
的增大，形核率不断减小。这源于两方面因素的影响：①小密度条件下相变驱动力较大，故而形核率大；②小密度条件下形核以分步形核为主，大量研究表明[15,19-20]中间相的存在能够有效降低形核能垒，进而导致形核率增大。图4(b)则为形核孕育时间与初始密度关系曲线，由图可知孕育时间随密度的增大而增加。
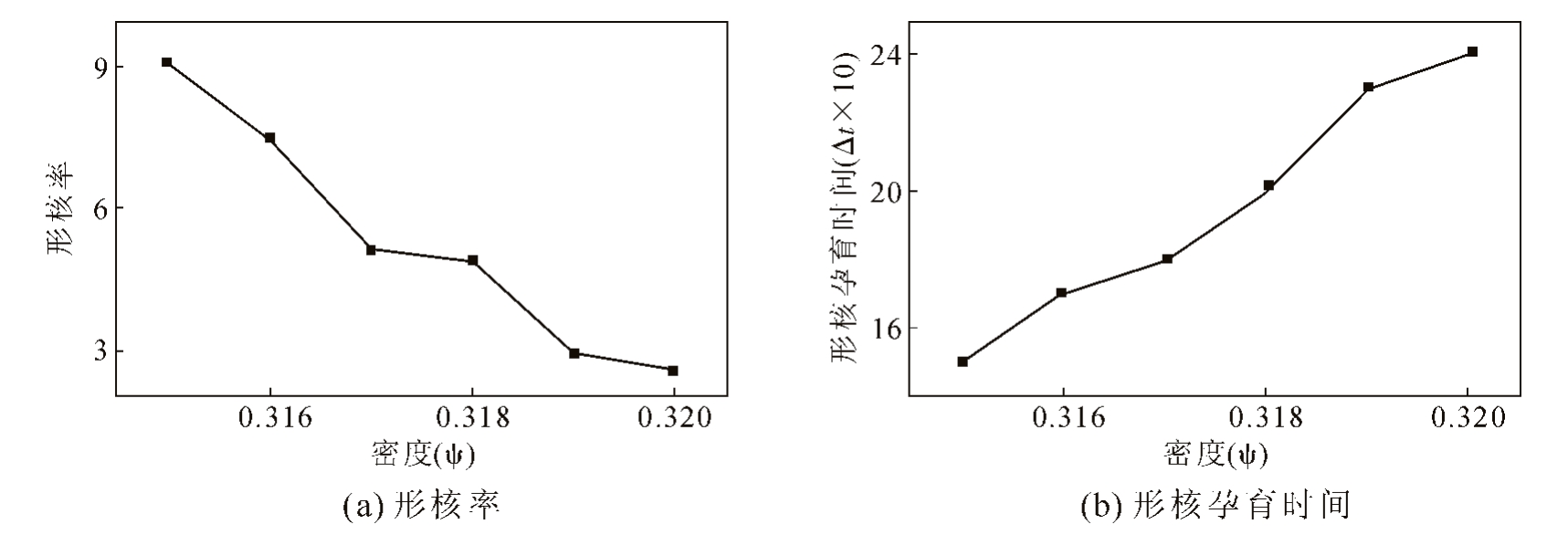
图4 相同温度参数不同密度条件下形核率与形核孕育时间变化曲线
Fig.4 The nucleation rate and incubation time with different initial densities
2.3 温度对形核过程的影响
温度是影响形核过程的重要物理变量之一，本节固定初始密度为0.315，温度参数取值范围为-0.30（固相线温度）到-0.25（液相线温度）。统计模拟结果发现，当温度参数大于-0.29 时，形核孕育时间很长，不能有效研究形核过程，因此这里重点研究了温度在-0.30 到-0.29 的形核行为。同时为了降低统计误差，每个数据点为5 组结果的统计平均值。模拟结果表明，温度对形核过程的影响与密度对形核过程的影响类似，原子图像可参考图3 而不再进一步给出，具体表现为随着温度参数降低，形核孕育时间减少，形核率越大，形核率及孕育时间随温度变化曲线见图5。由图5(a)可知，在两相区内随着温度参数降低，形核率逐渐增大，这与经典形核理论结论相符合，随着温度进一步降低，形核率将不再增大，这是由于较大过冷条件下原子扩散速率降低所致。此外，对晶核形貌及形核方式的影响上与初始密度值对其的影响相似，即低温条件下固液界面更为弥散，形核以分步形核为主；高温条件下固液界面接近尖锐界面，晶核表面被高密排面包裹，此时形核以单步形核为主。Tan 和Tang 等研究了三维FCC及二维四方相的形核过程[4-5, 21]，提出温度主要通过影响液态金属结构来影响形核动力学路径。本文模拟结果表明，对于三角晶核温度是通过影响界面性质来影响形核过程，这一结论与Tan 等人的研究结果并不矛盾，这是由于三角结构较FCC 及四方结构更为简单，温度对其液态结构影响并不显著所致[22]。
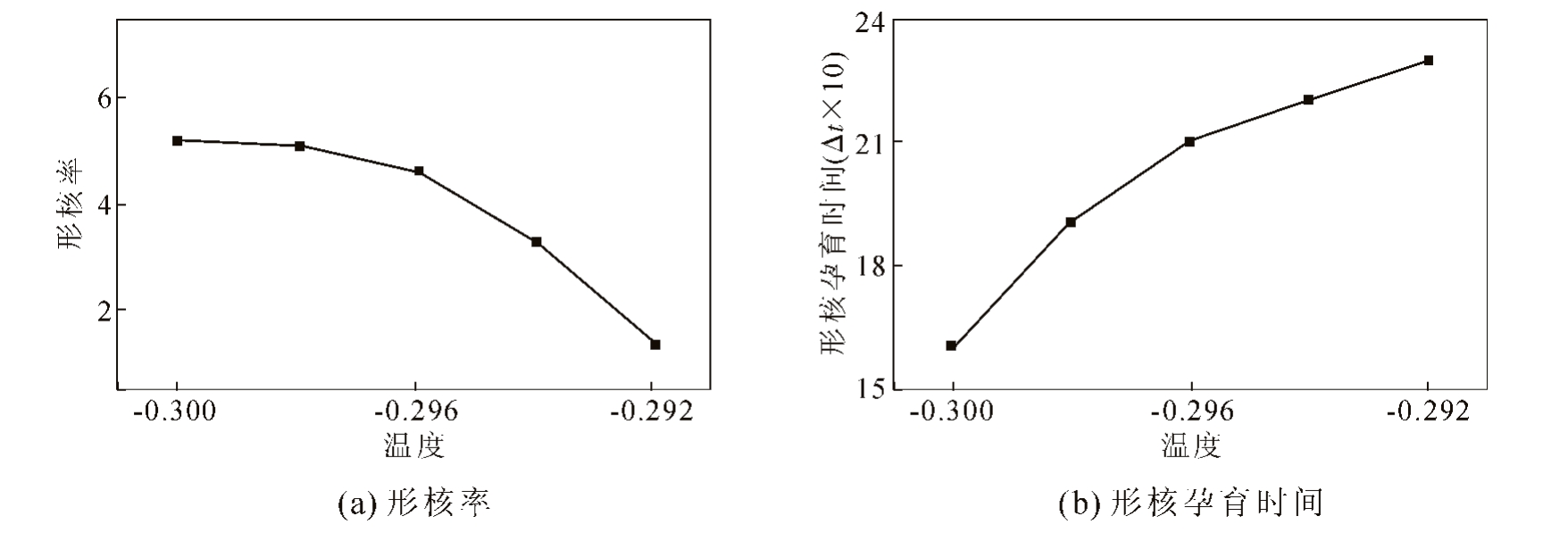
图5 相同密度不同温度参数条件下的形核率及形核孕育时间变化曲线
Fig.5 The curves of nucleation rate and incubation time under the same density and different temperature parameters
3 结论
采用晶体相场模型，模拟了二维三角晶体的形核过程，重点研究了初始密度、温度参数对形核方式、孕育时间及形核率的影响。
（1）发现三角晶体存在两种形核方式：单步形核和分步形核。单步形核过程为固相核心直接在液相内部形成；而分步形核过程则是液相内部先出现高密度区域，而后三角晶核在高密度区域内部形成。其中，低初始密度及低温条件下以分步形核为主，其它相区则以单步形核为主。
（2）对于简单三角结构晶体，初始密度与温度参数都是通过影响生长动力学及界面性质来影响形核方式和晶核形貌。
（3）进一步统计了不同初始密度及温度参数下的形核率和形核孕育时间，发现形核率随着温度降低而增大，形核孕育时间则随温度降低不断减小；随着密度增大形核率不断减小，而形核孕育时间则不断增大。
（4）通过考察晶核演化过程，发现较小密度及较低温度条件容易形核主要是源于两方面因素：一是该类条件下形核为分步形核，中间相的存在有助于降低形核能垒促进形核过程的发生；二是该类条件下相变驱动力大有利于形核。
[1] KELTON K,GREER A L.Nucleation in condensed matter: applications in materials and biology[M].Elsevier,2010.
[2] ZHANG K Q,LIU X Y.In situ observation of colloidal monolayer nucleation driven by an alternating electric field [J].Nature,2004,429(6993):739-743.
[3] ZHANG T H,LIU X Y.How Does a Transient Amorphous Precursor Template Crystallization[J].journal of the American Chemical Society,2007,129(44):13520-13526.
[4] TAN P, XU N, XU L. Visualizing kinetic pathways of homogeneous nucleation in colloidal crystallization[J]. Nature Physics,2014,10(1):73-79.
[5] GUO C,WANG J,LI J,et al.Kinetic Pathways and Mechanisms of Two-Step Nucleation in Crystallization[J]. Journal of Physical Chemistry Letters,2016,7(5008-14).
[6] SHIBUTA Y,SAKANE S,MIYOSHI E,et al.Heterogeneity in homogeneous nucleation from billion-atom molecular dynamics simulation of solidification of pure metal[J].Nature Communications,2017,8(10):17-21.
[7] STAUFFER D, CONIGLIO A, HEERMANN D W. Monte-carlo experiment for nucleation rate in the three-dimensional Ising model[J].Physical Review Letters,1982,49(18):1299-1302.
[8] ELDER K R, PROVATAS N, BERRY J, et al. Phase-field crystal modeling and classical density functional theory of freezing[J].Physical Review B,2007,75(6):064107.
[9] BACKOFEN R,RA¨TZ A,VOIGT A.Nucleation and growth by a phase field crystal (PFC) model[J].Philosophical Magazine Letters,2007,87(11):813-820.
[10] GUO C, WANG J, WANG Z, et al. Interfacial free energy adjustable phase field crystal model for homogeneous nucleation[J].Soft matter,2016,12(20):4666-4673.
[11] TÓTH G I, PUSZTAI T, TEGZE G, et al. Amorphous nucleation precursor in highly nonequilibrium fluids[J].Physical Review Letters,2011,107(17):175702.
[12] GUO C,WANG J,LI J,et al.Coupling eutectic nucleation mechanism investigated by phase field crystal model[J].Acta Materialia,2018,145:175-185.
[13] ELDER K R, KATAKOWSKI M, HAATAJA M, et al. Modeling elasticity in crystal growth[J]. Physical Review Letters, 2002, 88(24):245701.
[14] TANG S,YU Y M,WANG J,et al. Phase-field-crystal simulation of nonequilibrium crystal growth[J].Physical Review E,2014,89(1):012405.
[15] SAVAGE J R, DINSMORE A D. Experimental evidence for two-Step nucleation in colloidal crystallization[J].Physical Review Letters,2009,102(19):198302.
[16] SAUTER A,ROOSEN-RUNGE F,ZHANG F,et al.Real-time observation of nonclassical protein crystallization kinetics [J].Jour nal of the American Chemical Society, 2015, 137 (4):1485-1491.
[17] TANG S,YU Y-M,WANG J,et al.Phase-field-crystal simulation of nonequilibrium crystal growth [J].Physical Review E,2014,89(1):012405.
[18] GUO C, WANG J, WANG Z, et al. Modified phase-field-crystal model for solid-liquid phase transitions[J]. Physical Review E,2015,92(1):013309.
[19] GUO C,WANG J C,WANG Z J,et al.Atomistic investigation of homogeneous nucleation in undercooled liquid [J].Philosophical Magazine,2017,97(26):2255-2267.
[20] ERDEMIR D, LEE A Y, MYERSON A S. Nucleation of Crystals from Solution: Classical and Two-Step Models[J]. Accounts of Chemical Research,2009,42(5):621-629.
[21] TANG S, WANG J C, SVENDSEN B, et al. Competitive bcc and fcc crystal nucleation from non-equilibrium liquids studied by phase-field crystal simulation [J]. Acta Materialia, 2017, 139:196-204.
[22] 郭灿，王志军，王锦程，等.直接相关函数对双模晶体相场模型相图的影响[J].物理学报,2013,62(10):108104.